Week 5: Emukit and Experimental Design

[jupyter][google colab][reveal]

Neil D. Lawrence

Abstract:

We have introduced you to the sequential process by which we decide to evaluation points in a simulation through Bayesian optimization. In this lecture we introduce Emukit. Emukit is a software framework for decision programming via surrogate modelling and emulation. It formalizes the process of selecting a point via an acquisition function and provides a general framework for incorporating surrogate models and the acquisition function of your choice. We’ll then show how Emukit can be used for active experimental design.

Setup

notutils

This small package is a helper package for various notebook utilities used below.

The software can be installed using

%pip install notutils

from the command prompt where you can access your python installation.

The code is also available on GitHub: https://github.com/lawrennd/notutils

Once notutils is installed, it can be imported in the usual manner.

import notutils

pods

In Sheffield we created a suite of software tools for ‘Open Data Science’. Open data science is an approach to sharing code, models and data that should make it easier for companies, health professionals and scientists to gain access to data science techniques.

You can also check this blog post on Open Data Science.

The software can be installed using

%pip install pods

from the command prompt where you can access your python installation.

The code is also available on GitHub: https://github.com/lawrennd/ods

Once pods is installed, it can be imported in the usual manner.

import pods

mlai

The mlai software is a suite of helper functions for teaching and demonstrating machine learning algorithms. It was first used in the Machine Learning and Adaptive Intelligence course in Sheffield in 2013.

The software can be installed using

%pip install mlai

from the command prompt where you can access your python installation.

The code is also available on GitHub: https://github.com/lawrennd/mlai

Once mlai is installed, it can be imported in the usual manner.

import mlai
from mlai import plot

%pip install gpy

%pip install pyDOE

%pip install emukit

Simulation System

An example of a complex decision-making system might be a climate model, in such a system there are separate models for the atmosphere, the ocean and the land.

The components of these systems include flowing of currents, chemical interactions in the upper atmosphere, evaporation of water etc..

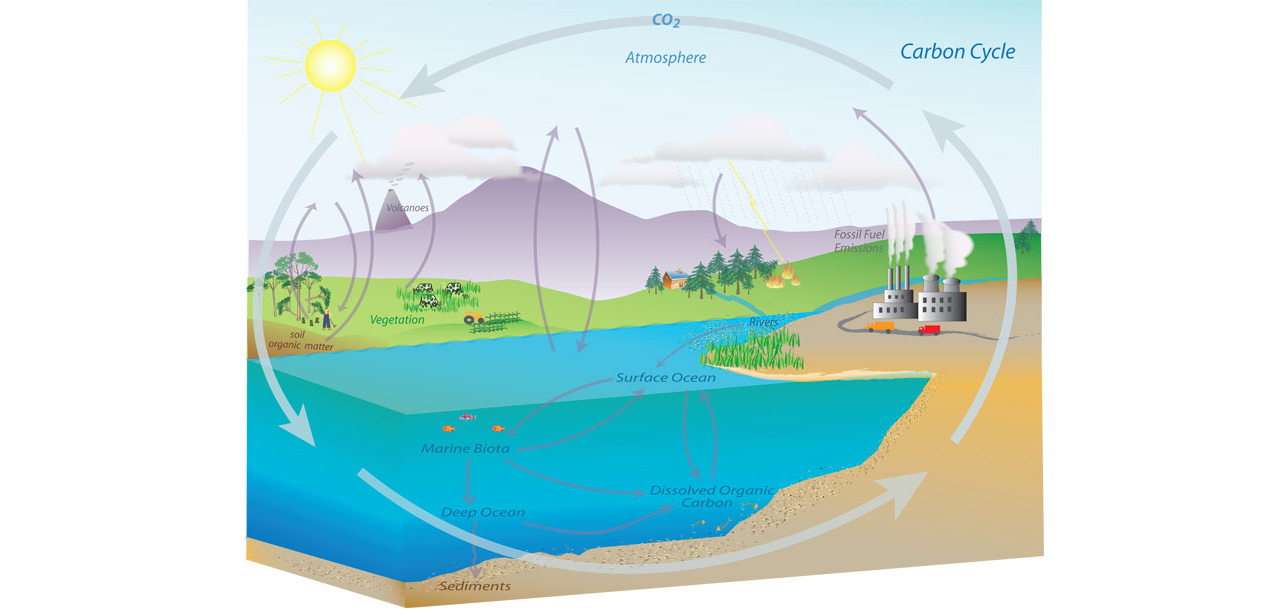
Figure: Representation of the Carbon Cycle from the US National Oceanic and Atmospheric Administration. While everything is interconnected in the system, we can decompose into separate models for atmosphere, ocean, land.

The influence of human activity also needs to be incorporated and modelled so we can make judgments about how to mitigate the effects of global warming.

Figure: The components of a simulation system for climate modelling.

Monolithic System

The classical approach to building these systems was a ‘monolithic system’. Built in a similar way to the successful applications software such as Excel or Word, or large operating systems, a single code base was constructed. The complexity of such code bases run to many lines.

In practice, shared dynamically linked libraries may be used for aspects such as user interface, or networking, but the software often has many millions of lines of code. For example, the Microsoft Office suite is said to contain over 30 million lines of code.

Figure: A potential path of models in a machine learning system.

Service Oriented Architecture

Such software is not only difficult to develop, but also to scale when computation demands increase. For example, Amazon’s original website software (called Obidos) was a monolithic design but by the early noughties it was becoming difficult to sustain and maintain. The software was phased out in 2006 to be replaced by a modularized software known as a ‘service-oriented architecture’.

In Service Oriented Architecture, or “Software as a Service” the idea is that code bases are modularized and communicate with one another using network requests. A standard approach is to use a REST API. So, rather than a single monolithic code base, the code is developed with individual services that handle the different requests.

The simulation software is turned inside out to expose the individual components to the operator.

Figure: A potential path of models in a machine learning system.

This is the landscape we now find ourselves in for software development. In practice, each of these services is often ‘owned’ and maintained by an individual team. The team is judged by the quality of their service provision. They work to detailed specifications on what their service should output, what its availability should be and other objectives like speed of response. This allows for conditional independence between teams and for faster development.

One question is to what extent is the same approach possible/desirable for scientific models? The components we listed above are already separated and often run independently. But those components themselves are made up of other sub-components that could also be exposed in a similar manner to software-as-a-service, giving us the notion of “simulation as a service”.

One thing about working in an industrial environment, is the way that short-term thinking actions become important. For example, in Formula One, the teams are working on a two-week cycle to digest information from the previous week’s race and incorporate updates to the car or their strategy.

However, businesses must also think about more medium-term horizons. For example, in Formula 1 you need to worry about next year’s car. So, while you’re working on updating this year’s car, you also need to think about what will happen for next year and prioritize these conflicting needs appropriately.

In the Amazon supply chain, there are equivalent demands. If we accept that an artificial intelligence is just an automated decision-making system. And if we measure in terms of money automatically spent, or goods automatically moved, then Amazon’s buying system is perhaps the world’s largest AI.

Those decisions are being made on short time schedules; purchases are made by the system on weekly cycles. But just as in Formula 1, there is also a need to think about what needs to be done next month, next quarter and next year. Planning meetings are held not only on a weekly basis (known as weekly business reviews), but monthly, quarterly, and then yearly meetings for planning spends and investments.

Amazon is known for being longer term thinking than many companies, and a lot of this is coming from the CEO. One quote from Jeff Bezos that stuck with me was the following.

“I very frequently get the question: ‘What’s going to change in the next 10 years?’ And that is a very interesting question; it’s a very common one. I almost never get the question: ‘What’s not going to change in the next 10 years?’ And I submit to you that that second question is actually the more important of the two – because you can build a business strategy around the things that are stable in time. … [I]n our retail business, we know that customers want low prices, and I know that’s going to be true 10 years from now. They want fast delivery; they want vast selection. It’s impossible to imagine a future 10 years from now where a customer comes up and says, ‘Jeff I love Amazon; I just wish the prices were a little higher,’ [or] ‘I love Amazon; I just wish you’d deliver a little more slowly.’ Impossible. And so the effort we put into those things, spinning those things up, we know the energy we put into it today will still be paying off dividends for our customers 10 years from now. When you have something that you know is true, even over the long term, you can afford to put a lot of energy into it.”

This quote is incredibly important for long term thinking. Indeed, it’s a failure of many of our simulations that they focus on what is going to happen, not what will not happen. In Amazon, this meant that there was constant focus on these three areas, keeping costs low, making delivery fast and improving selection. For example, shortly before I left Amazon moved its entire US network from two-day delivery to one-day delivery. This involves changing the way the entire buying system operates. Or, more recently, the company has had to radically change the portfolio of products it buys in the face of Covid19.

Figure: Experiment, analyze and design is a flywheel of knowledge that is the dual of the model, data and compute. By running through this spiral, we refine our hypothesis/model and develop new experiments which can be analyzed to further refine our hypothesis.

From the perspective of the team that we had in the supply chain, we looked at what we most needed to focus on. Amazon moves very quickly, but we could also take a leaf out of Jeff’s book, and instead of worrying about what was going to change, remember what wasn’t going to change.

We don’t know what science we’ll want to do in five years’ time, but we won’t want slower experiments, we won’t want more expensive experiments and we won’t want a narrower selection of experiments.

As a result, our focus was on how to speed up the process of experiments, increase the diversity of experiments that we can do, and keep the experiments price as low as possible.

The faster the innovation flywheel can be iterated, then the quicker we can ask about different parts of the supply chain, and the better we can tailor systems to answering those questions.

We need faster, cheaper and more diverse experiments which implies we need better ecosystems for experimentation. This has led us to focus on the software frameworks we’re using to develop machine learning systems including data oriented architectures (Borchert (2020);Lawrence (2019);Vorhemus and Schikuta (2017);Joshi (2007)), data maturity assessments (Lawrence et al. (2020)) and data readiness levels (See this blog post on Data Readiness Levels. and Lawrence (2017);The DELVE Initiative (2020))

Packing Problems

Figure: Packing 9 squares into a single square. This example is trivially solved. Credit https://erich-friedman.github.io/packing/

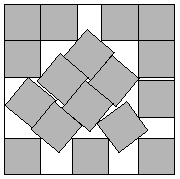
Figure: Packing 17 squares into a single square. The optimal solution is sometimes hard to find. Here the side length of the smallest square that holds 17 similarly shaped squares is at least 4.675 times the smaller square. This solution found by John Bidwell in 1997. Credit https://erich-friedman.github.io/packing/

Another example of a problem where the “physics” is understood because it’s really mathematics, is packing problems. Here the mathematics is just geometry, but still we need some form of compute to solve these problems. Erich Friedman’s website contains a host of these problems, only some of which are analytically tractable.

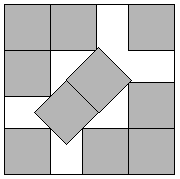
Figure: Packing 10 squares into a single square. This example is proven by Walter Stromquist (Stromquist, 1984). Here \(s=3+\frac{1}{\sqrt{2}}\). Credit https://erich-friedman.github.io/packing/

Modelling with a Function

What if the question of interest was quite simple, for example in the packing problem, we just wanted to know the minimum side length. Sometimes, regardless of the complexity of the problem, there can be a pattern to the answer that is emergent due to regularities in the underlying problem.

Erich Friedman Packing Data

import numpy as np
import pods

data = pods.datasets.erich_friedman_packing_data()
x = data['X']
y = data['Y']

Figure: Plot of minimum side length known as a function of number of squares inside.

Gaussian Process Fit

Our first objective will be to perform a Gaussian process fit to the data, we’ll do this using the GPy software.

import GPy

m_full = GPy.models.GPRegression(x,y)
_ = m_full.optimize() # Optimize parameters of covariance function

The first command sets up the model, then m_full.optimize() optimizes the parameters of the covariance function and the noise level of the model. Once the fit is complete, we’ll try creating some test points, and computing the output of the GP model in terms of the mean and standard deviation of the posterior functions between 1870 and 2030. We plot the mean function and the standard deviation at 200 locations. We can obtain the predictions using y_mean, y_var = m_full.predict(xt)

xt = np.linspace(0,100,400)[:,np.newaxis]
yt_mean, yt_var = m_full.predict(xt)
yt_sd=np.sqrt(yt_var)

Now we plot the results using the helper function in mlai.plot.

Figure: Gaussian process fit to the Erich Friedman Packing data.

Statistical Emulation

Figure: The UK Met office runs a shared code base for its simulations of climate and the weather. This plot shows the different spatial and temporal scales used.

In many real-world systems, decisions are made through simulating the environment. Simulations may operate at different granularities. For example, simulations are used in weather forecasts and climate forecasts. Interestingly, the UK Met office uses the same code for both, it has a “Unified Model” approach, but they operate climate simulations at greater spatial and temporal resolutions.

Figure: Real world systems consist of simulators that capture our domain knowledge about how our systems operate. Different simulators run at different speeds and granularities.

Figure: A statistical emulator is a system that reconstructs the simulation with a statistical model.

A statistical emulator is a data-driven model that learns about the underlying simulation. Importantly, learns with uncertainty, so it ‘knows what it doesn’t know’. In practice, we can call the emulator in place of the simulator. If the emulator ‘doesn’t know’, it can call the simulator for the answer.

Figure: A statistical emulator is a system that reconstructs the simulation with a statistical model. As well as reconstructing the simulation, a statistical emulator can be used to correlate with the real world.

As well as reconstructing an individual simulator, the emulator can calibrate the simulation to the real world, by monitoring differences between the simulator and real data. This allows the emulator to characterize where the simulation can be relied on, i.e., we can validate the simulator.

Similarly, the emulator can adjudicate between simulations. This is known as multi-fidelity emulation. The emulator characterizes which emulations perform well where.

If all this modelling is done with judicious handling of the uncertainty, the computational doubt, then the emulator can assist in deciding what experiment should be run next to aid a decision: should we run a simulator, in which case which one, or should we attempt to acquire data from a real-world intervention.

GPy: A Gaussian Process Framework in Python

Gaussian processes are a flexible tool for non-parametric analysis with uncertainty. The GPy software was started in Sheffield to provide a easy to use interface to GPs. One which allowed the user to focus on the modelling rather than the mathematics.

Figure: GPy is a BSD licensed software code base for implementing Gaussian process models in Python. It is designed for teaching and modelling. We welcome contributions which can be made through the GitHub repository https://github.com/SheffieldML/GPy

GPy is a BSD licensed software code base for implementing Gaussian process models in python. This allows GPs to be combined with a wide variety of software libraries.

The software itself is available on GitHub and the team welcomes contributions.

The aim for GPy is to be a probabilistic-style programming language, i.e., you specify the model rather than the algorithm. As well as a large range of covariance functions the software allows for non-Gaussian likelihoods, multivariate outputs, dimensionality reduction and approximations for larger data sets.

The documentation for GPy can be found here.

GPy Tutorial

This GPy tutorial is based on material we share in the Gaussian process summer school for teaching these models https://gpss.cc. It contains material from various members and former members of the Sheffield machine learning group, but particular mention should be made of Nicolas Durrande and James Hensman, see http://gpss.cc/gpss17/labs/GPSS_Lab1_2017.ipynb.

import numpy as np
import GPy

To give a feel for the software we’ll start by creating an exponentiated quadratic covariance function, \[ k(\mathbf{ x}, \mathbf{ x}^\prime) = \alpha \exp\left(-\frac{\left\Vert \mathbf{ x}- \mathbf{ x}^\prime \right\Vert_2^2}{2\ell^2}\right), \] where the length scale is \(\ell\) and the variance is \(\alpha\).

To set this up in GPy we create a kernel in the following manner.

input_dim=1
alpha = 1.0
lengthscale = 2.0
kern = GPy.kern.RBF(input_dim=input_dim, variance=alpha, lengthscale=lengthscale)

That builds a kernel object for us. The kernel can be displayed.

display(kern)

Or because it’s one dimensional, you can also plot the kernel as a function of its inputs (while the other is fixed).

Figure: The exponentiated quadratic covariance function as plotted by the GPy.kern.plot command.

You can set the length scale of the covariance to different values and plot the result.

kern = GPy.kern.RBF(input_dim=input_dim)     # By default, the parameters are set to 1.
lengthscales = np.asarray([0.2,0.5,1.,2.,4.])

Figure: The exponentiated quadratic covariance function plotted for different length scales by GPy.kern.plot command.

Covariance Functions in GPy

Many covariance functions are already implemented in GPy. Instead of rbf, try constructing and plotting the following covariance functions: exponential, Matern32, Matern52, Brownian, linear, bias, rbfcos, periodic_Matern32, etc. Some of these covariance functions, such as rbfcos, are not parametrized by a variance and a length scale. Further, not all kernels are stationary (i.e., they can’t all be written as \(k(\mathbf{ x}, \mathbf{ x}^\prime) = f(\mathbf{ x}-\mathbf{ x}^\prime)\), see for example the Brownian covariance function). So for plotting it may be interesting to change the value of the fixed input.

Combining Covariance Functions in GPy

In GPy you can easily combine covariance functions you have created using the sum and product operators, + and *. So, for example, if we wish to combine an exponentiated quadratic covariance with a Matern 5/2 then we can write

kern1 = GPy.kern.RBF(1, variance=1., lengthscale=2.)
kern2 = GPy.kern.Matern52(1, variance=2., lengthscale=4.)
kern = kern1 + kern2
display(kern)

Figure: A combination of the exponentiated quadratic covariance plus the Matern \(5/2\) covariance.

Or if we wanted to multiply them, we can write

kern1 = GPy.kern.RBF(1, variance=1., lengthscale=2.)
kern2 = GPy.kern.Matern52(1, variance=2., lengthscale=4.)
kern = kern1 * kern2
display(kern)

Figure: A combination of the exponentiated quadratic covariance multiplied by the Matern \(5/2\) covariance.

You can learn about how to implement new kernel objects in GPy here.

Figure: Designing the covariance function for your Gaussian process is a key place in which you introduce your understanding of the data problem. To learn more about the design of covariance functions, see this talk from Nicolas Durrande at GPSS in 2016.

A Gaussian Process Regression Model

We will now combine the Gaussian process prior with some data to form a GP regression model with GPy. We will generate data from the function \[ f( x) = − \cos(\pi x) + \sin(4\pi x) \] over the domain \([0, 1]\), adding some noise to gives \[ y(x) = f(x) + \epsilon, \] with the noise being Gaussian distributed, \(\epsilon\sim \mathcal{N}\left(0,0.01\right)\).

X = np.linspace(0.05,0.95,10)[:,np.newaxis]
Y = -np.cos(np.pi*X) + np.sin(4*np.pi*X) + np.random.normal(loc=0.0, scale=0.1, size=(10,1))

Figure: Data from the noisy sine wave for fitting with a GPy model.

A GP regression model based on an exponentiated quadratic covariance function can be defined by first defining a covariance function.

kern = GPy.kern.RBF(input_dim=1, variance=1., lengthscale=1.)

And then combining it with the data to form a Gaussian process model.

model = GPy.models.GPRegression(X,Y,kern)

Just as for the covariance function object, we can find out about the model using the command display(model).

display(model)

Note that by default the model includes some observation noise with variance 1. We can see the posterior mean prediction and visualize the marginal posterior variances using model.plot().

Figure: A Gaussian process fit to the noisy sine data. Here the parameters of the process and the covariance function haven’t yet been optimized.

You can also look directly at the predictions for the model using.

Xstar = np.linspace(0, 10, 100)[:, np.newaxis]
Ystar, Vstar = model.predict(Xstar)

Which gives you the mean (Ystar), the variance (Vstar) at the locations given by Xstar.

Covariance Function Parameter Estimation

As we have seen during the lectures, the parameters values can be estimated by maximizing the likelihood of the observations. Since we don’t want any of the variances to become negative during the optimization, we can constrain all parameters to be positive before running the optimization.

model.constrain_positive()

The warnings are because the parameters are already constrained by default, the software is warning us that they are being reconstrained.

Now we can optimize the model using the model.optimize() method. Here we switch messages on, which allows us to see the progression of the optimization.

model.optimize(messages=True)

By default, the optimization is using a limited memory BFGS optimizer (Byrd et al., 1995).

Once again, we can display the model, now to see how the parameters have changed.

display(model)

The length scale is much smaller, as well as the noise level. The variance of the exponentiated quadratic has also reduced.

Figure: A Gaussian process fit to the noisy sine data with parameters optimized.

GPy and Emulation

Let \(\mathbf{ x}\) be a random variable defined over the real numbers, \(\Re\), and \(f(\cdot)\) be a function mapping between the real numbers \(\Re \rightarrow \Re\).

The problem of uncertainty propagation is the study of the distribution of the random variable \(f(\mathbf{ x})\).

We’re going to address this problem using emulation and GPy. We will see in this section the advantage of using a model when only a few observations of \(f\) are available.

Firstly, we’ll make use of a test function known as the Branin test function. \[ f(\mathbf{ x}) = a(x_2 - bx_1^2 + cx_1 - r)^2 + s(1-t \cos(x_1)) + s \] where we are setting \(a=1\), \(b=5.1/(4\pi^2)\), \(c=5/\pi\), \(r=6\), \(s=10\) and \(t=1/(8\pi)\).

import numpy as np

def branin(X):
    y = ((X[:,1]-5.1/(4*np.pi**2)*X[:,0]**2+5*X[:,0]/np.pi-6)**2 
        + 10*(1-1/(8*np.pi))*np.cos(X[:,0])+10)
    return(y)

We’ll define a grid of twenty-five observations over [−5, 10] × [0, 15] and a set of 25 observations.

# Training set defined as a 5*5 grid:
xg1 = np.linspace(-5,10,5)
xg2 = np.linspace(0,15,5)
X = np.zeros((xg1.size * xg2.size,2))
for i,x1 in enumerate(xg1):
    for j,x2 in enumerate(xg2):
        X[i+xg1.size*j,:] = [x1,x2]

Y = branin(X)[:,np.newaxis]

The task here will be to consider the distribution of \(f(U)\), where \(U\) is a random variable with uniform distribution over the input space of \(f\). We focus on the computaiton of two quantities, the expectation of \(f(U)\), \(\left\langle f(U)\right\rangle\), and the probability that the value is greater than 200.

Computation of \(\left\langle f(U)\right\rangle\)

The expectation of \(f(U )\) is given by \(\int_\mathbf{ x}f( \mathbf{ x})\text{d}\mathbf{ x}\). A basic approach to approximate this integral is to compute the mean of the 25 observations: np.mean(Y). Since the points are distributed on a grid, this can be seen as the approximation of the integral by a rough Riemann sum.

print('Estimate of the expectation is given by: {mean}'.format(mean=Y.mean()))

The result can be compared with the actual mean of the Branin function which is 54.31.

Alternatively, we can fit a GP model and compute the integral of the best predictor by Monte Carlo sampling.

Firstly, we create the covariance function. Here we’re going to use an exponentiated quadratic, but we’ll augment it with the ‘bias’ covariance function. This covariance function represents a single fixed bias that is added to the overall covariance. It allows us to deal with non-zero-mean emulations.

import GPy

# Create an exponentiated quadratic plus bias covariance function
kern_eq = GPy.kern.RBF(input_dim=2, ARD = True)
kern_bias = GPy.kern.Bias(input_dim=2)
kern = kern_eq + kern_bias

Now we construct the Gaussian process regression model in GPy.

# Build a GP model
model = GPy.models.GPRegression(X,Y,kern)

In the sinusoid example above, we learnt the variance of the process. But in this example, we are fitting an emulator to a function we know is noise-free. However, we don’t fix the noise value to precisely zero, as this can lead to some numerical errors. Instead, we fix the variance of the Gaussian noise to a very small value.

# fix the noise variance
model.likelihood.variance.fix(1e-5)

Now we fit the model. Note, that the initial values for the length scale are not appropriate. So first set the length scale of the model needs to be reset.

kern.rbf.lengthscale = np.asarray([3, 3])

It’s a common error in Gaussian process fitting to initialize the length scale too small or too big. The challenge is that the error surface is normally multimodal, and the final solution can be very sensitive to this initialization. If the length scale is initialized too small, the solution can converge on an place where the signal isn’t extracted by the covariance function. If the length scale is initialized too large, then the variations of the function are often missing. Here the length scale is set for each dimension of inputs as 3. Now that’s done, we can optimize the model.

# Randomize the model and optimize
model.optimize(messages=True)

Figure: A Gaussian process fit to the Branin test function, used to assess the mean of the function by emulation.

Finally, we can compute the mean of the model predictions using very many Monte Carlo samples.

Note, that in this example, because we’re using a test function, we could simply have done the Monte Carlo estimation directly on the Branin function. However, imagine instead that we were trying to understand the results of a complex computational fluid dynamics simulation, where each run of the simulation (which is equivalent to our test function) took many hours. In that case the advantage of the emulator is clear.

# Compute the mean of model prediction on 1e5 Monte Carlo samples
Xp = np.random.uniform(size=(int(1e5),2))
Xp[:,0] = Xp[:,0]*15-5
Xp[:,1] = Xp[:,1]*15
mu, var = model.predict(Xp)
print('The estimate of the mean of the Branin function is {mean}'.format(mean=np.mean(mu)))

Exercise 1

Now think about how to make use of the variance estimation from the Gaussian process to obtain error bars around your estimate.

Exercise 2

You’ve seen how the Monte Carlo estimates work with the Gaussian process. Now make your estimate of the probability that the Branin function is greater than 200 with the uniform random inputs.

Uncertainty Quantification and Design of Experiments

We’re introducing you to the optimization and analysis of real-world models through emulation, a domain that is part of the broader field known as surrogate modelling. This involves creating simplified models that approximate more complex systems, allowing for efficient exploration and analysis.

Although we’re approaching this from the machine learning perspective, with a computer-scientist’s approach, you won’t be surprised to hear that this field is not new. There are diverse research communities, including statisticians and engineers, who have long been interested in these methods.

Our focus has been on active experimental design, where we sequentially select points to run our simulation based on previous results, optimizing the process iteratively.

Now, we pause to explore passive experimental design approaches. In passive design, we select initial points to ‘seed’ the emulator without running the simulator. This is crucial for setting up the emulator effectively.

The challenge of determining where to run simulations to obtain the necessary answers is longstanding. A seminal paper by McKay et al. (1979) reviews three foundational methods for designing these inputs: random sampling, stratified sampling, and Latin hypercube sampling. These methods provide structured ways to explore the input space and are essential for effective experimental design.

Random sampling is the default approach, where samples are selected randomly across the input domain of interest. This can be done uniformly or based on an assumed underlying distribution. It is straightforward but may not always provide comprehensive coverage of the input space.

Let the input values \(\mathbf{ x}_1, \dots, \mathbf{ x}_n\) be a random sample from \(f(\mathbf{ x})\). This method of sampling is perhaps the most obvious, and an entire body of statistical literature may be used in making inferences regarding the distribution of \(Y(t)\).

Stratified sampling involves dividing a population into sub-populations, or strata, before sampling. This ensures that all sub-populations are represented in the sample. For instance, in Covid-19 tracking, stratifying by age groups ensures coverage across all ages, which might be missed in simple random sampling.

In emulation, similar principles apply. The input domain can be divided into areas of particular interest. For example, when testing an F1 car component, you might focus on performance in different track sections, ensuring comprehensive data collection across varied conditions.

Using stratified sampling, all areas of the sample space of \(\mathbf{ x}\) are represented by input values. Let the sample space \(S\) of \(\mathbf{ x}\) be partitioned into \(I\) disjoint strata \(S_t\). Let \(\pi = P(\mathbf{ x}\in S_i)\) represent the size of \(S_i\). Obtain a random sample \(\mathbf{ x}_{ij}\), \(j = 1, \dots, n\) from \(S_i\). Then of course the \(n_i\) sum to \(n\). If \(I = 1\), we have random sampling over the entire sample space.

Latin hypercube sampling is an advanced form of stratified sampling. It ensures that each input variable’s distribution is fully represented by dividing the input space into \(M\) rows and columns, with samples taken such that each row and column contains only one sample. This method extends to multiple dimensions, providing a comprehensive sampling strategy.

The same reasoning that led to stratified sampling, ensuring that all portions of \(S\) were sampled, could lead further. If we wish to ensure also that each of the input variables \(\mathbf{ x}_k\) has all portions of its distribution represented by input values, we can divide the range of each \(\mathbf{ x}_k\) into \(n\) strata of equal marginal probability \(1/n\), and sample once from each stratum. Let this sample be \(\mathbf{ x}_{kj}\), \(j = 1, \dots, n\). These form the \(\mathbf{ x}_k\) component, \(k = 1, \dots , K\), in \(\mathbf{ x}_i\), \(i = 1, \dots, n\). The components of the various \(\mathbf{ x}_k\)’s are matched at random. This method of selecting input values is an extension of quota sampling (Steinberg 1963), and can be viewed as a \(K\)-dimensional extension of Latin square sampling (Raj 1968).

The paper’s rather dated reference to “Output from a Computer Code” highlights the historical context of these methods, which remain relevant today. Tony O’Hagan, who was a colleague in Sheffield when I first arrived there, was a pioneer in Gaussian process models, and has contributed significantly to this field, including work on managing uncertainty in computational models (Kennedy and O’Hagan, 2001). More information can be found in the technical reports from the EPSRC funded project http://www.mucm.ac.uk/.

Another key group is the “MASCOT-NUM Research Group” in France and it’s follow on RT-UQ, https://uq.math.cnrs.fr/, which unites statisticians, applied mathematicians, and engineers to tackle these complex problems.

Generative AI for Emulation

While Gaussian processes provide an excellent framework for emulation when we have relatively few simulation runs, modern generative AI approaches become powerful when we have extensive archives of previous simulations. Google DeepMind’s GraphCast system provides an excellent example of this approach in weather forecasting.

Traditional numerical weather prediction requires solving complex partial differential equations on supercomputers, taking hours to complete. GraphCast was trained on archived weather forecasts from the European Centre for Medium-Range Weather Forecasts (ECMWF) (Lam et al., 2023). This ECMWF dataset - containing millions of previous forecasts and their outcomes - allowed the model to learn the complex patterns and physics underlying weather systems.

Figure: YouTube video of results from the GraphCast algorithm.

As a result GraphCast can produce forecasts of similar accuracy to traditional numerical methods in seconds rather than hours. This is possible because:

1. The model has seen millions of examples of how weather patterns evolve
2. The underlying physics, while complex, has regularities that can be learned
3. The training data comes from a consistent, high-quality source of simulations

In many domains, we don’t have access to such a vast archive and must rely on more data-efficient approaches like Gaussian processes.

Emukit Playground

Emukit playground is a software toolkit for exploring the use of statistical emulation as a tool. It was built by Leah Hirst, during her software engineering internship at Amazon and supervised by Cliff McCollum.

Figure: Emukit playground is a tutorial for understanding the simulation/emulation relationship. https://amzn.github.io/emukit-playground/

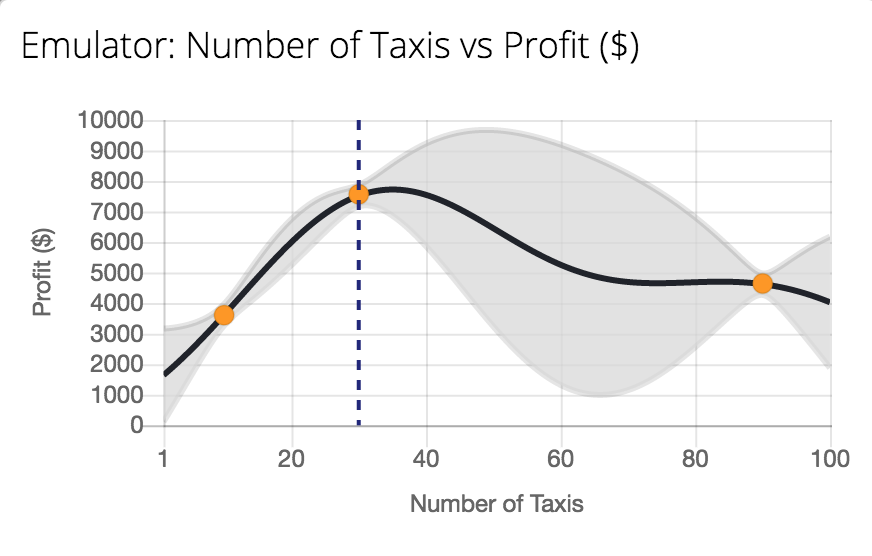
Figure: Tutorial on Bayesian optimization of the number of taxis deployed from Emukit playground. https://amzn.github.io/emukit-playground/#!/learn/bayesian_optimization

You can explore Bayesian optimization of a taxi simulation.

Exercise 3

You now know enough to build a simple emulation. To test your knowledge have a go at cobmining GPy with Thomas House’s herd immunity simulation. Can you build a Gaussian process emulator of the simulation? Don’t spent do long on this exercise. The idea is just to consolidate things like what the inputs and outputs should be.

Emukit

The Emukit software we will be using across the next part of this module is a python software library that facilitates emulation of systems. The software’s origins go back to work done by Javier Gonzalez as part of his post-doctoral project at the University of Sheffield. Javier led the design and build of a Bayesian optimization software. The package GPyOpt worked with the SheffieldML software GPy for performing Bayesian optimization.

GPyOpt had a modular design that allows the user to provide their own surrogate models, the package was built with GPy as a surrogate model in mind, but other surrogate models could also be wrapped and integrated.

However, GPyOpt didn’t allow the full flexibility of surrogate modelling for domains like experimental design, sensitivity analysis etc.

Emukit (Paleyes et al., 2019) is designed and built for a more general approach. The software is MIT licensed and its design and implementation was led by Javier Gonzalez and Andrei Paleyes at Amazon. Building on the experience of GPyOpt, the aim with Emukit was to use the modularisation ideas embedded in GPyOpt, but to extend them beyond the modularisation of the surrogate models to modularisation of the acquisition function.

Figure: The Emukit software is a set of software tools for emulation and surrogate modeling. https://emukit.github.io/emukit/

To use Emukit you need a set of models to use as the surrogates, we’ll use GPy.

Emukit does active experimental design, to access stratified sampling and latin hypercube designs it makes use of the pyDOE package.

%pip install pyDOE

The software was initially built by the team in Amazon. As well as Javier Gonzalez (ML side) and Andrei Paleyes (Software Engineering) the team included Mark Pullin, Maren Mahsereci, Alex Gessner, Aaron Klein, Henry Moss, David-Elias Künstle as well as management input from Cliff McCollum and myself.

Emukit Vision

Emulation in Emukit

We see emulation comprising of three main parts:

Models. This is a probabilistic data-driven representation of the process/simulator that the user is working with. There is normally a modelling framework that is used to create a model. Examples: neural network, Gaussian process, random forest.

Methods. Relatively low-level techniques that are aimed that either understanding, quantifying or using uncertainty that the model provides. Examples: Bayesian optimization, experimental design.

Tasks. High level goals that owners of the process/simulator might be interested in. Examples: measure quality of a simulator, explain complex system behavior.

Typical workflow that we envision for a user interested in emulation is:

1. Figure out which questions/tasks are important for them in regard to their process/simulation.

2. Understand which emulation techniques are needed to accomplish the chosen task.

3. Build an emulator of the process. That can be a very involved step, that may include a lot of fine tuning and validation.

Feed the emulator to the chosen technique and use it to answer the question/complete the task.

Emukit and Emulation

Figure: The emukit approach to the three parts of emulation.

Methods

This is the main focus of Emukit. Emukit defines a general structure of a decision-making method, called OuterLoop, and then offers implementations of few such methods: Bayesian optimization, experimental design. In addition to provide a framework for decision making Emukit provide other tools, like sensitivity analysis, that help to debug and interpret emulators. All methods in Emukit are model agnostic.

Models

Generally speaking, Emukit does not provide modelling capabilities, instead expecting users to bring their own models. Because of the variety of modelling frameworks out there, Emukit does not mandate or make any assumptions about a particular modelling technique or a library. Instead, it suggests to implement a subset of defined model interfaces required to use a particular method. Nevertheless, there are a few model-related functionalities in Emukit: - Example models, which give users something to play with to explore Emukit. - Model wrappers, which are designed to help adapting models in particular modelling frameworks to Emukit interfaces. - Multi-fidelity models, implemented based on GPy.

Tasks

Emukit does not contribute much to this part at the moment. However, the Emukit team are on lookout for typical use cases for Emukit, and if a reoccuring pattern emerges, it may become a part of the library.

while stopping condition is not met:
    optimize acquisition function
    evaluate user function
    update model with new observation

Emukit is built in a modular way so that each component in this loop can be swapped out. This means that scientists, applied mathematicians, machine learnings, statisticians can swap out the relevant part of their method and build on the underlying structure. You just need to pick out the part that requires implementation.

Loop

The emukit.core.loop.OuterLoop class is the abstract loop where the different components come together. There are more specific loops for Bayesian optimization and experimental design that construct some of the component parts for you.

Model

All Emukit loops need a probabilistic model of the underlying system. Emukit does not provide functionality to build models as there are already many good modelling frameworks available in python. Instead, we provide a way of interfacing third part modelling libraries with Emukit. We already provide a wrapper for using a model created with GPy. For instructions on how to include your own model please see this notebook.

Different models and modelling frameworks will provide different functionality. For instance, a Gaussian process will usually have derivatives of the predictions available but random forests will not. These different functionalities are represented by a set of interfaces which a model implements. The basic interface that all models must implement is IModel, which implements functionality to make predictions and update the model but a model may implement any number of other interfaces such as IDifferentiable which indicates a model has prediction derivatives available.

Candidate Point Calculator

This class decides which point to evaluate next. The simplest implementation, SequentialPointCalculator, collects one point at a time by finding where the acquisition is a maximum by applying the acquisition optimizer to the acquisition function. More complex implementations will enable batches of points to be collected so that the user function can be evaluated in parallel.

Acquisition

The acquisition is a heuristic quantification of how valuable collecting a future point might be. It is used by the candidate point calculator to decide which point(s) to collect next.

Acquisition Optimizer

The AcquisitionOptimizer optimizes the acquisition function to find the point at which the acquisition is a maximum. This will use the acquisition function gradients if they are available. If gradients of the acquisition function are not available, it will either estimate them numerically or use a gradient free optimizer.

User Function

This is the function that we are trying to reason about. It can be either evaluated by the user or it can be passed into the loop and evaluated by Emukit.

Model Updater

The ModelUpdater class updates the model with new training data after a new point is observed and optimizes any hyper-parameters of the model. It can decide whether hyper-parameters need updating based on some internal logic.

Stopping Condition

The StoppingCondition class chooses when we should stop collecting points. The most commonly used example is to stop when a set number of iterations have been reached.

You can see more of Emukit being put into practice in this case study on Machine Learning in the Multiverse by Sam Bell.

Emukit Tutorial

Set up the python imports that Emukit will use.

import numpy as np
import GPy

Now set up Emukit to run.

from emukit.experimental_design.experimental_design_loop import ExperimentalDesignLoop

Let’s check the help function for the experimental design loop. This is the outer loop that provides all the decision making parts of Emukit.

ExperimentalDesignLoop?

Now let’s load in the model wrapper for our probabilistic model. In this case, instead of using GPy, we’ll make use of a simple model wrapper Emukit provides for a basic form of Gaussian process.

from emukit.model_wrappers import SimpleGaussianProcessModel

Let’s have a quick look at how the included GP model works.

SimpleGaussianProcessModel?

Now let’s create the data.

x_min = -30.0
x_max = 30.0

x = np.random.uniform(x_min, x_max, (10, 1))
y = np.sin(x) + np.random.randn(10, 1) * 0.05

To learn about how to include your own model in Emukit, check this notebook which shows how to include a sklearn GP model.

emukit_model = SimpleGaussianProcessModel(x, y)

from emukit.core import ParameterSpace, ContinuousParameter
from emukit.core.loop import UserFunctionWrapper

p = ContinuousParameter('c', x_min, x_max)
space = ParameterSpace([p])

loop = ExperimentalDesignLoop(space, emukit_model)
loop.run_loop(np.sin, 30)

plot_min = -40.0
plot_max = 40.0

real_x = np.arange(plot_min, plot_max, 0.2)
real_y = np.sin(real_x)

Figure: Experimental design in Emukit using the ExperimentalDesignLoop: learning function \(\sin(x)\) with Emukit.

Computer the predictions from the Emukit model.

predicted_y = []
predicted_std = []
for x in real_x:
    y, var = emukit_model.predict(np.array([[x]]))
    std = np.sqrt(var)
    predicted_y.append(y)
    predicted_std.append(std)

predicted_y = np.array(predicted_y).flatten()
predicted_std = np.array(predicted_std).flatten()

Figure: The fit to the sine function after runnning the Emukit ExperimentalDesignLoop.

Exercise 4

Repeat the above experiment but using the Gaussian process model from sklearn. You can see step by step instructions on how to do this in this notebook.

Emukit Overview Summary

The aim is to provide a suite where different approaches to emulation are assimilated under one roof. The current version of Emukit includes multi-fidelity emulation for build surrogate models when data is obtained from multiple information sources that have different fidelity and/or cost; Bayesian optimisation for optimising physical experiments and tune parameters of machine learning algorithms or other computational simulations; experimental design and active learning: design the most informative experiments and perform active learning with machine learning models; sensitivity analysis: analyse the influence of inputs on the outputs of a given system; and Bayesian quadrature: efficiently compute the integrals of functions that are expensive to evaluate. But it’s easy to extend.

This introduction is based on An Introduction to Experimental Design with Emukit written by Andrei Paleyes and Maren Mahsereci.

Model Free Experimental Design

Design of Experiments in Python

%pip install pyDOE

The pyDOE software is a python software package for design of experiments in python. It helps with model free experimental designs.

Approaches include Factorial Designs, Response Surface Designs and Randomized Designs. The software is hosted on Github https://github.com/tisimst/pyDOE/

https://pythonhosted.org/pyDOE/

Figure: Design of Experiments for Python software. It provides various model free approaches to experimental design.

Experimental Design in Emukit

Forrester Function

Alex Forrester

We’re going to make use of the Forrester function in our example below, a function developed as a demonstrator by Alex Forrester. Alex is a design engineer who makes extensive use of surrogate modelling in Engineering design.

You can see Alex talking about the use of Gaussian process surrogates in this online video lecture.

Figure: A kinematic simulation of the human body doing breaststroke that Alex uses as part of his work in optimization of human motion during sports.

The Forrester function (Forrester et al., 2008) is commonly used as a demonstrator function in surrogate modelling. It has the form \[ f(x) = (6x-2)^2\sin(12 x-4). \]

import numpy as np

x = np.linspace(0, 1, 100)
f = (6*x-2)**2 * np.sin(12*x-4)

Figure: The Forrester function is commonly used as an exemplar function for surrogate modelling and emulation. It has the form \(f(x) = (6x-2)^2\sin(12 x-4)\)

We’re going to introduce the experimental design acquisition functions by looking at the Forrester function (Forrester et al., 2008)

import numpy as np

from emukit.test_functions import forrester_function
#from emukit.core.loop.user_function import UserFunctionWrapper
#from emukit.core import ContinuousParameter, ParameterSpace

target_function, space = forrester_function()

x_plot = np.linspace(space.parameters[0].min, space.parameters[0].max, 301)[:, None]
y_plot = target_function(x_plot)

Figure: The Forrester function (Forrester et al., 2008).

Initial Design

Usually, before we start the actual ExpDesign loop we need to gather a few observations such that we can fit the model. This is called the initial design and common strategies are either a predefined grid or sampling points uniformly at random. These strategies are known as model-free experimental design.

X_init = np.array([[0.2],[0.6], [0.9]])
Y_init = target_function(X_init)

Figure: The initial design for the Forrester function example.

The Model

Now we can start with the ExpDesign loop by first fitting a model on the collected data. A popular model for ExpDesign is a Gaussian process (GP) which defines a probability distribution across classes of functions, typically smooth, such that each linear finite-dimensional restriction is multivariate Gaussian (Rasmussen and Williams, 2006). Gaussian processes are fully parametrized by a mean \(\mu(\mathbf{ x})\) and a covariance function \(k(\mathbf{ x},\mathbf{ x}^\prime)\). Without loss of generality \(\mu(\mathbf{ x})\) is assumed to be zero. The covariance function \(k(\mathbf{ x},\mathbf{ x}^\prime)\) characterizes the smoothness and other properties of \(f\). It is known that the kernel of the process has to be continuous, symmetric and positive definite. A widely used kernel is the exponentiated quadratic or RBF kernel: \[ k(\mathbf{ x},\mathbf{ x}^\prime) = \alpha \exp{ \left(-\frac{\|\mathbf{ x}-\mathbf{ x}^\prime\|^2}{2 \ell}\right)} \] where \(\alpha\) and \(\ell\) are hyperparameters.

To denote that \(f\) is a sample from a GP with mean \(\mu\) and covariance \(k\) we write \[ f\sim \mathcal{GP}(\mu,k). \]

For regression tasks, the most important feature of GPs is that process priors are conjugate to the likelihood from finitely many observations \(\mathbf{Y}= (y_1,\dots,y_n)^\top\) and \(\mathbf{X}=\{\mathbf{ x}_1,\dots,\mathbf{ x}_n\}\), \(\mathbf{ x}_i\in \mathcal{X}\) of the form \(y_i = f(\mathbf{ x}_i) + \epsilon_i\) where \(\epsilon_i \sim \mathcal{N}\left(0,\sigma^2\right)\) and we typically estimate \(\sigma^2\) by maximum likelihood alongside \(\alpha\) and \(\ell\).

We obtain the Gaussian posterior \[ f(\mathbf{ x}^*)|\mathbf{X}, \mathbf{Y}, \theta \sim \mathcal{N}\left(\mu(\mathbf{ x}^*),\sigma^2(\mathbf{ x}^*)\right), \] where \(\mu(\mathbf{ x}^*)\) and \(\sigma^2(\mathbf{ x}^*)\) have a closed form solution as we’ve seen in the earlier lectures (see also Rasmussen and Williams (2006)).

Note that Gaussian processes are also characterized by hyperparameters, for example in the exponentiated quadratic case we have \(\boldsymbol{ \theta}= \left\{ \alpha, \ell, \sigma^2 \right\}\) for the scale of the covariance, the lengthscale and the noise variance. Here, for simplicity we will keep these hyperparameters fixed. However, we will usually either optimize or sample these hyperparameters using the marginal loglikelihood of the GP.

In this module we’ve focussed on Gaussian processes, but we could also use any other model that returns a mean \(\mu(\mathbf{ x})\) and variance \(\sigma^2(\mathbf{ x})\) on arbitrary input points \(\mathbf{ x}\) such as Bayesian neural networks or random forests. In Emukit these different models can also be used by defining a new ModelWrapper.

Here we’re going to wrap a GPy model.

import GPy
from emukit.model_wrappers.gpy_model_wrappers import GPyModelWrapper

Now we set up the covariance function for the GPy model, initialising it with a lengthscale, \(\ell=0.08\), and a variance, \(\alpha=20\).

kern = GPy.kern.RBF(1, lengthscale=0.08, variance=20)
gpy_model = GPy.models.GPRegression(X_init, Y_init, kern, noise_var=1e-10)
emukit_model = GPyModelWrapper(gpy_model)

mu_plot, var_plot = emukit_model.predict(x_plot)

Figure: The emulator fitted to the Forrester function with only three observations from the inital design. The error bars show 1, 2 and 3 standard deviations.

The Acquisition Function

In the second step of our ExpDesign loop we use our model to compute the acquisition function. We’ll review two different forms of acquisition funciton for doing this.

Uncertainty Sampling

In uncertainty sampling (US) we hoose the next value \(\mathbf{ x}_{n+1}\) at the location where the model on \(f(\mathbf{ x})\) has the highest marginal predictive variance \[ a_{US}(\mathbf{ x}) = \sigma^2(\mathbf{ x}). \] This makes sure, that we learn the function \(f(\cdot)\) everywhere on \(\mathbb{X}\) to a similar level of absolute error.

Integrated Variance Reduction

In the integrated variance reduction (IVR) you choose the next value \(\mathbf{ x}_{n+1}\) such that the total variance of the model is reduced maximally (Sacks et al., 1989), \[ \begin{align*} a_{\text{IVR}} & = \int_{\mathbb{X}}[\sigma^2(\mathbf{ x}') - \sigma^2(\mathbf{ x}'; \mathbf{ x})]\text{d}\mathbf{ x}' \\ & \approx \frac{1}{\# \text{samples}}\sum_i^{\# \text{samples}}[\sigma^2(\mathbf{ x}_i) - \sigma^2(\mathbf{ x}_i; \mathbf{ x})]. \end{align*} \] Here \(\sigma^2(\mathbf{ x}'; \mathbf{ x})\) is the predictive variance at \(\mathbf{ x}'\) had \(\mathbf{ x}\) been observed. Thus IVR computes the overall reduction in variance (for all points in \(\mathbb{X}\)) had \(f\) been observed at \(\mathbf{ x}\).

The finite sum approximation on the right-hand side of the equation is usually used because the integral over \(\mathbf{ x}'\) is not analytic. In that case \(\mathbf{ x}_i\) are sampled randomly. For a GP model the right-hand side simplifies to

\[ a_{LCB} \approx \frac{1}{\# \text{samples}}\sum_i^{\# \text{samples}}\frac{k^2(\mathbf{ x}_i, \mathbf{ x})}{\sigma^2(\mathbf{ x})}. \]

IVR is arguably the more principled approach, but often US is preferred over IVR simply because it lends itself to gradient based optimization more easily, is cheaper to compute, and is exact.

For both of them (stochastic) gradient base optimizers are used to retrieve \(\mathbf{ x}_{n+1} \in \operatorname*{arg\:max}_{\mathbf{ x}\in \mathbb{X}} a(\mathbf{ x})\).

from emukit.experimental_design.acquisitions import IntegratedVarianceReduction, ModelVariance

us_acquisition = ModelVariance(emukit_model)
ivr_acquisition = IntegratedVarianceReduction(emukit_model, space)

us_plot = us_acquisition.evaluate(x_plot)
ivr_plot = ivr_acquisition.evaluate(x_plot)

Figure: The uncertainty sampling and integrated variance reduction acquisition functions for the Forrester example.

Evaluating the objective function

To find the next point to evaluate we optimize the acquisition function using a standard gradient descent optimizer.

from emukit.core.optimization import GradientAcquisitionOptimizer

optimizer = GradientAcquisitionOptimizer(space)
x_new, _ = optimizer.optimize(us_acquisition)

Figure: The maxima of the acquisition function is found and this point is selected for inclusion.

Afterwards we evaluate the true objective function and append it to our initial observations.

y_new = target_function(x_new)

X = np.append(X_init, x_new, axis=0)
Y = np.append(Y_init, y_new, axis=0)

After updating the model, you can see that the uncertainty about the true objective function in this region decreases and our model becomes more certain.

emukit_model.set_data(X, Y)
mu_plot, var_plot = emukit_model.predict(x_plot)

Figure: The target Forrester function plotted alongside the emulation model and error bars from the emulation at 1, 2 and 3 standard deviations.

We can repeat this process to obtain more points.

us_acquisition = ModelVariance(emukit_model)
us_plot = us_acquisition.evaluate(x_plot)
x_new, _ = optimizer.optimize(us_acquisition)

Figure: The maxima of the acquisition function is found and this point is selected for inclusion.

Once again we can asimmilate the new target function observation into the model and re-evaluate our emulation.

y_new = target_function(x_new)
X = np.append(X, x_new, axis=0)
Y = np.append(Y, y_new, axis=0)
emukit_model.set_data(X, Y)
mu_plot, var_plot = emukit_model.predict(x_plot)

Resulting in an updated estimate of the function.

Figure: The target Forrester function plotted alongside the emulation model and error bars from the emulation at 1, 2 and 3 standard deviations.

Emukit’s Experimental Design Interface

Of course in practice we don’t want to implement all of these steps our self. Emukit provides a convenient and flexible interface to apply experimental design. Below we can see how to run experimental design on the exact same function for 10 iterations.

from emukit.experimental_design.experimental_design_loop import ExperimentalDesignLoop

ed = ExperimentalDesignLoop(space=space, model=emukit_model)

ed.run_loop(target_function, 10)

mu_plot, var_plot = ed.model.predict(x_plot)

Figure: The fit of the model to the Forrester function.

Conclusions

We’ve introduced the Emukit software and outlined its design philosophy. We’ve then performed some simple examples using Emukit to perform experimental design as a task. In particular we saw how we could define the task as an acquisition funciton, a loop, an emulator model and a target function.

You can compare the design of this software with its predecessor, GPyOpt, which is less modular in its design, and more focussed on Bayesian optimization.

Thanks!

For more information on these subjects and more you might want to check the following resources.

• book: The Atomic Human
• twitter: @lawrennd
• podcast: The Talking Machines
• newspaper: Guardian Profile Page
• blog: http://inverseprobability.com

References