Week 3: Emulation

[jupyter][google colab][reveal]

Neil D. Lawrence

Abstract:

In this lecture we motivate the use of emulation and introduce the GPy software as a framework for building Gaussian process emulators.

notutils

This small package is a helper package for various notebook utilities used below.

The software can be installed using

%pip install notutils

from the command prompt where you can access your python installation.

The code is also available on GitHub: https://github.com/lawrennd/notutils

Once notutils is installed, it can be imported in the usual manner.

import notutils

mlai

The mlai software is a suite of helper functions for teaching and demonstrating machine learning algorithms. It was first used in the Machine Learning and Adaptive Intelligence course in Sheffield in 2013.

The software can be installed using

%pip install mlai

from the command prompt where you can access your python installation.

The code is also available on GitHub: https://github.com/lawrennd/mlai

Once mlai is installed, it can be imported in the usual manner.

import mlai
from mlai import plot

Accelerate Programme

The Computer Lab is hosting a new initiative, funded by Schmidt Futures, known as the Accelerate Programme for Scientific Discovery. The aim is to address scientific challenges, and accelerate the progress of research, through using tools in machine learning.

We now have four fellows appointed, each of whom works at the interface of machine learning and scientific discovery. They are using the ideas around machine learning modelling to drive their scientific research.

For example, Bingqing Cheng, one of the Department’s former DECAF Fellows has used neural network accelerated molecular dynamics simulations to understand a new form of metallic hydrogen, likely to occur at the heart of stars (Cheng et al., 2020). The University’s press release is here.

Related Approaches

While this module is mainly focusing on emulation as a route to bringing machine learning closer to the physical world, I don’t want to give the impression that’s the only approach. It’s worth bearing in mind three important domains of machine learning (and statistics) that we also could have explored.

• Probabilistic Programming
• Approximate Bayesian Computation
• Causal inference

Each of these domains also brings a lot to the table in terms of understanding the physical world.

Probabilistic Programming

Probabilistic programming is an idea that, from our perspective, can be summarized as follows. What if, when constructing your simulator, or your model, you used a programming language that was aware of the state variables and the probability distributions. What if this language could ‘compile’ the program into code that would automatically compute the Bayesian posterior for you?

This is the objective of probabilistic programming. The idea is that you write your model in a language, and that language is automatically converted into the different modelling codes you need to perform Bayesian inference.

The ideas for probabilistic programming originate in BUGS. The software was developed at the MRC Biostatistics Unit here in Cambridge in the early 1990s, by among others, Sir David Spiegelhalter. Carl Henrik covered in last week’s lecture some of the approaches for approximate inference. BUGS uses Gibbs sampling. Gibbs sampling, however, can be slow to converge when there are strong correlations in the posterior between variables.

Approximate Bayesian Computation

We reintroduced Gaussian processes at the start of this lecture by sampling from the Gaussian process and matching the samples to data, discarding those that were distant from our observations. This approach to Bayesian inference is the starting point for approximate Bayesian computation or ABC.

The idea is straightforward, if we can measure ‘closeness’ in some relevant fashion, then we can sample from our simulation, compare our samples to real world data through ‘closeness measure’ and eliminate samples that are distant from our data. Through appropriate choice of closeness measure, our samples can be viewed as coming from an approximate posterior.

My Sheffield colleague, Rich Wilkinson, was one of the pioneers of this approach during his PhD in the Statslab here in Cambridge. You can hear Rich talking about ABC at NeurIPS in 2013 here.

Figure: Rich Wilkinson giving a Tutorial on ABC at NeurIPS in 2013. Unfortunately, they’ve not synchronised the slides with the tutorial. You can find the slides separately here.

Causality

Figure: Judea Pearl and Elias Bareinboim giving a Tutorial on Causality at NeurIPS in 2013. Again, the slides aren’t synchronised, but you can find them separately here.

All these approaches offer a lot of promise for developing machine learning at the interface with science but covering each in detail would require four separate modules. We’ve chosen to focus on the emulation approach, for two principal reasons. Firstly, it’s conceptual simplicity. Our aim is to replace all or part of our simulation with a machine learning model. Typically, we’re going to want uncertainties as part of that representation. That explains our focus on Gaussian process models. Secondly, the emulator method is flexible. Probabilistic programming requires that the simulator has been built in a particular way, otherwise we can’t compile the program. Finally, the emulation approach can be combined with any of the existing simulation approaches. For example, we might want to write our emulators as probabilistic programs. Or we might do causal analysis on our emulators, or we could speed up the simulation in ABC through emulation.

We’ve introduced the notion of a simulator. A body of computer code that expresses our understanding of a particular physical system. We introduced such simulators through physical laws, such as laws of gravitation or electro-magnetism. But we soon saw that in many simulations those laws become abstracted, and the simulation becomes more phenomological.

Even full knowledge of all laws does not give us access to ‘the mind of God’, because we are lacking information about the data, and we are missing the compute. These challenges further motivate the need for abstraction, and we’ve seen examples of where such abstractions are used in practice.

The example of Conway’s Game of Life highlights how complex emergent phenomena can require significant computation to explore.

Emulation

There are a number of ways we can use machine learning to accelerate scientific discovery. But one way is to have the machine learning model learn the effect of the rules. Rather than worrying about the detail of the rules through computing each step, we can have the machine learning model look to abstract the rules and capture emergent phenomena, just as the Maxwell-Boltzmann distribution captures the essence of the behavior of the ideal gas.

The challenges of Laplace’s gremlin present us with issues that we solve in a particular way, this is the focus of Chapter 6 in The Atomic Human.

The Atomic Human

Figure: The Atomic Human (Lawrence, 2024).

What follows is a quote form Chapter 6, which introduces Laplace’s gremlin and its consequences.

Deep Thought and the Challenge of Computation

In Douglas Adams’s Hitchhiker’s Guide to the Galaxy the computer Deep Thought is asked to provide the answer to the ‘great question’ of ‘life, the universe and everything’. After seven and a half million years of computation, Deep Thought has completed its program but is reluctant to give its creators the answer.

‘You’re really not going to like it,’ observed Deep Thought.
‘Tell us!’
‘All right,’ said Deep Thought. ‘The Answer to the Great Question . . .’
‘Yes . . . !’
‘Of Life, the Universe and Everything …’ said Deep Thought.
‘Yes … !’
‘Is …’ said Deep Thought, and paused.
‘Yes … !’
‘Is …’
‘Yes … !!! … ?’
‘Forty-two,’ said Deep Thought, with infinite majesty and calm.

Douglas Adams The Hitchhiker’s Guide to the Galaxy, 1979, Chapter 27

After a period of shock from the questioners, the machine goes on to explain:

‘I checked it very thoroughly,’ said the computer, ‘and that quite definitely is the answer. I think the problem, to be quite honest with you, is that you’ve never actually known what the question is.’

Douglas Adams The Hitchhiker’s Guide to the Galaxy, 1979, Chapter 28

To understand the question, Deep Thought goes on to agree to design a computer which will work out what the question is. In the book that machine is the planet Earth, and its operators are mice. Deep Thought’s idea is that the mice will observe the Earth and their observations will allow them to know what the Great Question is.

To understand the consequences of Hawking’s Theory of Everything, we would have to carry out a scheme similar to Deep Thought’s. The Theory wouldn’t directly tell us that hurricanes exist or that when the sun sets on Earth the sky will have a red hue. It wouldn’t directly tell us that water will boil at 100 degrees centigrade. These consequences of the Theory would only play out once it was combined with the data to give us the emergent qualities of the Universe. The Deep Thought problem hints at the intractability of doing this. The computation required to make predictions from Laplace’s demon can be enormous, Deep Thought intends to create a planet to run it. As a result, this isn’t how our intelligence works in practice. The computations required are just too gargantuan. Relative to the scale of the Universe our brains are extremely limited. Fortunately though, to make these predictions, we don’t have to build our own Universe, because we’ve already got one.

Figure: Rabbit and Pooh watch the result of Pooh’s hooshing idea to move Eeyore towards the shore.

When you are a Bear of Very Little Brain, and you Think of Things, you find sometimes that a Thing which seemed very Thingish inside you is quite different when it gets out into the open and has other people looking at it.

A.A. Milne as Winnie-the-Pooh in The House at Pooh Corner, 1928

This comment from Pooh bear comes just as he’s tried to rescue his donkey friend, Eeyore, from a river by dropping a large stone on him from a bridge. Pooh’s idea had been to create a wave to push the donkey to the shore, a process that Pooh’s rabbit friend calls “hooshing”.

Hooshing is a technique many children will have tried to retrieve a ball from a river. It can work, so Pooh’s idea wasn’t a bad one, but the challenge he faced was in its execution. Pooh aimed to the side of Eeyore, unfortunately the stone fell directly on the stuffed donkey. But where is Laplace’s demon in hooshing? Just as we can talk about Gliders and Loafers in Conway’s Game of Life, we talk about stones and donkeys in our Universe. Pooh’s prediction that he can hoosh the donkey with the stone is not based on the Theory, it comes from observing the way objects interact in the actual Universe. Pooh is like the mice in Douglas Adams’s Earth. He is observing his environment. He looks for patterns in that environment. Pooh then borrows the computation that the Universe has already done for us. He has seen similar situations before, perhaps he once used a stone to hoosh a ball. He is then generalising from these previous circumstances to suggest that he can also hoosh the donkey. Despite being a bear of little brain, like the mice on Adams’s Earth, Pooh can answer questions about his universe by observing the results of the Theory of Everything playing out around him.

Surrogate Modelling in Practice

The knowledge of ones own limitations that Pooh shows is sometimes known as Socratic wisdom, and its a vital part of our intelligence. It expresses itself as humility and skepticism.

In the papers we reviewed last lecture, neural networks are being used to speed up computations. In this course we’ve introduced Gaussian processes that will be used to speed up these computations. In both cases the ideas are similar. Rather than rerunning the simulation, we use data from the simulation to fit the neural network or the Gaussian process to the data.

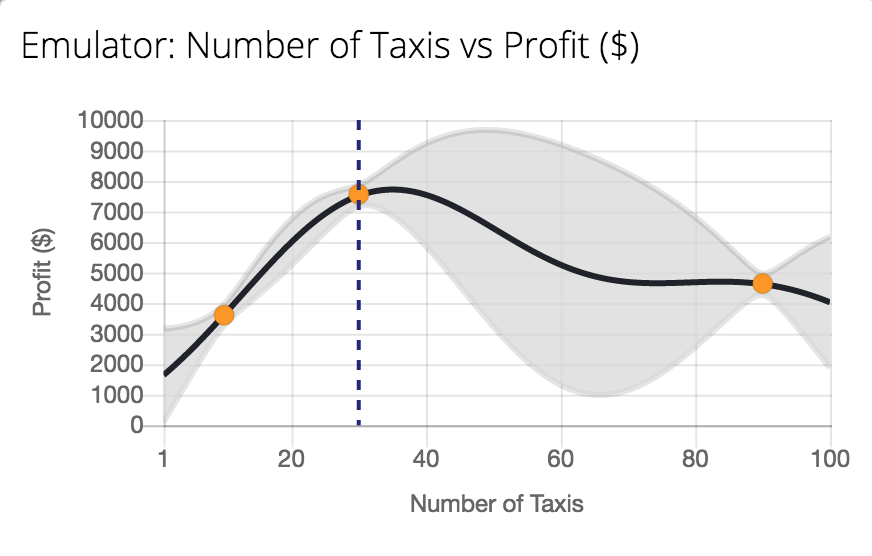
We’ll see an example of how this is done in a moment, taken from a simple ride hailing simulator, but before we look at that, we’ll first consider why this might be a useful approach.

As we’ve seen from the very simple rules in the Game of Life, emergent phenomena we might be interested in take computation power to discover, just as Laplace’s and Dirac’s quotes suggest. The objective in surrogate modelling is to harness machine learning models to learn those physical characteristics.

Types of Simulations

Differential Equation Models

Differential equation models form the backbone of many scientific simulations. These can be either abstracted, like epidemiological models that treat populations as continuous quantities, or fine-grained like climate models that solve complex systems of equations. These models are based on mathematical representations of physical laws or system behavior and often require sophisticated numerical methods for their solution.

Discrete Event Simulations

Discrete event simulations come in two main varieties. Turn-based simulations, like Conway’s Game of Life or Formula 1 strategy simulations, update their state at regular intervals. Event-driven simulations, like the Gillespie algorithm used in chemical models, advance time to the next event, which might occur at irregular intervals. Both approaches are particularly useful when studying systems that change state at distinct moments rather than continuously.

Software System Simulations

A third important category is software system simulation, particularly relevant in modern computing environments. These simulations allow testing of production code systems, enabling “what if” scenarios and counterfactual analysis. They might involve rerunning entire codebases with simulated inputs, which is particularly valuable when dealing with complex systems with multiple interacting components.

F1 and Fidelity

Formula 1 race simulations contain assumptions that derive from physics but don’t directly encode the physical laws. For example, if one car is stuck behind another, in any given lap, it might overtake. A typical race simulation will look at the lap speed of each car and the top speed of each car (as measured in ‘speed traps’ that are placed on the straight). It will assume a probability of overtake for each lap that is a function of these values. Of course, underlying that function is the physics of how cars overtake each other, but that can be abstracted away into a simpler function that the Race Strategy Engineer defines from their knowledge and previous experience.

Many simulations have this characteristic: major parts of the simulation are the result of encoding expert knowledge in the code. But this can lead to challenges. I once asked a strategy engineer, who had completed a new simulation, how it was going. He replied that things had started out well, but over time its performance was degrading. We discussed this for a while and over time a challenge of mis-specified granularity emerged.

The engineer explained how there’d been a race where the simulation had suggested that their main driver shouldn’t pit because he would have emerged behind a car with a slower lap speed, but a high top-speed. This would have made that car difficult to overtake. However, the driver of that slower car was also in the team’s ‘development program’, so everyone in the team knew that the slower car would have moved aside to let their driver through. Unfortunately, the simulation didn’t know this. So, the team felt the wrong stategy decision was made. After the race, the simulation was updated to include a special case for this situation. The new code checked whether the slower car was a development driver, making it ‘more realistic’.

Over time there were a number of similar changes, each of which should have improved the simulation, but the reality was the code was now ‘mixing granularities’. The formula for computing the probability of overtake as a function of speeds is one that is relatively easy to verify. It ignores the relationships between drivers, whether a given driver is a development driver, whether one bears a grudge or not, whether one is fighting for their place in the team. That’s all assimilated into the equation. The original equation is easy to calibrate, but as soon as you move to a finer granularity and consider more details about individual drivers, the model seems more realistic, but it becomes difficult to specify, and therefore performance degrades.

Simulations work at different fidelities, but as the Formula 1 example shows you must be very careful about mixing fidelities within the same simulation. The appropriate fidelity of a simulation is strongly dependent on the question being asked of it. On the context. For example, in Formula 1 races you can also simulate the performance of the car in the wind tunnel and using computational fluid dynamics representations of the Navier-Stokes equations. That level of fidelity is appropriate when designing the aerodynamic components of the car, but inappropriate when building a strategy simulation.

The original overtaking probability calculations were clean and verifiable. But by mixing in team politics and driver relationships, they created a model that was harder to specify correctly.

The same team also uses highly detailed aerodynamics simulations with computational fluid dynamics for car design. This different fidelity is appropriate there - but mixing fidelities within a single simulation often causes more problems than it solves. The key is maintaining consistent granularity appropriate to the specific question being asked.

Epidemiology

The same concept of modelling at a particular fidelity comes up in epidemiology. Disease is transmitted by direct person to person interactions between individuals and objects. But in theoretical epidemiology, this is approximated by differential equations. The resulting models look very similar to reaction rate models used in Chemistry for well mixed beakers. Let’s have a look at a simple example used for modelling the policy of ‘herd immunity’ for Covid19.

Modelling Herd Immunity

This example is taken from Thomas House’s blog post on Herd Immunity. This model was shared at the beginning of the Covid19 pandemic when the first UK lockdown hadn’t yet occurred.

import numpy as np
from scipy import integrate

The next piece of code sets up the dynamics of the compartmental model. He doesn’t give the specific details in the blog post, but my understanding is that the four states are as follows. x[0] is the susceptible population, those that haven’t had the disease yet. The susceptible population decreases by encounters with infections people. In Thomas’s model, both x[3] and x[4] are infections. So, the dynamics of the reduction of the susceptible is given by \[ \frac{\text{d}{S}}{\text{d}t} = - \beta S (I_1 + I_2). \] Here, we’ve used \(I_1\) and \(I_2\) to represent what appears to be two separate infectious compartments in Thomas’s model. We’ll speculate about why there are two in a moment.

The model appears to be an SEIR model, so rather than becoming infectious directly you next move to an ‘exposed’, where you have the disease, but you are not yet infectious. There are again two exposed states, we’ll return to that in a moment. We denote the first, x[1] by \(E_1\). We have \[ \frac{\text{d}{E_1}}{\text{d}t} = \beta S (I_1 + I_2) - \sigma E_1. \] Note that the first term matches the term from the Susceptible equation. This is because it is the incoming exposed population.

The exposed population move to a second compartment of exposure, \(E_2\). I believe the reason for this is that if you use only one exposure compartment, then the statistics of the duration of exposure are incorrect (implicitly they are exponentially distributed in the underlying stochastic version of the model). By using two exposure departments, Thomas is making a slight correction to this which would impose a first order gamma distribution on those statistics. A similar trick is being deployed for the ‘infectious group’. So, we gain an additional equation to help with these statistics, \[ \frac{\text{d}{E_2}}{\text{d}t} = \sigma E_1 - \sigma E_2. \] giving us the exposed group as the sum of the two compartments \(E_1\) and \(E_2\). The exposed group from the second compartment then become ‘infected’, which we represent with \(I_1\), in the code this is x[3], \[ \frac{\text{d}{I_1}}{\text{d}t} = \sigma E_2 - \gamma I_1, \] and similarly, Thomas is using a two-compartment infectious group to fix up the duration model. So we have, \[ \frac{\text{d}{I_2}}{\text{d}t} = \gamma I_1 - \gamma I_2. \] And finally, we have those that have recovered emerging from the second infections compartment. In this model there is no separate model for ‘deaths’, so the recovered compartment, \(R\), would also include those that die, \[ \frac{\text{d}R}{\text{d}t} = \gamma I_2. \] All these equations are then represented in code as follows.

def odefun(t,x,beta0,betat,t0,t1,sigma,gamma):
    dx = np.zeros(6)
    if ((t>=t0) and (t<=t1)):
        beta = betat
    else:
        beta = beta0
    dx[0] = -beta*x[0]*(x[3] + x[4])
    dx[1] = beta*x[0]*(x[3] + x[4]) - sigma*x[1]
    dx[2] = sigma*x[1] - sigma*x[2]
    dx[3] = sigma*x[2] - gamma*x[3]
    dx[4] = gamma*x[3] - gamma*x[4]
    dx[5] = gamma*x[4]
    return dx

Where the code takes in the states of the compartments (the values of x) and returns the gradients of those states for the provided parameters (sigma, gamma and beta). Those parameters are set according to the known characteristics of the disease.

The next block of code sets up the parameters of the SEIR model. A particularly important parameter is the reproduction number (\(R_0\)), here Thomas has assumed a reproduction number of 2.5, implying that each infected member of the population transmits the infection up to 2.5 other people. The effective \(R\) decreases over time though, because some of those people they meet will no longer be in the susceptible group.

# Parameters of the model
N = 6.7e7 # Total population
i0 = 1e-4 # 0.5*Proportion of the population infected on day 0
tlast = 365.0 # Consider a year
latent_period = 5.0 # Days between being infected and becoming infectious
infectious_period = 7.0 # Days infectious
R0 = 2.5 # Basic reproduction number in the absence of interventions
Rt = 0.75 # Reproduction number in the presence of interventions
tend = 21.0 # Number of days of interventions

The parameters are correct for the ‘discrete system’, where the infectious period is a discrete time, and the numbers are discrete values. To translate into our continuous differential equation system’s parameters, we need to do a couple of manipulations. Note the factor of 2 associated with gamma and sigma. This is a doubling of the rate to account for the fact that there are two compartments for each of these states (to fix-up the statistics of the duration models).

beta0 = R0 / infectious_period
betat = Rt / infectious_period
sigma = 2.0 / latent_period
gamma = 2.0 / infectious_period

Next, we solve the system using scipy’s initial value problem solver. The solution method is Runge-Kutta-Fehlberg method, as indicated by the 'RK45' solver. This is a numerical method for solving differential equations. The 45 is the order of the method and the error estimator.

We can view the solver itself as somehow a piece of simulation code, but here it’s being called as sub routine in the system. It returns a solution for each time step, stored in a list sol.

This is typical of this type of non-linear differential equation problem. Whether it’s partial differential equations, ordinary differential equations, there’s a step where a numerical solver needs to be called. These are often expensive to run. For climate and weather models, this would be where we solved the Navier-Stokes equations. For this simple model, the solution is relatively quick.

t0ran = np.array([-100, 40, 52.5, 65])
sol=[]
for tt in range(0,len(t0ran)):
    sol.append(integrate.solve_ivp(lambda t,x: odefun(t,x,beta0,betat,t0ran[tt],t0ran[tt]+tend,sigma,gamma),
                              (0.0,tlast),
                              np.array([1.0-2.0*i0, 0.0, 0.0, i0, i0, 0.0]),
                              'RK45',
                              atol=1e-8,
                              rtol=1e-9))

Figure: A zoomed in version of Thomas House’s variation on the SEIR model for evaluating the effect of early interventions.

Figure: The full progress of the disease in Thomas House’s variation on the SEIR model for evaluating the effect of early interventions.

In practice, immunity for Covid19 may only last around 6 months. As an exercise, try to extend Thomas’s model for the case where immunity is temporary. You’ll need to account for deaths as well in your new model.

Thinking about our Formula 1 example, and the differing levels of fidelity that might be included in a model, you can now imagine the challenges of doing large scale theoretical epidemiology. The compartment model is operating at a particular level of fidelity. Imagine trying to modify this model for a specific circumstance, like the way that the University of Cambridge chooses to do lectures. It’s not appropriate for this level of fidelity. You need to use different types of models for that decision making. One of our case studies looks at a simulation that was used to advise the government on the Test Trace Isolate program that took a different approach (The DELVE Initiative, 2020).

Strategies for Simulation

Within any simulation, we can roughly split the variables of interest into the state variables and the parameters. In the Herd immunity example, the state variables were the different susceptible, exposed, infectious and recovered groups. The parameters were the reproduction number and the expected lengths of infection and the timing of lockdown. Often parameters are viewed as the inputs to the simulation, the things we can control. We might want to know how to time lock down to minimize the number of deaths. This behavior of the simulator is what we may want to emulate with our Gaussian process model.

So far, we’ve introduced simulation motivated by the physical laws of the universe. Those laws are sometimes encoded in differential equations, in which case we can try to solve those systems (like with Herd Immunity or Navier Stokes). An alternative approach is taken in the Game of Life. There a turn-based simulation is used, at each turn, we iterate through the simulation updating the state of the simulation. This is known as a discrete event simulation. In race simulation for Formula 1 a discrete event simulation is also used. There is another form of discrete event simulation, often used in chemical models, where the events don’t take place at regular intervals. Instead, the timing to the next event is computed, and the simulator advances that amount of time. For an example of this see the Gillespie algorithm.

There is a third type of simulation that we’d also like to introduce. That is simulation within computer software. In particular, the need to backtest software with ‘what if’ ideas – known as counter factual simulation – or to trace errors that may have occurred in production. This can involve loading up entire code bases and rerunning them with simulated inputs. This is a third form of simulation where emulation can also come in useful.

Backtesting Production Code

In large-scale production systems, simulation takes on a different character. Rather than modeling physical phenomena, we need to simulate entire software systems. At Amazon, for example, we worked with simulations ranging from Prime Air drones to supply chain systems. In a purchasing system, the idea is to store stock to balance supply and demand. The aim is to keep product in stock for quick dispatch while keeping prices (and therefore costs) low. This idea is at the heart of Amazon’s focus on customer experience.

Alexa

Figure: Alexa Architecture overview taken from the Alexa Skills programme.

Figure: Rohit Prasad talking about Alexa at the Amazon 2019 re:MARS event.

Figure: Simple schmeatic of an intelligent agent’s components.

Speech to Text

Cloud Service: Knowledge Base

Text to Speech

Prime Air

One project where the components of machine learning and the physical world come together is Amazon’s Prime Air drone delivery system.

Automating the process of moving physical goods through autonomous vehicles completes the loop between the ‘bits’ and the ‘atoms’. In other words, the information and the ‘stuff’. The idea of the drone is to complete a component of package delivery, the notion of last mile movement of goods, but in a fully autonomous way.

Figure: An actual ‘Santa’s sleigh’. Amazon’s prototype delivery drone. Machine learning algorithms are used across various systems including sensing (computer vision for detection of wires, people, dogs etc) and piloting. The technology is necessarily a combination of old and new ideas. The transition from vertical to horizontal flight is vital for efficiency and uses sophisticated machine learning to achieve.

As Jeff Wilke (who was CEO of Amazon Retail at the time) announced in June 2019 the technology is ready, but still needs operationalization including e.g. regulatory approval.

Figure: Jeff Wilke (CEO Amazon Consumer) announcing the new drone at the Amazon 2019 re:MARS event alongside the scale of the Amazon supply chain.

When we announced earlier this year that we were evolving our Prime two-day shipping offer in the U.S. to a one-day program, the response was terrific. But we know customers are always looking for something better, more convenient, and there may be times when one-day delivery may not be the right choice. Can we deliver packages to customers even faster? We think the answer is yes, and one way we’re pursuing that goal is by pioneering autonomous drone technology.

Today at Amazon’s re:MARS Conference (Machine Learning, Automation, Robotics and Space) in Las Vegas, we unveiled our latest Prime Air drone design. We’ve been hard at work building fully electric drones that can fly up to 15 miles and deliver packages under five pounds to customers in less than 30 minutes. And, with the help of our world-class fulfillment and delivery network, we expect to scale Prime Air both quickly and efficiently, delivering packages via drone to customers within months.

The 15 miles in less than 30 minutes implies air speed velocities of around 50 kilometers per hour.

Our newest drone design includes advances in efficiency, stability and, most importantly, in safety. It is also unique, and it advances the state of the art. How so? First, it’s a hybrid design. It can do vertical takeoffs and landings – like a helicopter. And it’s efficient and aerodynamic—like an airplane. It also easily transitions between these two modes—from vertical-mode to airplane mode, and back to vertical mode.

It’s fully shrouded for safety. The shrouds are also the wings, which makes it efficient in flight.

Figure: Picture of the drone from Amazon Re-MARS event in 2019.

Our drones need to be able to identify static and moving objects coming from any direction. We employ diverse sensors and advanced algorithms, such as multi-view stereo vision, to detect static objects like a chimney. To detect moving objects, like a paraglider or helicopter, we use proprietary computer-vision and machine learning algorithms.

A customer’s yard may have clotheslines, telephone wires, or electrical wires. Wire detection is one of the hardest challenges for low-altitude flights. Through the use of computer-vision techniques we’ve invented, our drones can recognize and avoid wires as they descend into, and ascend out of, a customer’s yard.

Supply Chain Optimization

Supply chain is the process of matching between the supply of the product and demand for the product. This matching process is done through the deployment of resources: places to store the products, ways and means of transporting the product and even the ability to transform products from one form to another (e.g. transforming paper into books through printing).

Figure: Promotional video for the Amazon supply chain optimization team.

Arugably the Amazon supply chain is (or was) the largest automated decision-making system in the world in terms of the amount of money spent and the quantity of product moved through automated decision making.

Supply Chain Optimization

At the heart of an automated supply chain is the buying system, which determines the optimal stock level for products and makes purchases based on the difference between that stock level and the current stock level.

Figure: A schematic of a typical buying system for supply chain.

To make these decisions predictive models (often machine learning or statistical models) have to be moved. For example, the demand for a particular product needs to be forecast.

Forecasting

Figure: Jenny Freshwater speaking at the Amazon re:MARS event in June 2019.

The process of forecasting is described by Jenny Freshwater (at the time Director for Forecasting within Amazon’s Supply Chain Optimization team in the video in Figure \(\ref{jenny-freshwater-remars}\).

For each product in the Amazon catalogue, the demand is forecast across the a given future period.

Inventory and Buying

Forecast information is combined with predictions around lead times from suppliers, understanding of the network’s capacity (in terms of how much space is available in which fulfillment centers), the cost of storing and transporting products and the “value” for the consumer in finding the product is in stock. These models are typically operational research models (such as the “newsvendor problem” combined with machine learning and/or statistical forecasts.

Buying System

An example of a complex decision-making system might be an automated buying system. In such a system, the idea is to match demand for products to supply of products.

The matching of demand and supply is a repetitive theme for decision making systems. Not only does it occur in automated buying, but also in the allocation of drivers to riders in a ride sharing system. Or in the allocation of compute resource to users in a cloud system.

The components of any of these systems include predictions of the demand for the product, the drivers, or the compute. Predictions of the supply. Decisions are then made for how much material to keep in stock, or how many drivers to have on the road, or how much computer capacity to have in your data centers. These decisions have cost implications. The optimal amount of product will depend on the cost of making it available. For a buying system this is the storage costs.

Decisions are made based on the supply and demand to make new orders, to encourage more drivers to come into the system or to build new data centers or rent more computational power.

Figure: The components of a putative automated buying system

Monolithic System

The classical approach to building these systems was a ‘monolithic system’. Built in a similar way to the successful applications software such as Excel or Word, or large operating systems, a single code base was constructed. The complexity of such code bases run to many lines.

In practice, shared dynamically linked libraries may be used for aspects such as user interface, or networking, but the software often has many millions of lines of code. For example, the Microsoft Office suite is said to contain over 30 million lines of code.

Figure: A potential path of models in a machine learning system.

Such software is not only difficult to develop, but also to scale when computation demands increase. Amazon’s original website software (called Obidos) was a monolithic design but by the early noughties it was becoming difficult to sustain and maintain. The software was phased out in 2006 to be replaced by a modularized software known as a ‘service-oriented architecture’.

Service Oriented Architecture

In Service Oriented Architecture, or “Software as a Service” the idea is that code bases are modularized and communicate with one another using network requests. A standard approach is to use a REST API. So, rather than a single monolithic code base, the code is developed with individual services that handle the different requests.

Figure: A potential path of models in a machine learning system.

Modern software development uses an approach known as service-oriented architecture to build highly complex systems. Such systems have similar emergent properties to Conway’s “Game of Life”. Understanding these emergent properties is vitally important when diagnosing problems in the system.

Intellectual Debt

Figure: Jonathan Zittrain’s term to describe the challenges of explanation that come with AI is Intellectual Debt.

In the context of machine learning and complex systems, Jonathan Zittrain has coined the term “Intellectual Debt” to describe the challenge of understanding what you’ve created. In the ML@CL group we’ve been foucssing on developing the notion of a data-oriented architecture to deal with intellectual debt (Cabrera et al., 2023).

Zittrain points out the challenge around the lack of interpretability of individual ML models as the origin of intellectual debt. In machine learning I refer to work in this area as fairness, interpretability and transparency or FIT models. To an extent I agree with Zittrain, but if we understand the context and purpose of the decision making, I believe this is readily put right by the correct monitoring and retraining regime around the model. A concept I refer to as “progression testing”. Indeed, the best teams do this at the moment, and their failure to do it feels more of a matter of technical debt rather than intellectual, because arguably it is a maintenance task rather than an explanation task. After all, we have good statistical tools for interpreting individual models and decisions when we have the context. We can linearise around the operating point, we can perform counterfactual tests on the model. We can build empirical validation sets that explore fairness or accuracy of the model.

See Lawrence (2024) intellectual debt p. 84, 85, 349, 365.

This is the landscape we now find ourselves in with regard to software development. In practice, each of these services is often ‘owned’ and maintained by an individual team. The team is judged by the quality of their service provision. They work to detailed specifications on what their service should output, what its availability should be and other objectives like speed of response. This allows for conditional independence between teams and for faster development.

Clearly Conway’s Game of Life exhibits an enormous amount of intellectual debt, indeed that was the idea. Build something simple that exhibits great complexity. That’s what makes it so popular. But in deployed system software, intellectual debt is a major headache and emulation presents one way of dealing with it.

Unfortunately, it also makes sophisticated software systems a breeding ground for intellectual debt. Particularly when they contain components which are themselves ML components. Dealing with this challenge is a major objective of my Senior AI Fellowship at the Alan Turing Institute. You can see me talking about the problems at this recent seminar given virtually in Manchester.

Examples in Python

There are many Python resources available for different types of simulation:

• General Purpose:
  • simpy provides examples of machine shops, gas stations, car washes
  • The news vendor problem for NFL jersey orders
  • Amazon’s supply chain simulation
• Control Systems:
  • N-link pendulum using symbolic Python
  • Mountain Car in OpenAI Gym
• Scientific Computing:
  • Hodgkin-Huxley neuron models
  • Formula One race simulation
  • Computational fluid dynamics
  • Finite element analysis

There are a number of different simulations available in python, and tools specifically design for simulation. For example simpy has a list of example simulations around machine shops, gas stations, car washes.

Operations research ideas like the newsvendor problem, can also be solved, Andrea Fabry provides an example of the newsvendor problem in python for order of NFL replica jerseys here.

The news vendor problem is also a component in the Amazon supply chain. The Amazon supply chain makes predictions about supply and demand, combines them with a cost basis and computes optimal stock. Inventory orders are based on the difference between this optimal stock and current stock. The MiniSCOT simulation provides code that illustrates this.

Control problems are also systems that aim to achieve objectives given a set of parameters. A classic control problem is the inverted pendulum. This python code generalises the standard inverted pendulum using one with \(n\)-links using symbolic python code.

In reinforcement learning similar control problems are studied, a classic reinforcement learning problem is known as the Mountain Car. You can work with this problem using an environment known as OpenAI gym that includes many different reinforcement learning scenarios.

In neuroscience Hodgkin and Huxley studied the giant axon in squid to work out a set of differential equations that are still used today to model spiking neurons. Mark Kramer explains how to simulate them in python here.

All Formula One race teams simulate the race to determine their strategy (tyres, pit stops etc). While those simulations are proprietary, there is sufficient interest in the wider community that race simulations have been developed in python. Here is one that Nick Roth has made available.

Formula one teams also make use of simulation to design car parts. There are at least two components to this, simulations that allow the modelling of fluid flow across the car, and simulations that analyze the capabilities of materials under stress. You can find computational fluild dynamics simulations in python here and finite element analysis methods for computing stress in materials here.

Alongside continuous system simulation through partial differential equations, another form of simulation that arises is known as discrete event simulation. This comes up in computer networks and also in chemical systems where the approach to simulating is kown as the Gillespie algorithm.

Conclusions

We summarized the different types of simulation into roughly three groups. Firstly, those based on physical laws in the form of differential equations. Examples include certain compartmental epidemiological models, climate models and weather models. Secondly, discrete event simulations. These simulations often run to a ‘clock’, where updates to the state are taken in turns. The Game of Life is an example of this type of simulation, and Formula 1 models of race strategy also use this approach. There is another type of discrete event simulation that doesn’t use a turn-based approach but waits for the next event. The Gillespie algorithm is an example of such an approach but we didn’t cover it here. Finally, we realized that general computer code bases are also simulations. If a company has a large body of code, and particularly if it’s hosted within a streaming environment (such as Apache Kafka), it’s possible to back test the code with different inputs. Such backtests can be viewed as simulations, and in the case of large bodies of code (such as the code that manages Amazon’s automated buying systems) the back tests can be slow and could also benefit from emulation.

We’ve introduced emulation as a way of dealing with different fidelities of simulations and removing the computational demands that come with them. We’ve highlighted how emulation can be deployed and introduced the GPy software for Gaussian process modelling.

Thanks!

For more information on these subjects and more you might want to check the following resources.

• book: The Atomic Human
• twitter: @lawrennd
• podcast: The Talking Machines
• newspaper: Guardian Profile Page
• blog: http://inverseprobability.com

References