Week 3: Simulation
[jupyter][google colab][reveal]
Abstract:
This lecture will introduce the notion of simulation and review the different types of simulation we might use to represent the physical world.
Last lecture Carl Henrik introduced you to some of the challenges of approximate inference. Including the problem of mathematical tractability. Before that he introduced you to a particular form of model, the Gaussian process.
notutils
This small package is a helper package for various notebook utilities used below.
The software can be installed using
%pip install notutilsfrom the command prompt where you can access your python installation.
The code is also available on GitHub: https://github.com/lawrennd/notutils
Once notutils is installed, it can be imported in the
usual manner.
import notutilsmlai
The mlai software is a suite of helper functions for
teaching and demonstrating machine learning algorithms. It was first
used in the Machine Learning and Adaptive Intelligence course in
Sheffield in 2013.
The software can be installed using
%pip install mlaifrom the command prompt where you can access your python installation.
The code is also available on GitHub: https://github.com/lawrennd/mlai
Once mlai is installed, it can be imported in the usual
manner.
import mlai
from mlai import plotCellular Automata
Cellular automata are systems of cells that evolve according to fixed rules. The rules depend on the current state of cells and their neighbors. We’ll explore both one-dimensional (Wolfram) and two-dimensional (Conway) cellular automata. First, we’ll set up some base functionality that both types share.
These base classes and functions provide:
- A flexible grid structure that works for both 1D and 2D automata
- Consistent array access patterns
- Grid visualization tools
- Support for highlighting interesting cells or patterns
We’ll build on this foundation to implement both Wolfram’s elementary one dimensional cellular automata and later Conway’s two dimensional Game of Life.
These diagram generation functions maintain consistent styling while providing specialized visualizations for:
- Wolfram rule definitions and their outcomes
- Game of Life rules and their effects
They work with the base Grid class but provide custom layouts specific to teaching and explaining the rules of each system.
Wolfram Automata
Cellular automata are systems with simple rules that lead to complex behaviours. A simple cellular automata can be defined over one dimension of cells binary cells, and a discrete time evolution. At each time step a cell’s state is dependent on its state in a previous time step and that of its neighbours.
Stephen Wolfram noticed that such systems could be represented by a binary number that described the nature of these rules. Each cell (\(x\)) has a state at time \(t\), and the state of two neighbours (\(x+1\) and \(x-1\) at time \(t\). The cellular automata dictates what the value of that cell will be at time \(t+1\). The possible values of the cell are \(1\) or \(0\).
This simple system has eight different input states (three bits associated with the cell and its two neighbours). And two possible output states (one bit associated with the cell’s output state). so the rules of the cellular automata can be expressed by exhaustively running through the eight different input states giving the output state. To do this requires a string of eight bits (or a byte) long: one output per different input. That means there are 256 different possible cellular automata.
Wolfram numbered the different cellular automata according to the output states in an 8 bit binary number, each bit indexed by the three bits of the input states (most significant bit first). So Rule 0 would give zero output regardless of the input state. Rule 1 will give an output of 1 for the input state of three zeros etc and Rule 255 will give an output of 1 regardless of the input state.
Wolfram Automata Coding
| Pattern | Result | Binary Position | Rule Bit |
|---|---|---|---|
| ■■■ | □ | 7 | 0 |
| ■■□ | □ | 6 | 0 |
| ■□■ | □ | 5 | 0 |
| ■□□ | □ | 4 | 0 |
| □■■ | □ | 3 | 0 |
| □■□ | □ | 2 | 0 |
| □□■ | □ | 1 | 0 |
| □□□ | ■ | 0 | 1 |
The rule number 1 in binary is: 00000001
Each bit in the binary number determines the result for one of the eight possible patterns of three cells:
- A foreground square (■) represents a cell in state 1
- A background square (□) represents a cell in state 0
- The patterns are ordered from 111 (7) to 000 (0)
- The binary number determines the next state of the center cell for each pattern
For example:
- If you see pattern ‘111’ (■■■), the next state will be {‘■’ if rule_binary[0] == ‘1’ else ‘□’}
- If you see pattern ‘110’ (■■□), the next state will be {‘■’ if rule_binary[1] == ‘1’ else ‘□’}
And so on…
At each time step:
- Look at each cell and its two neighbors
- Find this pattern in the table above
- The center cell becomes the value shown in the ‘Result’ column
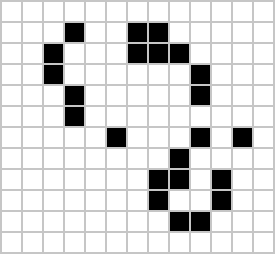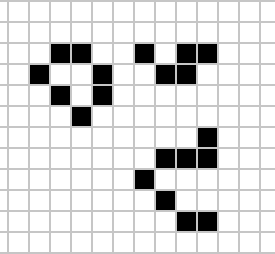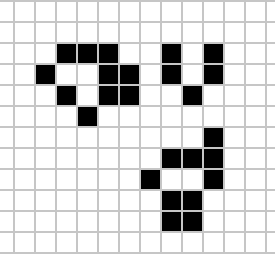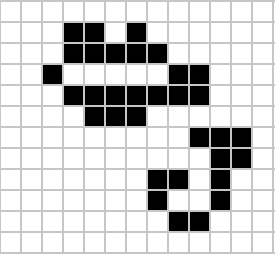
Rule 1

Figure: Rule 1 expressed in pixel form.
Rule 30
Wolfram explored exhaustively the different automata, and discovered that Rule 30 exhibited particularly interesting behaviour.
Rule 30 generates patterns that appear random, yet are completely deterministic.
| Pattern | Result | Binary Position | Rule Bit |
|---|---|---|---|
| ■■■ | □ | 7 | 0 |
| ■■□ | □ | 6 | 0 |
| ■□■ | □ | 5 | 0 |
| ■□□ | ■ | 4 | 1 |
| □■■ | ■ | 3 | 1 |
| □■□ | ■ | 2 | 1 |
| □□■ | ■ | 1 | 1 |
| □□□ | □ | 0 | 0 |
The rule number 30 in binary is: 00011110

Figure: Rule 30 expressed in pixel form. Note how mixed the output states are compared to simpler rules.
import numpy as np
import matplotlib.pyplot as pltRule 30 in Cambridge


Figure: Rule 30 has been used to decorate Cambridge North station with aluminium cladding.
But the surprising discovery I made in the 1980s by looking at things like rule 30 is that actually no such “external source” is needed: instead, it’s perfectly possible for randomness to be generated intrinsically within a system just through the process of applying definite underlying rules.
Wolfram refers to the pseudorandom pattern that emerges, in particular down the center line of the automata as “computationally irreducible”. At one point this line was even used within Wolfram as a pseudorandom number generator.
Game of Life
John Horton Conway was a mathematician who developed a game known as the Game of Life. He died in April 2020, but since he invented the game, he was in effect ‘god’ for this game. But as we will see, just inventing the rules doesn’t give you omniscience in the game.
The Game of Life is played on a grid of squares, or pixels. Each pixel is either on or off. The game has no players, but a set of simple rules that are followed at each turn the rules are.
Life Rules
John Conway’s game of life is a cellular automaton where the cells obey three very simple rules. The cells live on a rectangular grid, so that each cell has 8 possible neighbors.
|

|

Figure: ‘Death’ through loneliness in Conway’s game of life. If a cell is surrounded by less than three cells, it ‘dies’ through loneliness.
The game proceeds in turns, and at each location in the grid is either alive or dead. Each turn, a cell counts its neighbors. If there are two or fewer neighbors, the cell ‘dies’ of ‘loneliness’.
|

|

Figure: ‘Death’ through overpopulation in Conway’s game of life. If a cell is surrounded by more than three cells, it ‘dies’ through loneliness.
If there are four or more neighbors, the cell ‘dies’ from ‘overcrowding’. If there are three neighbors, the cell persists, or if it is currently dead, a new cell is born.
|

|

Figure: Birth in Conway’s life. Any position surrounded by precisely three live cells will give birth to a new cell at the next turn.
And that’s it. Those are the simple ‘physical laws’ for Conway’s game.
Game of Life Implementation
Now that we understand the rules of Life, let’s implement them. Each cell’s fate is determined by counting its eight neighbors and applying Conway’s rules.
The implementation above provides: 1. Neighbor counting with different boundary conditions 2. Rule application following Conway’s specifications 3. Support for both periodic and fixed boundaries 4. History tracking for visualization 5. Flexible initial state configuration
This base implementation will be essential when we combine it with Wolfram automata, as we’ll need to modify the boundary conditions to interact with the Wolfram rules.

Figure: Evolution of a simple oscillator (blinker) in the Game of Life.
This implementation will serve as the foundation for our exploration of Life patterns and ultimately for our hybrid system combining Life with Wolfram automata. The key is the flexibility in boundary conditions, which will allow us to interface with Wolfram rules at the edges.
Spaceships, oscillators and static patterns
The game leads to patterns emerging, some of these patterns are static, but some oscillate in place, with varying periods. Others oscillate, but when they complete their cycle they’ve translated to a new location, in other words they move. In Life the former are known as oscillators and the latter as spaceships.
Pattern Analysis
Before looking at specific examples, let’s understand how these patterns behave. Life patterns can be classified by their periodic behavior and movement: - Static patterns remain unchanged from one generation to the next - Oscillators return to their initial state after a fixed number of generations (their period) - Spaceships combine oscillation with translation, moving across the grid while cycling through their states
Each pattern can be characterized by: - Its period (how many steps before it repeats) - Its translation (how far it moves each period) - Its velocity (translation per period)
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
John Horton Conway, as the creator of the game of life, could be seen
somehow as the god of this small universe. He created the rules. The
rules are so simple that in many senses he, and we, are all-knowing in
this space. But despite our knowledge, this world can still ‘surprise’
us. From the simple rules, emergent patterns of behaviour arise.

|

|

Figure: Left A Glider pattern discovered 1969 by Richard K. Guy. Right. John Horton Conway, creator of Life (1937-2020). The glider is an oscillator that moves diagonally after creation.
The glider was ‘discovered’ in 1969 by Richard K. Guy. What do we mean by discovered in this context? Well, as soon as the game of life is defined, objects such as the glider do somehow exist, but the many configurations of the game mean that it takes some time for us to see one and know it exists. This means, that despite being the creator, Conway, and despite the rules of the game being simple, and despite the rules being deterministic, we are not ‘omniscient’ in any simplistic sense. It requires computation to ‘discover’ what can exist in this universe once it’s been defined.


Figure: The Gosper glider gun is a configuration that creates gliders. A new glider is released after every 30 turns.
These patterns had to be discovered, in the same way that a scientist might discover a disease, or an explorer a new land. For example, the Gosper glider gun was discovered by Bill Gosper in 1970. It is a pattern that creates a new glider every 30 turns of the game.

|

|

Figure: Left A Loafer pattern discovered by Josh Ball in 2013. Right. John Horton Conway, creator of Life (1937-2020).
Despite widespread interest in Life, some of its patterns were only very recently discovered like the Loafer, discovered in 2013 by Josh Ball. So, despite the game having existed for over forty years, and the rules of the game being simple, there are emergent behaviors that are unknown.
Once these patterns are discovered, they are combined (or engineered) to create new Life patterns that do some remarkable things. For example, there’s a life pattern that runs a Turing machine, or more remarkably there’s a Life pattern that runs Life itself.


Figure: The Game of Life running in Life. The video is drawing out recursively showing pixels that are being formed by filling cells with moving spaceships. Each individual pixel in this game of life is made up of \(2048 \times 2048\) pixels called an OTCA metapixel.
To find out more about the Game of Life you can watch this video by Alan Zucconi or read his associated blog post.

Figure: An introduction to the Game of Life by Alan Zucconi.
Contrast this with our situation where in ‘real life’ we don’t know the simple rules of the game, the state space is larger, and emergent behaviors (hurricanes, earthquakes, volcanos, climate change) have direct consequences for our daily lives, and we understand why the process of ‘understanding’ the physical world is so difficult. We also see immediately how much easier we might expect the physical sciences to be than the social sciences, where the emergent behaviors are contingent on highly complex human interactions.
include{_simulation/includes/automata-base.md}
Combining Wolfram and Conway
We can create an interesting hybrid system by combining Wolfram’s elementary cellular automata with Conway’s Game of Life. The system consists of a square grid where the interior follows Conway’s rules, but the border cells evolve according to a chosen Wolfram rule. The Wolfram rule wraps around the border, creating a dynamic boundary condition for the Life cells.
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimationLet’s demonstrate this hybrid system with some examples. First, let’s see how Rule 30 interacts with a glider:


Figure: A glider pattern evolving within borders governed by Rule 30. Notice how the complex border patterns influence the glider’s behavior.
Now let’s try a different combination - Rule 110 (another complex rule) with a loafer:


Figure: A loafer pattern evolving within borders governed by Rule 110. The border patterns create a dynamic environment that affects the loafer’s movement.
This hybrid system demonstrates how two different types of cellular automata can be combined to create new behaviours.
Packing Problems


Figure: Packing 9 squares into a single square. This example is trivially solved. Credit https://erich-friedman.github.io/packing/
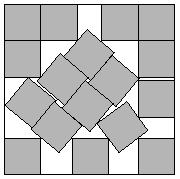

Figure: Packing 17 squares into a single square. The optimal solution is sometimes hard to find. Here the side length of the smallest square that holds 17 similarly shaped squares is at least 4.675 times the smaller square. This solution found by John Bidwell in 1997. Credit https://erich-friedman.github.io/packing/
Another example of a problem where the “physics” is understood because it’s really mathematics, is packing problems. Here the mathematics is just geometry, but still we need some form of compute to solve these problems. Erich Friedman’s website contains a host of these problems, only some of which are analytically tractable.
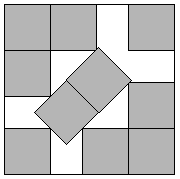

Figure: Packing 10 squares into a single square. This example is proven by Walter Stromquist (Stromquist, 1984). Here \(s=3+\frac{1}{\sqrt{2}}\). Credit https://erich-friedman.github.io/packing/
Bayesian Inference by Rejection Sampling
One view of Bayesian inference is to assume we are given a mechanism for generating samples, where we assume that mechanism is representing an accurate view on the way we believe the world works.
This mechanism is known as our prior belief.
We combine our prior belief with our observations of the real world by discarding all those prior samples that are inconsistent with our observations. The likelihood defines mathematically what we mean by inconsistent with the observations. The higher the noise level in the likelihood, the looser the notion of consistent.
The samples that remain are samples from the posterior.
This approach to Bayesian inference is closely related to two sampling techniques known as rejection sampling and importance sampling. It is realized in practice in an approach known as approximate Bayesian computation (ABC) or likelihood-free inference.
In practice, the algorithm is often too slow to be practical, because most samples will be inconsistent with the observations and as a result the mechanism must be operated many times to obtain a few posterior samples.
However, in the Gaussian process case, when the likelihood also assumes Gaussian noise, we can operate this mechanism mathematically, and obtain the posterior density analytically. This is the benefit of Gaussian processes.
First, we will load in two python functions for computing the covariance function.
Next, we sample from a multivariate normal density (a multivariate Gaussian), using the covariance function as the covariance matrix.


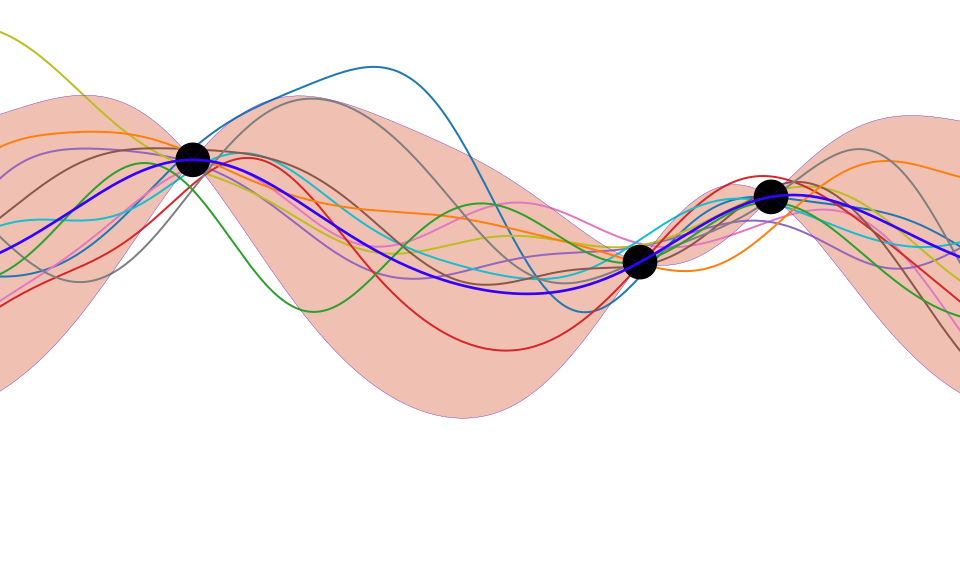

Figure: One view of Bayesian inference is we have a machine for generating samples (the prior), and we discard all samples inconsistent with our data, leaving the samples of interest (the posterior). This is a rejection sampling view of Bayesian inference. The Gaussian process allows us to do this analytically by multiplying the prior by the likelihood.
So, Gaussian processes provide an example of a particular type of model. Or, scientifically, we can think of such a model as a mathematical representation of a hypothesis around data. The rejection sampling view of Bayesian inference can be seen as rejecting portions of that initial hypothesis that are inconsistent with the data. From a Popperian perspective, areas of the prior space are falsified by the data, leaving a posterior space that represents remaining plausible hypotheses.
The flaw with this point of view is that the initial hypothesis space was also restricted. It only contained functions where the instantiated points from the function are jointly Gaussian distributed.
Universe isn’t as Gaussian as it Was
The Planck space craft was a European Space Agency space telescope that mapped the cosmic microwave background (CMB) from 2009 to 2013. The Cosmic Microwave Background is the first observable echo we have of the big bang. It dates to approximately 400,000 years after the big bang, at the time the Universe was approximately \(10^8\) times smaller and the temperature of the Universe was high, around \(3 \times 10^8\) degrees Kelvin. The Universe was in the form of a hydrogen plasma. The echo we observe is the moment when the Universe was cool enough for protons and electrons to combine to form hydrogen atoms. At this moment, the Universe became transparent for the first time, and photons could travel through space.


Figure: Artist’s impression of the Planck spacecraft which measured the Cosmic Microwave Background between 2009 and 2013.
The objective of the Planck spacecraft was to measure the anisotropy and statistics of the Cosmic Microwave Background. This was important, because if the standard model of the Universe is correct the variations around the very high temperature of the Universe of the CMB should be distributed according to a Gaussian process.1 Currently our best estimates show this to be the case (Elsner et al., 2016, 2015; Jaffe et al., 1998; Pontzen and Peiris, 2010).
To the high degree of precision that we could measure with the Planck space telescope, the CMB appears to be a Gaussian process. The parameters of its covariance function are given by the fundamental parameters of the Universe, for example the amount of dark matter and matter in the Universe.
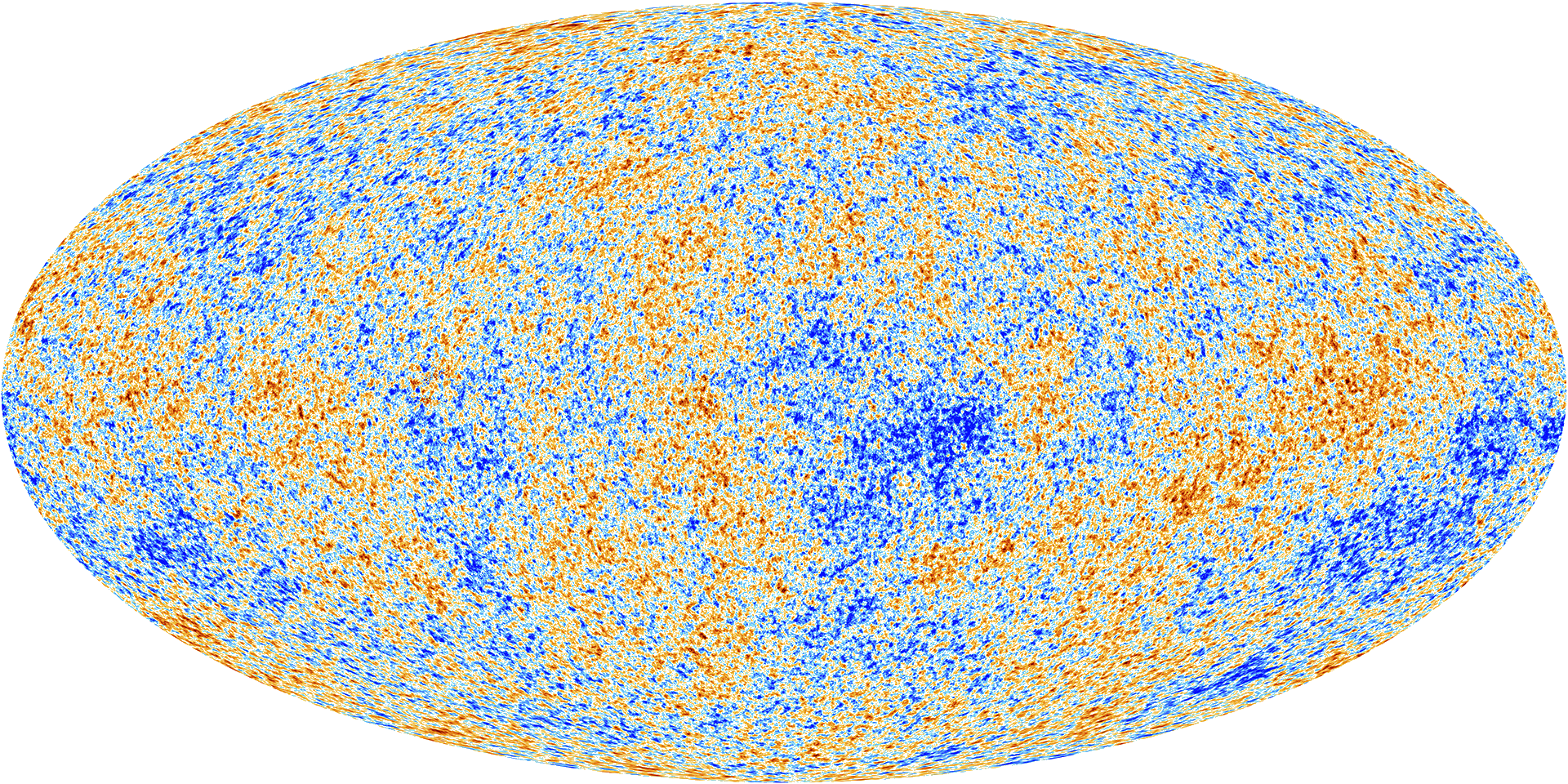

Figure: The cosmic microwave background is, to a very high degree of precision, a Gaussian process. The parameters of its covariance function are given by fundamental parameters of the universe, such as the amount of dark matter and mass.
Simulating a CMB Map
The simulation was created by Boris Leistedt, see the original Jupyter notebook here.
Here we use that code to simulate our own universe and sample from what it looks like.
First, we install some specialist software as well as
matplotlib, scipy, numpy we
require
%pip install camb%pip install healpyimport healpy as hp
import camb
from camb import model, initialpowerNow we use the theoretical power spectrum to design the covariance function.
nside = 512 # Healpix parameter, giving 12*nside**2 equal-area pixels on the sphere.
lmax = 3*nside # band-limit. Should be 2*nside < lmax < 4*nside to get information content.Now we design our Universe. It is parameterized according to the \(\Lambda\)CDM model. The variables are
as follows. H0 is the Hubble parameter (in Km/s/Mpc). The
ombh2 is Physical Baryon density parameter. The
omch2 is the physical dark matter density parameter.
mnu is the sum of the neutrino masses (in electron Volts).
omk is the \(\Omega_k\) is
the curvature parameter, which is here set to 0, giving the minimal six
parameter Lambda-CDM model. tau is the reionization optical
depth.
Then we set ns, the “scalar spectral index”. This was
estimated by Planck to be 0.96. Then there’s r, the ratio
of the tensor power spectrum to scalar power spectrum. This has been
estimated by Planck to be under 0.11. Here we set it to zero. These
parameters are associated with
inflation.
# Mostly following http://camb.readthedocs.io/en/latest/CAMBdemo.html with parameters from https://en.wikipedia.org/wiki/Lambda-CDM_model
pars = camb.CAMBparams()
pars.set_cosmology(H0=67.74, ombh2=0.0223, omch2=0.1188, mnu=0.06, omk=0, tau=0.066)
pars.InitPower.set_params(ns=0.96, r=0)Having set the parameters, we now use the python software “Code for Anisotropies in the Microwave Background” to get the results.
pars.set_for_lmax(lmax, lens_potential_accuracy=0);
results = camb.get_results(pars)
powers = results.get_cmb_power_spectra(pars)
totCL = powers['total']
unlensedCL = powers['unlensed_scalar']
ells = np.arange(totCL.shape[0])
Dells = totCL[:, 0]
Cells = Dells * 2*np.pi / ells / (ells + 1) # change of convention to get C_ell
Cells[0:2] = 0cmbmap = hp.synfast(Cells, nside,
lmax=lmax, mmax=None, alm=False, pol=False,
pixwin=False, fwhm=0.0, sigma=None, new=False, verbose=True)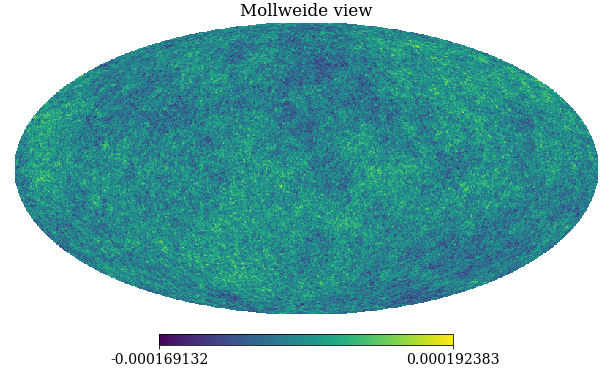

Figure: A simulation of the Cosmic Microwave Background obtained through sampling from the relevant Gaussian process covariance (in polar co-ordinates).
The world we see today, of course, is not a Gaussian process. There are many discontinuities, for example, in the density of matter, and therefore in the temperature of the Universe.
 \(=f\Bigg(\)
\(=f\Bigg(\) \(\Bigg)\)
\(\Bigg)\)

Figure: What we observe today is some non-linear function of the cosmic microwave background.
We can think of today’s observed Universe, though, as a being a consequence of those temperature fluctuations in the CMB. Those fluctuations are only order \(10^{-6}\) of the scale of the overall temperature of the Universe. But minor fluctuations in that density are what triggered the pattern of formation of the Galaxies. They determined how stars formed and created the elements that are the building blocks of our Earth (Vogelsberger et al., 2020).
The Universe isn’t as Gaussian as it Was
Those cosmological simulations are based on a relatively simple set of ‘rules’ that stem from our understanding of natural laws. These ‘rules’ are mathematical abstractions of the physical world. Representations of behavior in mathematical form that capture the interaction forces between particles. The grand aim of physics has been to unify these rules into a single unifying theory. Popular understanding of this quest developed because of Stephen Hawking’s book, “A Brief History of Time”. The idea of these laws as ‘ultimate causes’ has given them a pseudo religious feel, see for example Paul Davies’s book “The Mind of God” which comes from a quotation form Stephen Hawking.
If we do discover a theory of everything … it would be the ultimate triumph of human reason-for then we would truly know the mind of God
Stephen Hawking in A Brief History of Time 1988
Precise Physical Laws
We’ve already reviewed the importance of Newton’s laws in forging our view of science: we mentioned the influence Christiaan Huygens’ work on collisions had on Daniel Bernoulli in forming the kinetic theory of gases. These ideas inform many of the physical models we have today around a number of natural phenomena. The MET Office supercomputer in Exeter spends its mornings computing the weather across the world its afternoons modelling climate scenarios. It uses the same set of principles that Newton described, and Bernoulli explored for gases. They are encoded in the Navier-Stokes equations. Differential equations that govern the flow of compressible and incompressible fluids. As well as predicting our weather, these equations are used in fluid dynamics models to understand the flight of aircraft, the driving characteristics of racing cars and the efficiency of gas turbine engines.
Abstraction and Emergent Properties

Figure: A scale of different simulations we might be interested in when modelling the physical world. The scale is \(\log_{10}\) meters. The scale reflects something about the level of granularity where we might choose to know “all positions of all items of which nature is composed”.
Unfortunately, even if such an equation were to exist, we would be unlikely to know “all positions of all items of which nature is composed”. A good example here is computational systems biology. In that domain we are interested in understanding the underlying function of the cell. These systems sit somewhere between the two extremes that Laplace described: “the movements of the greatest bodies of the universe and those of the smallest atom”.
When the smallest atom is considered, we need to introduce uncertainty. We again turn to a different work of Maxwell, building on Bernoulli’s kinetic theory of gases we end up with probabilities for representing the location of the ‘molecules of air’. Instead of a deterministic location for these particles we represent our belief about their location in a distribution.
Computational systems biology is a world of micro-machines, built of three dimensional foldings of strings of proteins. There are spindles (stators) and rotors (e.g. ATP Synthase), there are small copying machines (e.g. RNA Polymerase) there are sequence to sequence translators (Ribosomes). The cells store information in DNA but have an ecosystem of structures and messages being built and sent in proteins and RNA. Unpicking these structures has been a major preoccupation of biology. That is knowing where the atoms of these molecules are in the structure, and how the parts of the structure move when these small micro-machines are carrying out their roles.
We understand most (if not all) of the physical laws that drive the movements of these molecules, but we don’t understand all the actions of the cell, nor can we intervene reliably to improve things. So, even in the case where we have a good understanding of the physical laws, Laplace’s gremlin emerges in our knowledge of “the positions of all items of which nature is composed”.
Molecular Dynamics Simulations
By understanding and simulating the physics, we can recreate operations that are happening at the level of proteins in the human cell. V-ATPase is an enzyme that pumps protons. But at the microscopic level it’s a small machine. It produces ATP in response to a proton gradient. A paper in Science Advances (Roh et al., 2020) simulates the functioning of these proteins that operate across the cell membrane. This makes these proteins difficult to crystallize, the response to this challenge is to use a simulation which (somewhat) abstracts the processes. You can also check this blog post from the paper’s press release.
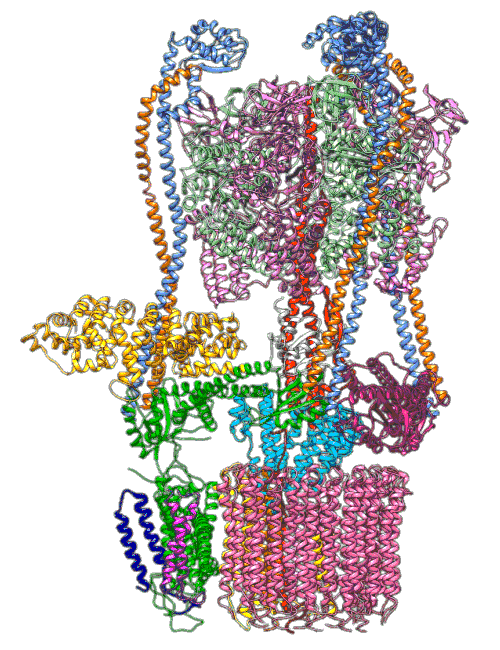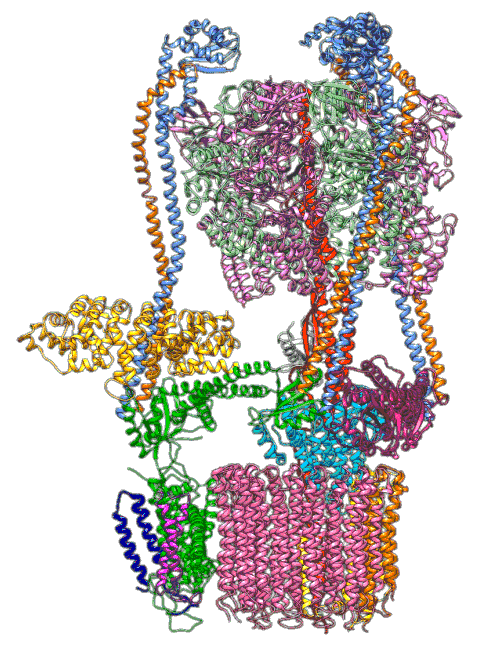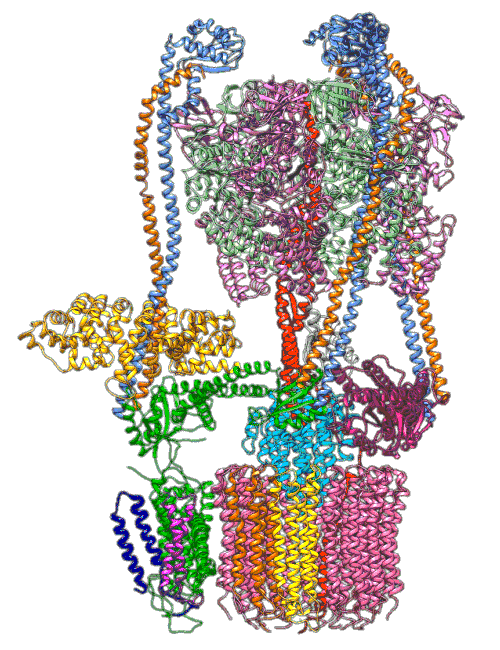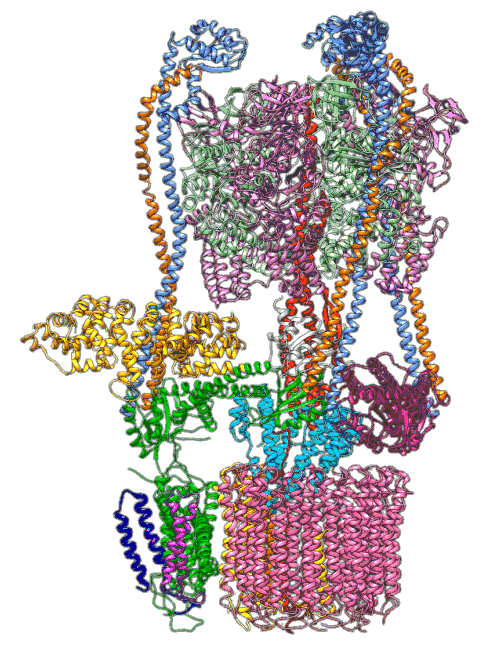

Figure: The V-ATPase enzyme pumps proteins across membranes. This molecular dynamics simulation was published in Science Advances (Roh et al., 2020). The scale is roughly \(10^{-8} m\).
Quantum Mechanics
Alternatively, we can drop down a few scales and consider simulation of the Schrödinger equation. Intractabilities in the many-electron Schrödinger equation have been addressed using deep neural networks to speed up the solution enabling simulation of chemical bonds (Pfau et al., 2020). The PR-blog post is also available. The paper uses a neural network to model the quantum state of a number of electrons.
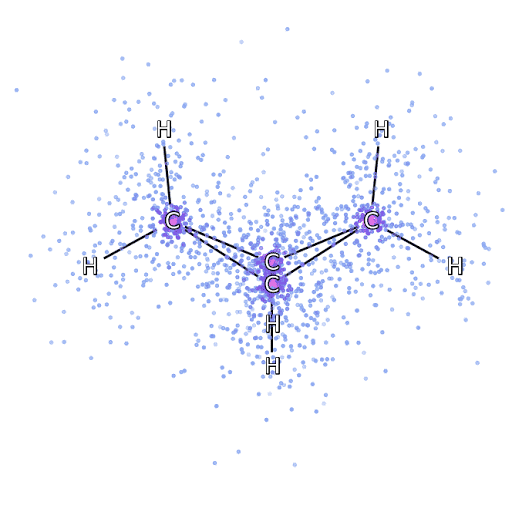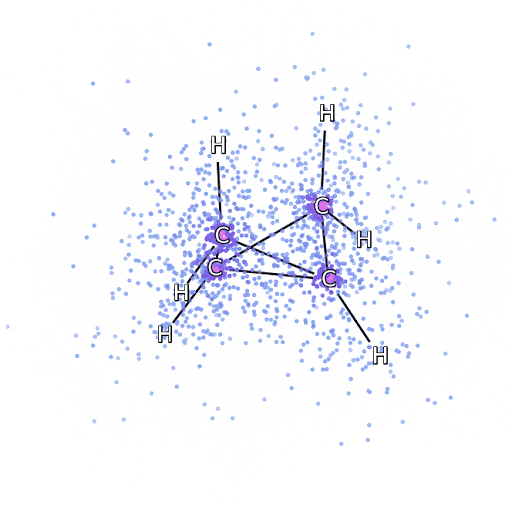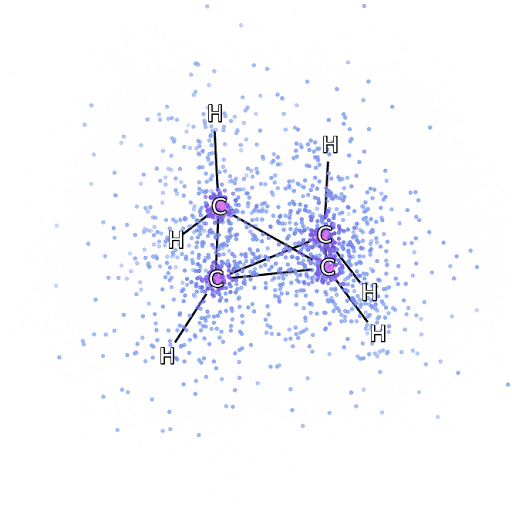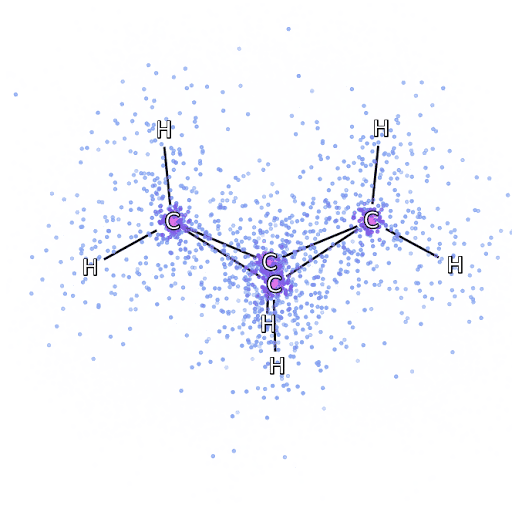

Figure: The many-electron Schrödinger equation is important in understanding how Chemical bonds are formed.
Each of these simulations have the same property of being based on a set of (physical) rules about how particles interact. But one of the interesting characteristics of such systems is how the properties of the system are emergent as the dynamics are allowed to continue.
These properties cannot be predicted without running the physics, or the equivalently the equation. Computation is required. And often the amount of computation that is required is prohibitive.
How Machine Learning Can Help
Machine learning models can often capture some of the regularities of the system that we find in these emergent properties. They do so, not from first principles, but from analysis of the data. In the Atomic Human, I argue that this has more in common with how human intellience solves problems than through first-principles modelling. When it comes to ML and the Physical World, the aim is to use machine learning models alongside simulations to get the best of both worlds.
See Lawrence (2024) hooshing, Pooh’s law of p. 157-158,160.
Conclusion
We’ve introduced the notion of a simulator. A body of computer code that expresses our understanding of a particular physical system. We introduced such simulators through physical laws, such as laws of gravitation or electro-magnetism. But we soon saw that in many simulations those laws become abstracted, and the simulation becomes more phenomological.
Even full knowledge of all laws does not give us access to ‘the mind of God’, because we are lacking information about the data, and we are missing the compute. These challenges further motivate the need for abstraction, and we’ve seen examples of where such abstractions are used in practice.
The example of Conway’s Game of Life highlights how complex emergent phenomena can require significant computation to explore.
Thanks!
For more information on these subjects and more you might want to check the following resources.
- book: The Atomic Human
- twitter: @lawrennd
- podcast: The Talking Machines
- newspaper: Guardian Profile Page
- blog: http://inverseprobability.com

