Simulation

Neil D. Lawrence

Cellular Automata

Wolfram Automata

Wolfram Automata Coding

Pattern Result Binary Position Rule Bit
■■■ □ 7 0
■■□ □ 6 0
■□■ □ 5 0
■□□ □ 4 0
□■■ □ 3 0
□■□ □ 2 0
□□■ □ 1 0
□□□ ■ 0 1

The rule number 1 in binary is: 00000001

Wolfram Automata Coding

Each bit in the binary number determines the result for one of the eight possible patterns of three cells:

  • A foreground square (■) represents a cell in state 1
  • A background square (□) represents a cell in state 0
  • The patterns are ordered from 111 (7) to 000 (0)
  • The binary number determines the next state of the center cell for each pattern

Wolfram Automata Coding

For example:

  • If you see pattern ‘111’ (■■■), the next state will be {‘■’ if rule_binary[0] == ‘1’ else ‘□’}
  • If you see pattern ‘110’ (■■□), the next state will be {‘■’ if rule_binary[1] == ‘1’ else ‘□’}

And so on…

Wolfram Automata Coding

At each time step:

  1. Look at each cell and its two neighbors
  2. Find this pattern in the table above
  3. The center cell becomes the value shown in the ‘Result’ column

Rule 1

Rule 30

Pattern Result Binary Position Rule Bit
■■■ □ 7 0
■■□ □ 6 0
■□■ □ 5 0
■□□ ■ 4 1
□■■ ■ 3 1
□■□ ■ 2 1
□□■ ■ 1 1
□□□ □ 0 0

The rule number 30 in binary is: 00011110

Rule 30

Rule 30 in Cambridge

Game of Life

Loneliness
loneliness

Crowding
overcrowding

Birth
birth

Game of Life Implementation

Spaceships, oscillators and static patterns

Pattern Analysis


Glider

Glider (1969)

Gosper Glider Gun

Loafer

Loafer (2013)

include{_simulation/includes/automata-base.md}

Combining Wolfram and Conway

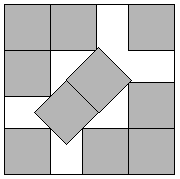
Packing Problems

Packing Problems

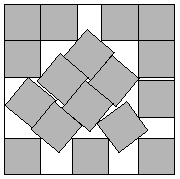
Packing Problems

\(=f\Bigg(\)\(\Bigg)\)

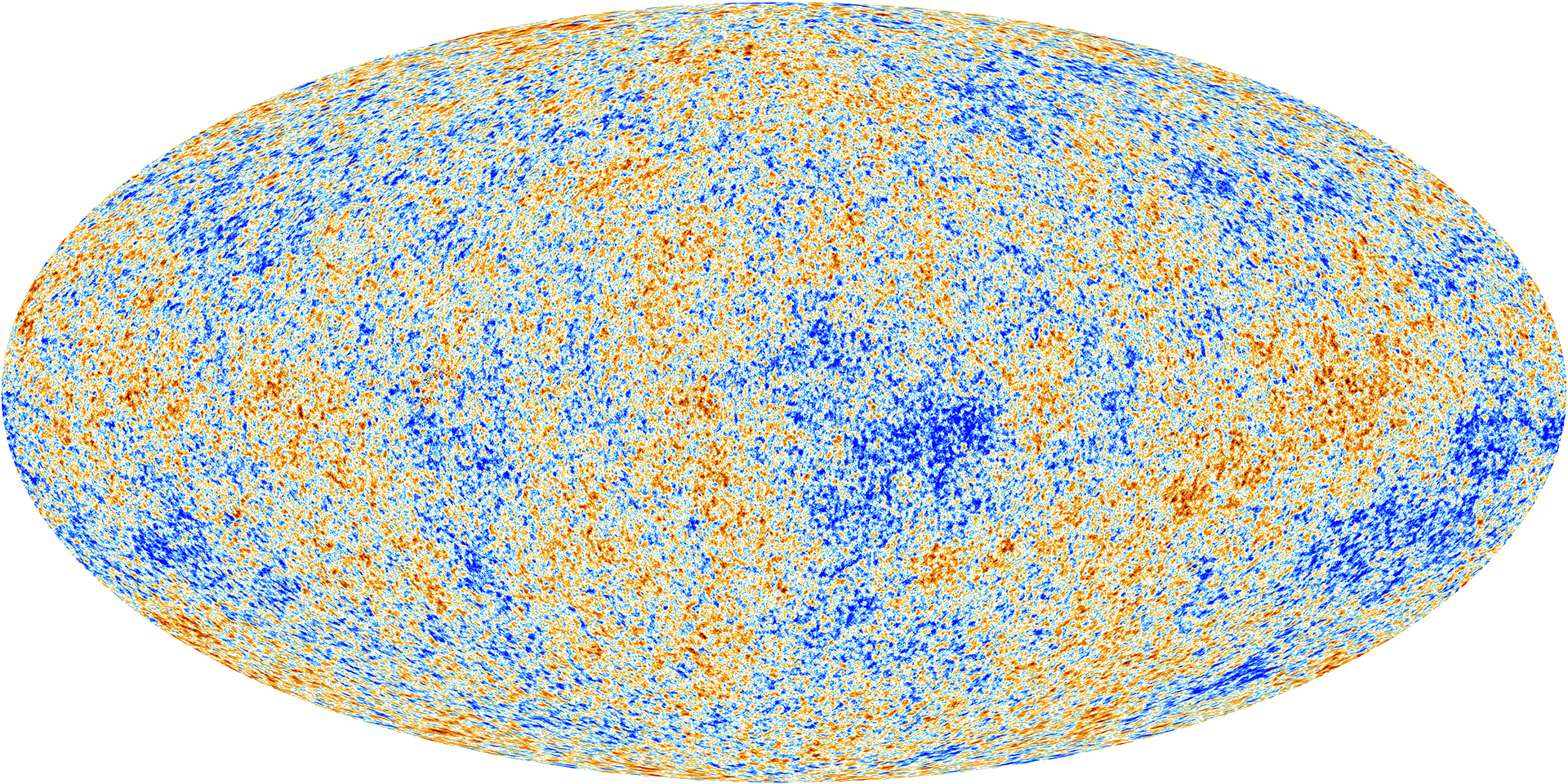
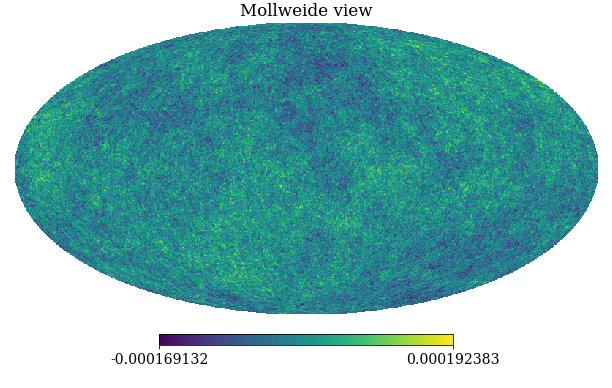
The Universe isn’t as Gaussian as it Was

If we do discover a theory of everything … it would be the ultimate triumph of human reason-for then we would truly know the mind of God

Stephen Hawking in A Brief History of Time 1988

Precise Physical Laws

  • Newton’s laws
  • Huygens and conservation of energy
  • Daniel Bernoulli and the kinetic theory of gases
  • Modern climate simulation and Navier-Stokes equations

Abstraction and Emergent Properties

Abstraction

  • We often abstract smaller scales away e.g. in statistical mechanics.
  • When we’re abstracting finer length scales we can introduce uncertainties.
    • E.g. Maxwell-Boltzmann distribution for ideal Gas.

Emergence

  • But fine scale local-laws also lead to emergent properties.
  • Some of these properties exist at large scale.
  • In particular, when there are complex interactions between molecules.

Molecular Dynamics Simulations

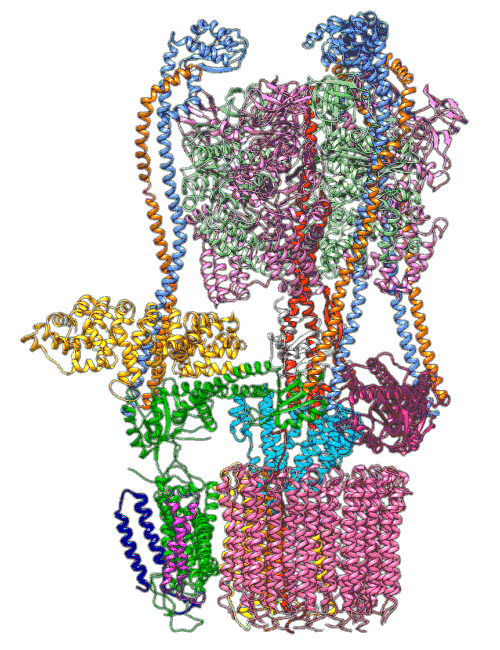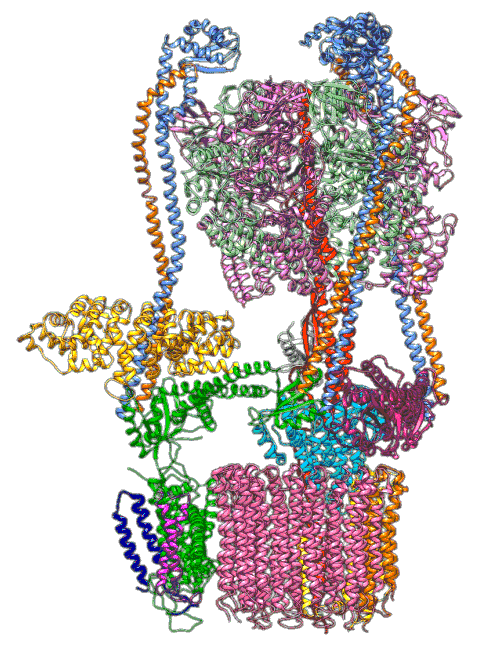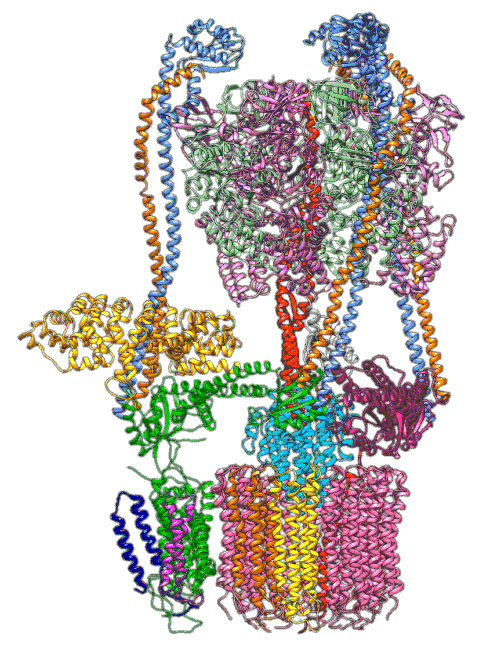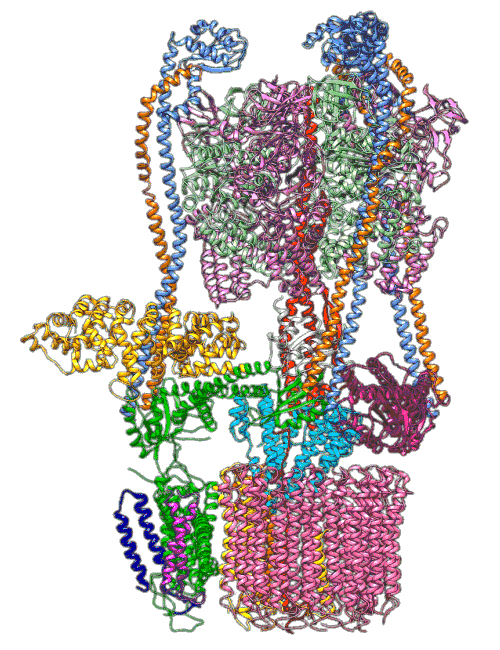
Quantum Mechanics

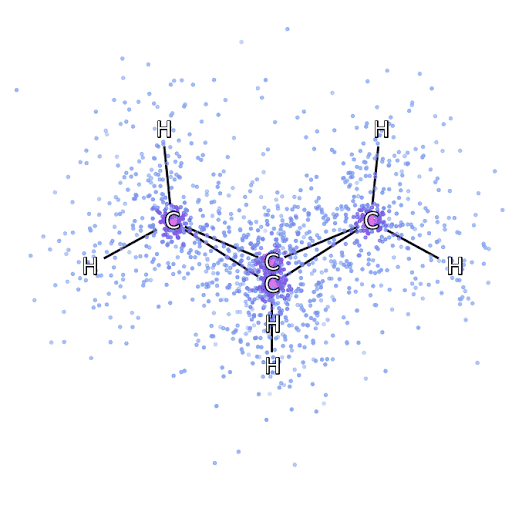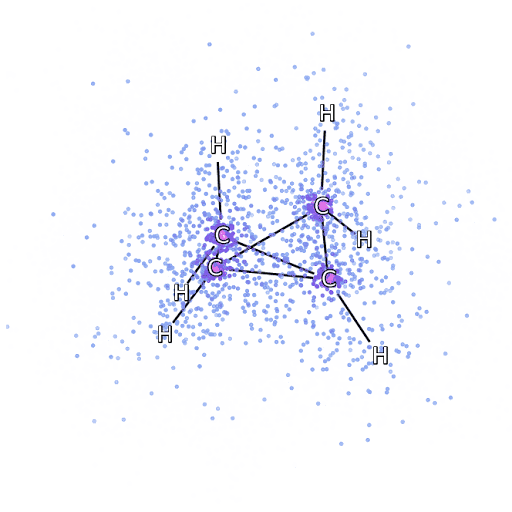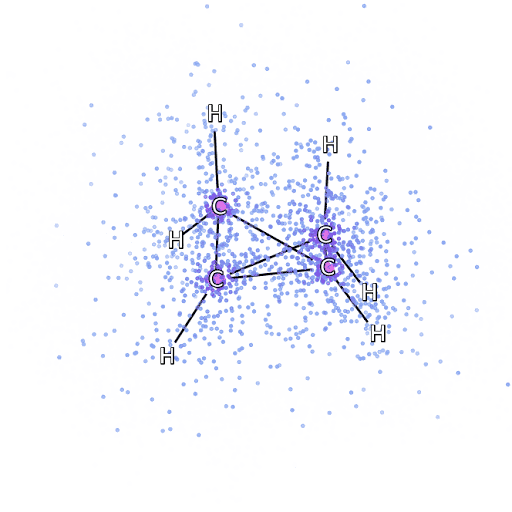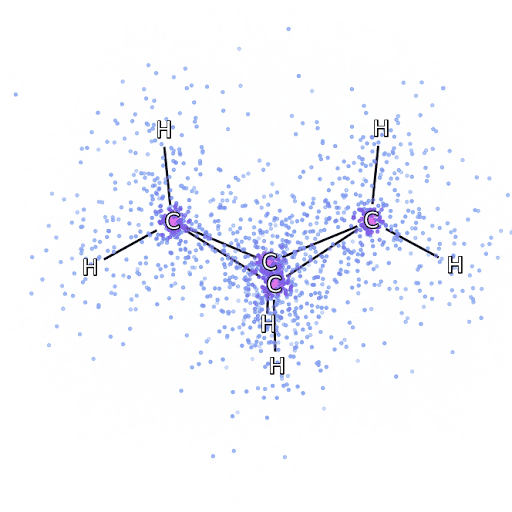
How Machine Learning Can Help

Conclusion

  • Introduced simulator: body of computer code.
  • Emergent properties
  • Abstractions
  • Levels of fidelity

Thanks!

References

Roh, S.-H., Shekhar, M., Pintilie, G., Chipot, C., Wilkens, S., Singharoy, A., Chiu, W., 2020. Cryo-EM and MD infer water-mediated proton transport and autoinhibition mechanisms of Vo complex. Science Advances 6. https://doi.org/10.1126/sciadv.abb9605
Stromquist, W.R., 1984. Packing unit squares inside squares, III. Daniel H. Wagner Associates.