Week 2: Generalised Linear Models

[jupyter][google colab][reveal]

Neil D. Lawrence

Abstract:

ML Foundations Course Notebook Setup

We install some bespoke codes for creating and saving plots as well as loading data sets.

%%capture
%pip install notutils
%pip install pods
%pip install mlai

import notutils
import pods
import mlai
import mlai.plot as plot

Learning Objectives

• Understand the GLM framework: linear predictor, link and inverse-link.
• Derive logistic regression from Bernoulli with log-odds (logit) link.
• Implement prediction, likelihood, and gradient for logistic regression.
• Contrast logistic regression updates with the perceptron; interpret decision boundaries.
• Build and use design matrices; run batch and stochastic gradient descent on a real dataset (NMIS).
• Use statsmodels for linear and logistic regression, and interpret diagnostics.
• Extend to multiclass via softmax (categorical) regression and its objective.
• Model counts with Poisson regression and log link; recognise multiplicative effects.
• Connect GLMs to the exponential family and canonical links.
• Apply practical modeling tips: feature engineering, validation, diagnostics.

Lecture Timing

• Review — 5 min
• GLM framing (conditional modeling, link functions) — 8 min
• Logistic regression: prediction & likelihood — 12 min
• Optimisation & perceptron comparison — 10 min
• Toy data and design matrices — 8 min
• Nigeria NMIS logistic regression (batch/SGD, weights) — 10 min
• statsmodels: linear and logistic demos — 10 min
• Multiclass (softmax) regression — 8 min
• Poisson regression & exponential family — 12 min
• Practical tips and Q&A — 7 min

Review

We introduced machine learning as a way to extract knowledge from data to make predictions through a prediction function and an objective function. We looked at a simple example of predicting whether someone would buy a jumper based on their age and latitude, using logistic regression to model the log-odds of purchase. This highlighted how machine learning can codify predictions through mathematical functions. This is an example of a broader approach known as generalised linear models.

When taking a probabilistic approach to supervised learning we’re interested in predicting a class label, \(y_i\), given an input, \(\mathbf{ x}_i\). That’s represented probabilisticially as \(p(y_i|\mathbf{ x}_i)\). We can derive this conditional distribution through either (1) modelling the joint distribution, \(p(\mathbf{ y}, \mathbf{X})\) and then dividing by the marginal distribution of the inputs, \(p(\mathbf{X})\) , or (2) focusing specifically on modeling the conditional density, \(p(\mathbf{ y}|\mathbf{X})\), that directly answers our prediction question. In the generalised linear model we choose the second approach.

As we move to generalised linear models like logistic regression, we’ll see how directly modeling the conditional density \(p(\mathbf{ y}|\mathbf{X})\) can provide more flexibility in our modeling assumptions, while still allowing us to make the specific predictions we need.

Logistic Regression

A logistic regression is an approach to classification which extends the linear regression models we’ve already explored. Rather than modeling the output of the function directly the assumption is that we model the log-odds with the basis functions.

The odds are defined as the ratio of the probability of a positive outcome, to the probability of a negative outcome. Just as we saw in our jumper (sweater) example where \[ \log \frac{p(\text{bought})}{p(\text{not bought})} = w_0 + w_1 \text{age} + w_2 \text{latitude} \] If the probability of a positive outcome is denoted by \(\pi\), then the odds are computed as \(\frac{\pi}{1-\pi}\).

Odds are widely used by bookmakers in gambling, although a bookmakers odds won’t normalise: i.e. if you look at the equivalent probabilities, and sum over the probability of all outcomes the bookmakers are considering, then you won’t get one. This is how the bookmaker makes a profit. Because a probability is always between zero and one, the odds are always between \(0\) and \(\infty\). If the positive outcome is unlikely the odds are close to zero, if it is very likely then the odds become close to infinite. Taking the logarithm of the odds maps the odds from the positive half space to being across the entire real line. Odds that were between 0 and 1 (where the negative outcome was more likely) are mapped to the range between \(-\infty\) and \(0\). Odds that are greater than 1 are mapped to the range between \(0\) and \(\infty\). Considering the log odds therefore takes a number between 0 and 1 (the probability of positive outcome) and maps it to the entire real line. The function that does this is known as the logit function, \(g(p_i) = \log\frac{p_i}{1-p_i}\). This function is known as a link function.

For a standard regression we take, \[ f(\mathbf{ x}) = \mathbf{ w}^\top \boldsymbol{ \phi}(\mathbf{ x}), \] if we want to perform classification we perform a logistic regression. \[ \log \frac{\pi}{(1-\pi)} = \mathbf{ w}^\top \boldsymbol{ \phi}(\mathbf{ x}) \] where the odds ratio between the positive class and the negative class is given by \[ \frac{\pi}{(1-\pi)} \] The odds can never be negative, but can take any value from 0 to \(\infty\). We have defined the link function as taking the form \(g^{-1}(\cdot)\) implying that the inverse link function is given by \(g(\cdot)\). Since we have defined, \[ g(\pi) = \mathbf{ w}^\top \boldsymbol{ \phi}(\mathbf{ x}) \] we can write \(\pi\) in terms of the inverse link function, \(h(\cdot)\) as \[ \pi = h(\mathbf{ w}^\top \boldsymbol{ \phi}(\mathbf{ x})). \]

We’ll define our prediction, objective and gradient functions below. But before we start, we need to define a basis function for our model. Let’s start with the linear basis.

import numpy as np

import mlai

from mlai import linear

Sigmoid Function

Figure: The logistic function.

The function has this characeristic ‘s’-shape (from where the term sigmoid, as in sigma, comes from). It also takes the input from the entire real line and ‘squashes’ it into an output that is between zero and one. For this reason it is sometimes also called a ‘squashing function.’

The sigmoid comes from the inverting the odds ratio, \[ \frac{\pi}{(1-\pi)} \] where \(\pi\) is the probability of a positive outcome and \(1-\pi\) is the probability of a negative outcome

Prediction Function

Now we have the basis function let’s define the prediction function.

import numpy as np

def predict(w, x, basis=mlai.linear, **kwargs):
    "Generates the prediction function and the basis matrix."
    Phi = basis(x, **kwargs)
    f = np.dot(Phi, w)
    return 1./(1+np.exp(-f)), Phi

This inverse of the link function is known as the logistic (thus the name logistic regression) or sometimes it is called the sigmoid function. For a particular value of the input to the link function, \(f_i = \mathbf{ w}^\top \boldsymbol{ \phi}(\mathbf{ x}_i)\) we can plot the value of the inverse link function as below.

By replacing the inverse link with the sigmoid we can write \(\pi\) as a function of the input and the parameter vector as, \[ \pi(\mathbf{ x},\mathbf{ w}) = \frac{1}{1+\exp\left(-\mathbf{ w}^\top \boldsymbol{ \phi}(\mathbf{ x})\right)}. \] The process for logistic regression is as follows. Compute the output of a standard linear basis function composition (\(\mathbf{ w}^\top \boldsymbol{ \phi}(\mathbf{ x})\), as we did for linear regression) and then apply the inverse link function, \(g(\mathbf{ w}^\top \boldsymbol{ \phi}(\mathbf{ x}))\). In logistic regression this involves squashing it with the logistic (or sigmoid) function. Use this value, which now has an interpretation as a probability in a Bernoulli distribution to form the likelihood. Then we can assume conditional independence of each data point given the parameters and develop a likelihod for the entire data set.

The Bernoulli likelihood is of the form, \[ P(y_i|\mathbf{ w}, \mathbf{ x}) = \pi_i^{y_i} (1-\pi_i)^{1-y_i} \] which we can think of as clever trick for mathematically switching between two probabilities if we were to write it as code it would be better described as

def bernoulli(x, y, pi):
    if y == 1:
        return pi(x)
    else:
        return 1-pi(x)

but writing it mathematically makes it easier to write our objective function within a single mathematical equation.

Maximum Likelihood

To obtain the parameters of the model, we need to maximise the likelihood, or minimise the objective function, normally taken to be the negative log likelihood. With a data conditional independence assumption the likelihood has the form, \[ P(\mathbf{ y}|\mathbf{ w}, \mathbf{X}) = \prod_{i=1}^nP(y_i|\mathbf{ w}, \mathbf{ x}_i). \] which can be written as a log likelihood in the form \[ \log P(\mathbf{ y}|\mathbf{ w}, \mathbf{X}) = \sum_{i=1}^n\log P(y_i|\mathbf{ w}, \mathbf{ x}_i) = \sum_{i=1}^n y_i \log \pi_i + \sum_{i=1}^n(1-y_i)\log (1-\pi_i) \] and if we take the probability of positive outcome for the \(i\)th data point to be given by \[ \pi_i = h\left(\mathbf{ w}^\top \boldsymbol{ \phi}(\mathbf{ x}_i)\right), \] where \(h(\cdot)\) is the inverse link function, then this leads to an objective function of the form, \[ E(\mathbf{ w}) = - \sum_{i=1}^ny_i \log h\left(\mathbf{ w}^\top \boldsymbol{ \phi}(\mathbf{ x}_i)\right) - \sum_{i=1}^n(1-y_i)\log \left(1-h\left(\mathbf{ w}^\top \boldsymbol{ \phi}(\mathbf{ x}_i)\right)\right). \]

Negative Log Likelihood

import numpy as np

def objective(h, y):
    "Computes the objective function."
    labs = np.asarray(y, dtype=float).flatten()
    posind = np.where(labs==1)
    negind = np.where(labs==0)
    return -np.log(h[posind, :]).sum() - np.log(1-h[negind, :]).sum()

As normal, we would like to minimise this objective. This can be done by differentiating with respect to the parameters of our prediction function, \(\pi(\mathbf{ x};\mathbf{ w})\), for optimisation. The gradient of the likelihood with respect to \(\pi(\mathbf{ x};\mathbf{ w})\) is of the form, \[ \frac{\text{d}E(\mathbf{ w})}{\text{d}\mathbf{ w}} = -\sum_{i=1}^n \frac{y_i}{h\left(\mathbf{ w}^\top \boldsymbol{ \phi}(\mathbf{ x})\right)}\frac{\text{d}h(f_i)}{\text{d}f_i} \boldsymbol{ \phi}(\mathbf{ x}_i) + \sum_{i=1}^n \frac{1-y_i}{1-h\left(\mathbf{ w}^\top \boldsymbol{ \phi}(\mathbf{ x})\right)}\frac{\text{d}h(f_i)}{\text{d}f_i} \boldsymbol{ \phi}(\mathbf{ x}_i) \] where we used the chain rule to develop the derivative in terms of \(\frac{\text{d}h(f_i)}{\text{d}f_i}\), which is the gradient of the inverse link function (in our case the gradient of the sigmoid function).

So the objective function now depends on the gradient of the inverse link function, as well as the likelihood depends on the gradient of the inverse link function, as well as the gradient of the log likelihood, and naturally the gradient of the argument of the inverse link function with respect to the parameters, which is simply \(\boldsymbol{ \phi}(\mathbf{ x}_i)\).

so the full gradient can be written down as \[ \frac{\text{d}E(\mathbf{ w})}{\text{d}\mathbf{ w}} = -\sum_{i=1}^n y_i\left(1-h\left(\mathbf{ w}^\top \boldsymbol{ \phi}(\mathbf{ x})\right)\right) \boldsymbol{ \phi}(\mathbf{ x}_i) + \sum_{i=1}^n (1-y_i)\left(h\left(\mathbf{ w}^\top \boldsymbol{ \phi}(\mathbf{ x})\right)\right) \boldsymbol{ \phi}(\mathbf{ x}_i). \]

import numpy as np

def gradient(h, Phi, y):
    "Generates the gradient of the parameter vector."
    labs = np.asarray(y, dtype=float).flatten()
    posind = np.where(labs==1)
    dw = -(Phi[posind]*(1-h[posind])).sum(0)
    negind = np.where(labs==0 )
    dw += (Phi[negind]*h[negind]).sum(0)
    return dw[:, None]

Optimisation of the Function

Reorganising the gradient to find a stationary point of the function with respect to the parameters \(\mathbf{ w}\) turns out to be impossible. Optimisation has to proceed by numerical methods. Options include the multidimensional variant of Newton’s method or gradient based optimisation methods like we used for optimising matrix factorisation for the movie recommender system. We recall from matrix factorisation that, for large data, stochastic gradient descent or the Robbins Munro (Robbins and Monro, 1951) optimisation procedure worked best for function minimisation.

Multiplying everything out leads to \[ \begin{aligned} \frac{\text{d}E(\mathbf{ w})}{\text{d}\mathbf{ w}} = & -\sum_{i=1}^n y_i- h\left(\mathbf{ w}^\top \boldsymbol{ \phi}(\mathbf{ x})\boldsymbol{ \phi}(\mathbf{ x}_i). \]

Toy Data

We’ll consider a toy data set and a decision boundary that separates red crosses from green circles.

import numpy as np

np.random.seed(seed=1000001)
x_plus = np.random.normal(loc=1.3, size=(30, 2))
x_minus = np.random.normal(loc=-1.3, size=(30, 2))

Figure: Red crosses and green circles are sampled from two separate Gaussian distributions with 30 examples of each.

Now from the toy data we create design matrices with a leading column of ones (an Eins column)

import numpy as np

phi_plus = np.hstack([np.ones((x_plus.shape[0], 1)), x_plus])
phi_minus = np.hstack([np.ones((x_minus.shape[0], 1)), x_minus])

Logistic Regression vs Perceptron

We already looked at the Perceptron, where the prediction function was given by \[ f(\mathbf{ w}, \mathbf{ x}_i) = \text{sign}(\boldsymbol{ \phi}_i^\top \mathbf{ w}) \] and the sign of the output gave us the class, where we had a positive and negative class.

In logistic regression, the prediction function gives us the probability of positive class, \[ f(\mathbf{ w}, \mathbf{ x}) = \pi_i = h(\boldsymbol{ \phi}_i^\top \mathbf{ w}) \] so the two are closely related. We can think of the sigmoid as providing a “soft decision” whereas the sign provides a hard decision.

Let’s make a more detailed study by considering a stochastic gradient descent algorithm for the logistic regression of the negative log likelihood. We’ll compare that update to the Perceptron update.

We can think of the Perceptron update as randomly sampling a data point, \(i\), checking its prediction. If the predicted class doesn’t match the true class, \(y_i\), then we update the weights by subtracting \(\boldsymbol{ \phi}_i\) if the prediction is positive, and adding \(\boldsymbol{ \phi}_i\) if the prediction is negative. Using \(y_i\in\{0,1\}\) to match logistic regression, a compact update is \[ \mathbf{ w}_\text{new} \leftarrow \mathbf{ w}_\text{old} - \eta(H(\boldsymbol{ \phi}_i^\top \mathbf{ w}) (1-y_i) \boldsymbol{ \phi}_i - (1-H(\boldsymbol{ \phi}_i^\top \mathbf{ w})) y_i \boldsymbol{ \phi}_i \]

The gradient of the negative log-likelihood of logistic regression is \[ \frac{\text{d}E(\mathbf{ w})}{\text{d}\mathbf{ w}} = -\sum_{i=1}^n y_i\left(1-h\left(\mathbf{ w}^\top \boldsymbol{ \phi}_i\right)\right) \boldsymbol{ \phi}_i + \sum_{i=1}^n (1-y_i)\left(h\left(\mathbf{ w}^\top \boldsymbol{ \phi}_i\right)\right) \boldsymbol{ \phi}_i. \] so the gradient with respect to one point is \[ \frac{\text{d}E_i(\mathbf{ w})}{\text{d}\mathbf{ w}}=y_i\left(1-h\left(\mathbf{ w}^\top \boldsymbol{ \phi}_i\right)\right) \boldsymbol{ \phi}_i + (1-y_i)\left(h\left(\mathbf{ w}^\top \boldsymbol{ \phi}_i\right)\right) \boldsymbol{ \phi}_i. \] and the stochastic gradient update for logistic regression (with mini-batch size set to 1) is \[ \mathbf{ w}_\text{new} \leftarrow \mathbf{ w}_\text{old} - \eta ((1-y_i)\left(h\left(\mathbf{ w}^\top \boldsymbol{ \phi}_i\right)\right) - y_i\left(1-h\left(\mathbf{ w}^\top \boldsymbol{ \phi}_i\right)\right) \boldsymbol{ \phi}_i) \] The difference between the two is that for the perceptron we are using the Heaviside function, \(H(\cdot)\), whereas for logistic regression we’re using the sigmoid, \(h(\cdot)\), which is like a soft version of the Heaviside function.

Because \(\pi(\boldsymbol{ \phi}_i)=h(\boldsymbol{ \phi}_i)\), when \(h(\boldsymbol{ \phi}_i)>0.5\) we classify as the positive class, otherwise we classify as the negative class. So the decision boundary is just like the peceptron. The vector \(\mathbf{ w}\) gives the normal vector for the decision boundary.

In two dimensions, in the linear basis, the prediction function is \[ h\left(w_1 x_{i, 1} + w_2 x_{i, 2} + b\right) \] and the equation of a plane is \[ w_1 x_{i, 1} + w_2 x_{i, 2} + b = 0 \] or \[ w_1 x_{i, 1} + w_2 x_{i, 2} = -b. \]

We can mirror the way we implemented the Perceptron by selecting a point, \(i\), at random and setting the logistic regression weights to that point, \(\mathbf{ w}= \boldsymbol{ \phi}_i\), if it is in the positive class, and setting to \(\mathbf{ w}= -\boldsymbol{ \phi}_i\) if it is in the negatvie class. That guarantees that the selected point will be correctly classified.

def init_logistic_regression(phi_plus, phi_minus, seed=1000001):
    """
    Initialise the perceptron algorithm with random weights and bias.
    
    The perceptron is a simple binary classifier that learns a linear decision boundary.
    This function initialises the weight vector w and bias b by randomly selecting
    a point from either the positive or negative class and setting the normal vector
    accordingly.
    
    Mathematical formulation:
    The perceptron decision function is f(x) = w^T φ, where:
    - w is the weight vector (normal to the decision boundary)
    - φ is the design matrix vector
    
    :param phi_plus: Positive class data points, shape (n_plus, n_features)
    :type phi_plus: numpy.ndarray
    :param phi_minus: Negative class data points, shape (n_minus, n_features)
    :type phi_minus: numpy.ndarray
    :param seed: Random seed for reproducible initialisation
    :type seed: int, optional
    :returns: Initial weight vector, shape (n_features,)
    :rtype: numpy.ndarray
    :returns: Initial bias term
    :rtype: float
    :returns: The randomly selected point used for initialisation
    :rtype: numpy.ndarray
    
    Examples:
        >>> phi_plus = np.array([[1, 1, 2], [1, 2, 3], [1, 3, 4]])
        >>> phi_minus = np.array([[1, 0, 0], [1, 1, 0], [1, 0, 1]])
        >>> w, phi_select = init_logistic_regression(phi_plus, phi_minus)
        >>> print(f"Weight vector: {w}")
    """
    np.random.seed(seed=seed)
    # flip a coin (i.e. generate a random number and check if it is greater than 0.5)
    plus_portion = phi_plus.shape[0]/(phi_plus.shape[0] + phi_minus.shape[0])
    choose_plus = np.random.rand(1)<plus_portion
    if choose_plus:
        # generate a random point from the positives
        index = np.random.randint(0, phi_plus.shape[0])
        phi_select = phi_plus[index, :]
        w = phi_plus[index, :].astype(float)  # set the normal vector to plus that point
    else:
        # generate a random point from the negatives
        index = np.random.randint(0, phi_minus.shape[0])
        phi_select = phi_minus[index, :]
        w = -phi_minus[index, :].astype(float)  # set the normal vector to minus that point.
    return w, phi_select

Learning then proceeds

def logistic(x):
    """
    Compute the logistic function.
    """
    return 1/(1+np.exp(x))
    
def update_logistic_regression(w, phi_plus, phi_minus, learn_rate):
    """
    Update the logistic regression weights and bias using stochastic gradient descent.
    
    This function implements one step of the perceptron learning algorithm.
    It randomly selects a training point and updates the weights if the point
    is misclassified.
    
    Mathematical formulation:
    The perceptron update rule is:
    - If y_i = +1 and w^T φ_i ≤ 0: w ← w + η    h(w^Tφ_i) φ_i
    - If y_i = -1 and w^T φ_i > 0: w ← w - η (1-h(w^Tφ_i))φ_i
    
    where η is the learning rate.
    
    :param w: Current weight vector, shape (n_features,)
    :type w: numpy.ndarray
    :param phi_plus: Positive class design matrix, shape (n_plus, n_features)
    :type phi_plus: numpy.ndarray
    :param phi_minus: Negative class design matrix, shape (n_minus, n_features)
    :type phi_minus: numpy.ndarray
    :param learn_rate: Learning rate (step size) for weight updates
    :type learn_rate: float
    :returns: Updated weight vector
    :rtype: numpy.ndarray
    :returns: Updated bias term
    :rtype: float
    :returns: The randomly selected point used for the update
    :rtype: numpy.ndarray
    :returns: True if weights were updated, False otherwise
    :rtype: bool
    
    Examples:
        >>> w = np.array([0.1 0.5, -0.3])
        >>> phi_plus = np.array([[1, 1, 2], [1, 2, 3]])
        >>> phi_minus = np.array([[1, 0, 0], [1, 1, 0]])
        >>> w_new, phi_select, updated = update_perceptron(w, phi_plus, phi_minus, 0.1)
    """
    # select a point at random from the data
    plus_portion = phi_plus.shape[0]/(phi_plus.shape[0] + phi_minus.shape[0])
    choose_plus = np.random.rand(1)<plus_portion
    updated=False
    if choose_plus:
        # choose a point from the positive data
        index = np.random.randint(phi_plus.shape[0])
        phi_select = phi_plus[index, :]
        a = np.dot(w, phi_select)
        if np.dot(w, phi_select) <= 0.:
            # point is currently incorrectly classified
            w += learn_rate*logistic(a)*phi_select
            updated=True
    else:
        # choose a point from the negative data
        index = np.random.randint(phi_minus.shape[0])
        phi_select = phi_minus[index, :]
        a = np.dot(w, phi_select)
        if a > 0.:
            # point is currently incorrectly classified
            w -= learn_rate*(1-logistic(a))*phi_select
    return w, phi_select

Figure: The logistic-regression decision boundary.

Nigeria NMIS Data

As an example data set we will use Nigerian Millennium Development Goals Information System Health Facility (The Office of the Senior Special Assistant to the President on the Millennium Development Goals (OSSAP-MDGs) and Columbia University, 2014). It can be found here https://energydata.info/dataset/nigeria-nmis-education-facility-data-2014.

Taking from the information on the site,

The Nigeria MDG (Millennium Development Goals) Information System – NMIS health facility data is collected by the Office of the Senior Special Assistant to the President on the Millennium Development Goals (OSSAP-MDGs) in partner with the Sustainable Engineering Lab at Columbia University. A rigorous, geo-referenced baseline facility inventory across Nigeria is created spanning from 2009 to 2011 with an additional survey effort to increase coverage in 2014, to build Nigeria’s first nation-wide inventory of health facility. The database includes 34,139 health facilities info in Nigeria.

The goal of this database is to make the data collected available to planners, government officials, and the public, to be used to make strategic decisions for planning relevant interventions.

For data inquiry, please contact Ms. Funlola Osinupebi, Performance Monitoring & Communications, Advisory Power Team, Office of the Vice President at funlola.osinupebi@aptovp.org

To learn more, please visit http://csd.columbia.edu/2014/03/10/the-nigeria-mdg-information-system-nmis-takes-open-data-further/

Suggested citation: Nigeria NMIS facility database (2014), the Office of the Senior Special Assistant to the President on the Millennium Development Goals (OSSAP-MDGs) & Columbia University

For ease of use we’ve packaged this data set in the pods library

data = pods.datasets.nigeria_nmis()['Y']
data.head()

Alternatively, you can access the data directly with the following commands.

import urllib.request
urllib.request.urlretrieve('https://energydata.info/dataset/f85d1796-e7f2-4630-be84-79420174e3bd/resource/6e640a13-cab4-457b-b9e6-0336051bac27/download/healthmopupandbaselinenmisfacility.csv', 'healthmopupandbaselinenmisfacility.csv')

import pandas as pd
data = pd.read_csv('healthmopupandbaselinenmisfacility.csv')

Once it is loaded in the data can be summarized using the describe method in pandas.

data.describe()

We can also find out the dimensions of the dataset using the shape property.

data.shape

Dataframes have different functions that you can use to explore and understand your data. In python and the Jupyter notebook it is possible to see a list of all possible functions and attributes by typing the name of the object followed by .<Tab> for example in the above case if we type data.<Tab> it show the columns available (these are attributes in pandas dataframes) such as num_nurses_fulltime, and also functions, such as .describe().

For functions we can also see the documentation about the function by following the name with a question mark. This will open a box with documentation at the bottom which can be closed with the x button.

data.describe?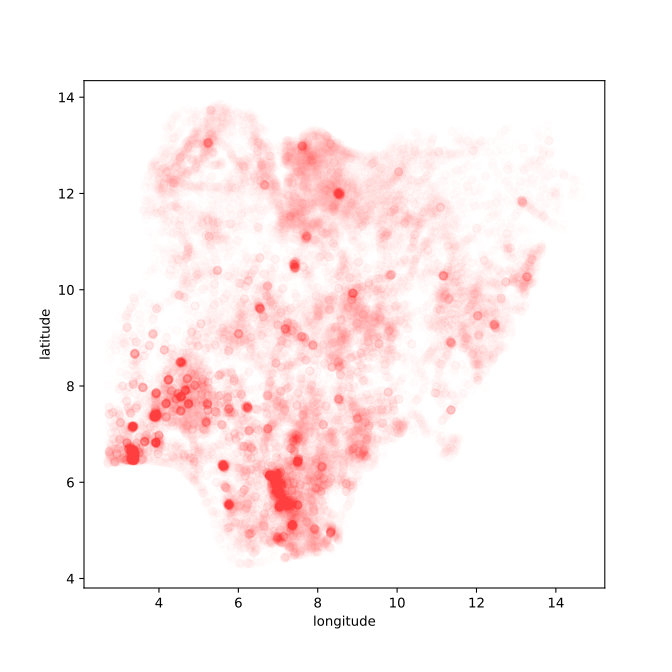

Figure: Location of the over thirty-four thousand health facilities registered in the NMIS data across Nigeria. Each facility plotted according to its latitude and longitude.

Nigeria NMIS Data Classification

Our aim will be to predict whether a center has maternal health delivery services given the attributes in the data. We will predict of the number of nurses, the number of doctors, location etc.

Now we will convert this data into a form which we can use as inputs X, and labels y.

import pandas as pd
import numpy as np

data = data[~pd.isnull(data['maternal_health_delivery_services'])]
data = data.dropna() # Remove entries with missing values
X = data[['emergency_transport',
          'num_chews_fulltime', 
          'phcn_electricity',
          'child_health_measles_immun_calc',
          'num_nurses_fulltime',
          'num_doctors_fulltime', 
          'improved_water_supply', 
          'improved_sanitation',
          'antenatal_care_yn', 
          'family_planning_yn',
          'malaria_treatment_artemisinin', 
          'latitude', 
          'longitude']].copy()
y = data['maternal_health_delivery_services']==True  # set label to be whether there's a maternal health delivery service

# Create series of health center types with the relevant index
s = data['facility_type_display'].apply(pd.Series).stack()
s.index = s.index.droplevel(-1) # to line up with df's index

# Extract from the series the unique list of types.
types = s.unique()

# For each type extract the indices where it is present and add a column to X
type_names = []
for htype in types:
    index = s[s==htype].index.tolist()
    type_col=htype.replace(' ', '_').replace('/','-').lower()
    type_names.append(type_col)
    X.loc[:, type_col] = 0.0 
    X.loc[index, type_col] = 1.0

This has given us a new data frame X which contains the different facility types in different columns.

X.describe()

Batch Gradient Descent

We will need to define some initial random values for our vector and then minimize the objective by descending the gradient.

# Separate train and test
indices = np.random.permutation(X.shape[0])
num_train = int(np.ceil(X.shape[0]/2))
train_indices = indices[:num_train]
test_indices = indices[num_train:]
X_train = X.iloc[train_indices]
y_train = y.iloc[train_indices]==True
X_test = X.iloc[test_indices]
y_test = y.iloc[test_indices]==True

import numpy as np

# gradient descent algorithm
w_vals = np.random.normal(size=(X.shape[1]+1, 1), scale = 0.001)
# Convert weights to a pandas DataFrame with column names
if type(X_train) is pd.DataFrame:
    w = pd.DataFrame(data=w_vals, 
                     index=['Eins'] + list(X_train.columns), 
                     columns=['weight'])

eta = 1e-9
iters = 10000
for i in range(iters):
    g, Phi = predict(w, X_train, mlai.linear)
    w -= eta*gradient(g, Phi, y_train) + 0.001*w
    if not i % 100:
        print("Iter", i, "Objective", objective(g, y_train))

Let’s look at the weights and how they relate to the inputs.

import matplotlib.pyplot as plt

# Plot a histogram of the weights
plt.figure(figsize=(10, 6))
if type(w) is pd.DataFrame:
    plt.bar(w.index, w['weight'])
else:
    plt.bar(w)
plt.xticks(rotation=90)
plt.xlabel('Features')
plt.ylabel('Weight Value')
plt.title('Histogram of Model Weights')
plt.tight_layout()
mlai.write_figure('nmis-logistic-regression-weights.svg', directory='./ml')

Exercise 1

What does the magnitude of the weight vectors tell you about the different parameters and their influence on outcome? Are the weights of roughly the same size, if not, how might you fix this?

g_test, Phi_test = predict(w, X_test, mlai.linear)
np.sum(g_test[y_test]>0.5)

Stochastic Gradient Descent

Exercise 2

Now construct a stochastic gradient descent algorithm and run it on the data. Is it faster or slower than batch gradient descent? What can you do to improve convergence speed?

%pip install statsmodels

Model Diagnostics and Linear Regression

In linear regression, we model the relationship between a continuous response variable \(y_i\) and input variables \(\mathbf{ x}_i\) through a linear function with Gaussian noise:

\[y_i = f(\mathbf{ x}_i) + \epsilon_i\]

where \(f(\mathbf{ x}_i) = \mathbf{ w}^\top\mathbf{ x}_i = \sum_{j=1}^D w_jx_{i,j}\) and \(\epsilon_i \sim \mathscr{N}\left(0,\sigma^2\right)\)

This gives us a probabilistic model:

\[p(y_i|\mathbf{ x}_i) = \mathscr{N}\left(y_i|\mathbf{ w}^\top\mathbf{ x}_i,\sigma^2\right)\]

The key components are:

• \(y_i\) is the target/response variable we want to predict
• \(\mathbf{ x}_i\) contains the input features/explanatory variables
  
• \(\mathbf{ w}\) contains the parameters/coefficients we learn
• \(\epsilon_i\) represents random Gaussian noise with variance \(\sigma^2\)

For the full dataset, we can write this in matrix form:

\[\mathbf{ y}= \mathbf{X}\mathbf{ w}+ \boldsymbol{ \epsilon}\]

where \(\mathbf{ y}= [y_1,\ldots,y_N]^\top\), \(\mathbf{X}\) contains the input vectors as rows, and \(\boldsymbol{ \epsilon}\sim \mathscr{N}\left(\mathbf{0},\sigma^2\mathbf{I}\right)\).

The expected value of our prediction is:

\[\mathbb{E}[y_i|\mathbf{ x}_i] = \mathbf{ w}^\top\mathbf{ x}_i\]

This linear model forms the foundation for generalized linear models like logistic regression, where we’ll adapt the model for classification by transforming the output through a non-linear function.

import statsmodels.api as sm
import pods

# Demo of linear regression using python statsmodels.
data = pods.datasets.olympic_marathon_men()
xlim = (1876,2044)
x = data['X']
y = data['Y']

The statsmodels package makes it easy to add the constant term to the matrix.

# Add constant term to design matrix
print(x.shape)
x = sm.add_constant(x)
print(x.shape)

model = sm.OLS(y, x)

Using statsmodels we don’t need to implement the QR decomposition directly we can simply fit the model.

results = model.fit()

The model results also contain a lot more than just the regression weights. Various diagnostic statistics are also computed including checks on the residuals (i.e. \(y_i - f_i\)) which should be Gaussian (or normal) distributed.

We can show obtain our predictions, \(f\) from the model as follows.

f = results.predict(x)

And plot them against the actual data.

Figure: Plot of the statsmodels fit to the olympic marathon data.

results.summary()

The summary helps us evaluate our model fit and identify potential areas for improvement. Since we’re working with one-dimensional data (year vs time), we can visualise everything easily to complement these statistical measures.

The model fit statistics show a moderately strong fit, with an R-squared of 0.730 indicating that our model explains 73.0% of the variance in the data. The adjusted R-squared of 0.721 confirms this isn’t just due to overfitting (which is unsurprising given we are only fitting a linear model). The very low F-statistic p-value (1.85e-09) confirms the model’s overall significance.

The AIC (11.33) and BIC (14.13) information criteria values are used to compare the model against alternatives we might try.

Looking at the model parameters, we see a coefficient of -0.0116 for our predictor, with a small standard error (0.001). The \(t\)-statistic of -8.710 and p-value of less than 0.001 indicate this effect is highly significant. The 95% confidence interval [-0.014, -0.009] gives us good confidence in our estimate. The negative coefficient confirms the expected downward trend in marathon times over the years.

Figure: The histogram of the residuals of the fit to the Olympic Marathon data.

We can see in the histogram that the residuals are not Gaussian (normal) distributed. Looking at the diagnostics we see the same challenges. The histogram doesn’t show us the autocorrelation, that comes from the Durbin-Watson statistic.

1. The Durbin-Watson statistic (0.981) indicates positive autocorrelation in the residuals. This suggests we might want to

   • Consider time series modeling approaches
   • Add polynomial terms to capture non-linear trends
   • Investigate if there are distinct “eras” in marathon times

2. The Jarque-Bera test (\(p\)-value 8.32e-14) tells us our residuals aren’t normally distributed. The skew (1.947) and kurtosis (8.746) values show the distribution is strongly right-skewed with very heavy tails. This is due to the outlier in 1904. We could deal with this through transformation of the response variable, robust regression or by dropping the outlier.

3. The large condition number (9.94e+04) suggests potential numerical instability or multicollinearity issues. This is because we haven’t centred and scaled the model.

The beauty of having one-dimensional data is that we can plot everything to visually confirm these statistical findings. It allows us to visually assess the linearity assumption, identify potential outliers (such as the 1904 point) and spot any systematic patterns in the residuals.

This visual inspection, combined with our statistical diagnostics, will guide our next steps in improving the model.

Figure: Linear regression fit to Olympic marathon men’s times using statsmodels.

Looking at our plot and model diagnostics, we can now better understand the large condition number (1.08e+05) in our results. This high value likely stems from using raw year values (e.g., 1896, 1900, etc.) as our predictor variable. Such large numbers can lead to numerical instability in the computations.

To address this, we will look at centering the years around their mean and scaling the years to a smaller range.

Looking at the plot we can see more about our our data. The 1904 St. Louis Olympics appears as a clear outlier, contributing to the non-normal residuals (Jarque-Bera p=0.00432) and right-skewed distribution (skew=1.385).

There are also regimes in the data, such as the rapid improvement in times pre-WWI, the disruption and variation during the war years, the more steady, consistent progress post-WWII. These regime changes help explain the strong positive autocorrelation (Durbin-Watson=0.242) in our residuals.

This suggests we could improve the model by adding additional features such as polynomial terms to capture non-linear trends, indicator variables for different time periods and interaction terms between features. We could also consider variables accounting for external factors like temperature or course conditions.

To incorporate multiple features into our model, we need a systematic way to organize this additional information. This brings us back to the concept of the design matrix.

Design Matrix

The design matrix, often denoted as \(\boldsymbol{ \Phi}\), is a key component of a statistical model. It organizes our feature data in a structured way that facilitates model fitting and analysis. Each row of the design matrix represents a single observation or data point, while each column represents a different feature or predictor variable.

For \(n\) observations and \(p\) features, the design matrix takes the form:

\[\boldsymbol{ \Phi}= \begin{bmatrix} \phi_{11} & \phi_{12} & \cdots & \phi_{1p} \\ \phi_{21} & \phi_{22} & \cdots & \phi_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ \phi_{n1} & \phi_{n2} & \cdots & \phi_{np} \end{bmatrix}\]

For example, if we’re predicting house prices, each row might represent a different house, with columns for features like: square footage, number of bedrooms, yyear built, plot size.

The design matrix provides a compact way to represent all our feature data and is used directly in model fitting. When we write our linear model as \(\mathbf{ y}= \boldsymbol{ \Phi}\mathbf{ w}+ \boldsymbol{ \epsilon}\), the design matrix \(\boldsymbol{ \Phi}\) is multiplied by our parameter vector \(\mathbf{ w}\) to generate predictions.

import statsmodels.api as sm
import pods
import numpy as np

# Demo of additional features with interactions regression usying python statsmodels.
data = pods.datasets.olympic_marathon_men()
x = data['X']
y = data['Y']
xlim = (1876,2044)

Now we process our input data to create the design matrix.

def marathon_design_matrix(x, product_terms=True):
    """This function augments the input matrix with indicator variables that state the year."""
    
    # Scale the year to avoid numerical issues
    x_scaled = (x - 1900) / 100  # Center around 1900 and scale to century units
    Phi = x_scaled

    # Add to design matrix indicator variable for 1914-1945
    Phi = np.hstack([Phi, ((x[:, 0] >= 1914) & (x[:, 0] <= 1945)).astype(np.float64)[:, np.newaxis]])

    # Add to design matrix indicator variable for post-1945
    Phi = np.hstack([Phi, (x[:, 0] > 1945).astype(np.float64)[:, np.newaxis]])
    if product_terms:
        # Add product terms that multiply the scaled year and the indicator variables.
        Phi = np.hstack([Phi, x_scaled[:, 0:1] * Phi[:, 1:2], x_scaled[:, 0:1] * Phi[:, 2:3]])
    Phi = sm.add_constant(Phi)
    return Phi

# Create the model
Phi = marathon_design_matrix(x)
model = sm.OLS(y, Phi)

Now we can fit the model.

# Do the linear fit
results = model.fit()

Figure: Plot of the fit obtained when we include indicator variables that identify the pre-1914, across war, and post-war eras.

Let’s check the summary of the results.

results.summary()

Using indicator variables for historical periods (and without relying on quadratic terms), the model shows a strong improvement over the simpler linear model, with an R-squared of 0.877 and an adjusted R-squared of 0.851. This indicates that about 87% of the variance in marathon times is explained by our model. The overall model significance is high (F-statistic \(p=3.70\times 10^{-10}\)), and the information criteria are AIC \(=-4.164\), BIC \(=4.244\).

Key parameter estimates (with 95% confidence intervals) are:

• Intercept (const): \(4.5876\) (SE \(0.113\)), \(t=40.533\), \(p=0.000\), CI \([4.354, 4.821]\)
• \(x_1\) (base time trend): \(-3.6127\) (SE \(1.634\)), \(t=-2.211\), \(p=0.037\), CI \([-6.984, -0.241]\)
• \(x_2\) (war period indicator): \(-0.7523\) (SE \(0.480\)), \(t=-1.567\), \(p=0.130\), CI \([-1.743, 0.239]\)
• \(x_3\) (post war indicator): \(-0.9399\) (SE \(0.211\)), \(t=-4.449\), \(p=0.000\), CI \([-1.376, -0.504]\)
• \(x_4\) (wartime time trend): \(2.8799\) (SE \(2.310\)), \(t=1.247\), \(p=0.225\), CI \([-1.888, 7.648]\)
• \(x_5\) (post war time trend): \(3.0493\) (SE \(1.646\)), \(t=1.853\), \(p=0.076\), CI \([-0.348, 6.446]\)

These results suggest a strong negative time trend and statistically significant effects for some period indicators, with others being suggestive but not conclusive.

However, there are some concerns:

1. The Jarque–Bera test (\(p=1.34\times 10^{-24}\)) indicates non-normal residuals. Skewness is \(2.393\) and kurtosis is \(11.065\).
2. The Durbin–Watson statistic is \(2.101\), suggesting little residual autocorrelation.
3. The condition number is \(127\), indicating the design is reasonably well conditioned relative to polynomial/interaction-augmented alternatives.

The indicator-variable model captures key regime differences and substantially improves fit over the baseline linear model. One side-effect of using abrupt indicator boundaries is that the fitted curve is discontinuous at regime change years. This can create edge effects where adjacent observations on either side of a boundary receive different offsets even if they are close in time.

If continuity is needed we could consider

• Replacing hard indicators with smooth transition functions (e.g., logistic ramps centered on boundary years)
• Adding interaction terms with polynomial or spline bases to allow the trend to bend smoothly through transitions
• Using piecewise-linear or spline regression with continuity (and optionally slope) constraints at knots
• Hierarchical/regularized models that shrink jump sizes toward zero unless strongly supported by data

These approaches preserve the idea of regime structure while avoiding artificial jumps at the boundaries.

Fitting with statsmodels

Fitting the Model

import statsmodels.api as sm
import numpy as np
import pandas as pd
from sklearn.datasets import make_classification

# Demo of logistic regression using python statsmodels.
# Create a synthetic binary classification dataset
X, y = make_classification(n_samples=200, n_features=2, n_redundant=0, 
                         n_informative=2, n_clusters_per_class=1, 
                         random_state=42)

# Convert to DataFrame for easier handling
df = pd.DataFrame(X, columns=['feature1', 'feature2'])
df['target'] = y

# Split into train and test sets
indices = np.random.permutation(df.shape[0])
num_train = int(np.ceil(df.shape[0]/2))
train_indices = indices[:num_train]
test_indices = indices[num_train:]

X_train = df[['feature1', 'feature2']].iloc[train_indices]
y_train = df['target'].iloc[train_indices]
X_test = df[['feature1', 'feature2']].iloc[test_indices]
y_test = df['target'].iloc[test_indices]

# Add constant term to design matrix
X_train_sm = sm.add_constant(X_train)
X_test_sm = sm.add_constant(X_test)

# Fit logistic regression model
model = sm.Logit(y_train, X_train_sm)
results = model.fit()
results.summary()

Model Fit Statistics

The statsmodels summary for logistic regression provides several diagnostic measures that help us evaluate our classification model’s performance and identify potential areas for improvement.

Model Fit Statistics: The logistic regression model doesn’t have a traditional R-squared since we’re dealing with binary outcomes rather than continuous responses. Instead, we use pseudo R-squared measures:

• McFadden’s R-squared: Compares the log-likelihood of our model to a null model with only an intercept. Values between 0.2-0.4 indicate excellent fit.
• Log-Likelihood Ratio (LLR) test: Tests whether our model is significantly better than the null model. A low p-value indicates our predictors significantly improve the model.
• AIC/BIC: Help compare different model specifications. Lower values indicate better models when comparing alternatives.

Parameter Interpretation: The coefficients in logistic regression represent changes in log-odds: - A positive coefficient means the feature increases the odds of the positive class - A negative coefficient means the feature decreases the odds of the positive class
- The magnitude indicates the strength of the effect - To get odds ratios, we exponentiate the coefficients: \(\exp(\beta_j)\)

For example, if a coefficient is 0.693, then \(\exp(0.693) = 2.0\), meaning a one-unit increase in that feature doubles the odds of the positive outcome.

Diagnostic Considerations: Unlike linear regression, logistic regression has different diagnostic concerns:

1. Multicollinearity: Check condition numbers and correlation matrices, just like in linear regression
2. Outliers and Influential Points: Use deviance residuals and leverage measures to identify problematic observations
3. Model Adequacy: Hosmer-Lemeshow test checks if predicted probabilities match observed frequencies
4. Separation: Perfect or quasi-perfect separation can cause convergence issues and inflated standard errors

Classification Performance: Beyond the statistical diagnostics, we should evaluate practical classification performance: - Confusion Matrix: Shows true vs predicted classifications - Accuracy: Overall percentage of correct predictions
- Precision/Recall: Important when classes are imbalanced - ROC/AUC: Measures discrimination ability across different thresholds

Predictions of the Model

# Make predictions on test set
y_pred_proba = results.predict(X_test_sm)
y_pred = (y_pred_proba > 0.5).astype(int)

# Calculate classification metrics
from sklearn.metrics import accuracy_score, confusion_matrix, classification_report
accuracy = accuracy_score(y_test, y_pred)
conf_matrix = confusion_matrix(y_test, y_pred)

print(f"Test Accuracy: {accuracy:.3f}")
print(f"Confusion Matrix:\n{conf_matrix}")
print(f"\nClassification Report:\n{classification_report(y_test, y_pred)}")

Figure: Plot of the logistic regression fit made by statsmodels.

Looking at our classification results, we can evaluate several aspects of model performance:

Decision Boundary Analysis: The visualization shows how our logistic regression model creates a linear decision boundary in the feature space. The dashed black line represents the 0.5 probability threshold where the model switches between predicting class 0 and class 1. The colored contours show the predicted probability landscape - areas closer to red have higher probability of being class 1, while areas closer to blue have higher probability of being class 0.

Model Performance: From the classification metrics, we can assess: - Accuracy: Overall percentage of correct predictions on the test set - Confusion Matrix: Shows the breakdown of true positives, false positives, true negatives, and false negatives - Precision and Recall: Important when we care about specific types of errors (e.g., medical diagnosis)

Potential Issues to Monitor: 1. Feature Scaling: If features have very different scales, consider standardization 2. Linear Separability: Our model assumes a linear decision boundary - if classes aren’t linearly separable, consider polynomial features or non-linear methods 3. Class Imbalance: If one class dominates, consider resampling techniques or adjusting the decision threshold 4. Overfitting: Monitor performance on validation data, especially with many features

Figure: Logistic regression classification results showing training data and decision boundary with probability contours using statsmodels.

The classification visualization reveals several important aspects of our logistic regression model:

Linear Decision Boundary: The model creates a straight-line decision boundary (shown as the dashed line at 0.5 probability). This linear separator works well when classes are roughly linearly separable, but may struggle with more complex class distributions.

Probability Gradients: The colored contours show how predicted probabilities change smoothly across the feature space. Points far from the decision boundary have probabilities close to 0 or 1 (high confidence), while points near the boundary have probabilities around 0.5 (uncertain predictions).

Model Extensions: For more complex classification problems, we can enhance the basic logistic regression model: - Polynomial Features: Add \(x_1^2\), \(x_2^2\), \(x_1 x_2\) terms for non-linear decision boundaries - Feature Interactions: Include products of features to capture synergistic effects - Regularization: Add L1 (Lasso) or L2 (Ridge) penalties to prevent overfitting - Feature Engineering: Transform or combine features to better capture relationships

To incorporate multiple features and transformations into our model, we need a systematic way to organize this information through the design matrix.

Categorical (Multinomial) Regression

This is the multi-class analogue of logistic regression. Instead of a single Bernoulli outcome, we model a \(K\)-way categorical outcome using a softmax link over class-specific linear scores.

Soft Arg Max (Softmax) Function

Given class scores \(f_k(\mathbf{ x})=\mathbf{ w}_k^\top\boldsymbol{ \phi}(\mathbf{ x})\), the softmax maps scores to probabilities: \(\pi_k = \frac{\exp(f_k)}{\sum_{j=1}^K \exp(f_j)}\).

Prediction Function

For class \(k\in\{1,\dots,K\}\), define a linear score \(f_k(\mathbf{ x})=\mathbf{ w}_k^\top\boldsymbol{ \phi}(\mathbf{ x})\). The predictive probabilities are given by the softmax: \[ \pi_k(\mathbf{ x}) = \frac{\exp\left(f_k(\mathbf{ x})\right)}{\sum_{j=1}^K \exp\left(f_j(\mathbf{ x})\right)}. \]

Maximum Likelihood

With one-hot targets \(\mathbf{ y}_i\in\{0,1\}^K\) and softmax probabilities \(\pi_{ik}\), the (negative) log-likelihood is \[ E(\{\mathbf{ w}_k\}) = -\sum_{i=1}^n\sum_{k=1}^K y_{ik}\log \pi_{ik}. \]

Other GLMs

We’ve introduced the formalism for generalised linear models. Have a think about how you might model count data using the Poisson distribution and a log link function for the rate, \(\lambda(\mathbf{ x})\). If you want a data set you can try the pods.datasets.google_trends() for some count data.

Other GLMs

We’ve introduced the formalism for generalised linear models. Have a think about how you might model count data using the Poisson distribution and a log link function for the rate, \(\lambda(\mathbf{ x})\). If you want a data set you can try the pods.datasets.google_trends() for some count data.

Poisson Distribution

Figure: The Poisson distribution.

Poisson Regression

Poisson regression is a type of generalized linear model (GLM) used when modeling count data. It assumes the response variable follows a Poisson distribution and uses a logarithmic link function to relate the mean of the response to the linear predictor.

In this model, we make the rate parameter λ a function of covariates (like space or time). The logarithm of the rate is modeled as a linear combination of the input features:

\[\log \lambda(\mathbf{ x}, t) = \mathbf{ w}_x^\top \boldsymbol{ \phi}_x(\mathbf{ x}) + \mathbf{ w}_t^\top \boldsymbol{ \phi}_t(t)\]

where: - \(\mathbf{ w}_x\) and \(\mathbf{ w}_t\) are parameter vectors - \(\boldsymbol{ \phi}_x(\mathbf{ x})\) and \(\boldsymbol{ \phi}_t(t)\) are basis functions for space and time respectively

This formulation is known as a log-linear or log-additive model because we’re adding terms in the log space. The logarithm serves as our link function, connecting the linear predictor to the response variable’s mean.

An important characteristic of this model that practitioners should be aware of is that while we add terms in the log space, the model becomes multiplicative when we transform back to the original space. This happens because:

1. We start with the log-additive form: \(\log \lambda(\mathbf{ x}, t) = f_x(\mathbf{ x}) + f_t(t)\)

2. When we exponentiate both sides to get back to λ, the addition in log space becomes multiplication: \[\lambda(\mathbf{ x}, t) = \exp(f_x(\mathbf{ x}) + f_t(t)) = \exp(f_x(\mathbf{ x}))\exp(f_t(t))\]

This multiplicative nature has important implications for interpretation. For example, if we increase one input variable, it has a multiplicative effect on the rate, not an additive one. This can lead to rapid growth in the predicted counts as input values increase.

Let’s look at another example using synthetic data to demonstrate Poisson regression without relying on external APIs.

import numpy as np
import statsmodels.api as sm

# Generate some example count data
np.random.seed(42)
n_samples = 100
x1 = np.random.uniform(0, 10, n_samples)
x2 = np.random.uniform(0, 5, n_samples)
X = np.column_stack((x1, x2))

# True relationship: y ~ Poisson(exp(1 + 0.3*x1 - 0.2*x2))
lambda_true = np.exp(1 + 0.3*x1 - 0.2*x2)
y = np.random.poisson(lambda_true)

# Fit Poisson regression
model_synthetic = sm.GLM(y, sm.add_constant(X), family=sm.families.Poisson())
result_synthetic = model_synthetic.fit()

The statsmodels library in Python provides a convenient way to fit Poisson regression models. The sm.GLM function is used to fit generalized linear models, and we specify the Poisson family to indicate that we’re modeling count data. The sm.add_constant(x) function adds a column of ones to the design matrix to account for the intercept term.

In this synthetic example, we generate count data that follows a Poisson distribution where the rate parameter \(\lambda\) depends on two predictor variables. This demonstrates how Poisson regression can model count data with multiple predictors.

Figure: Diagnostic plots for the Poisson regression model showing actual vs predicted counts and residual analysis.

The Exponential Family

An important class of distribution is known as the exponential family. These distributions can be written as \[ p(\mathbf{ y}| \boldsymbol{ \theta}) = \exp(\boldsymbol{ \theta}^\top T- A(\boldsymbol{ \theta})) h(\boldsymbol{ \theta}) \] where \(\boldsymbol{ \theta}\) is known as the , \(T(\mathbf{ y})\) is known as the and \(A\) is the the log partition function, or the and \(h(\cdot)\) is known as the base measure.

For the moment we’ll ignore the base measure as for several of the distributions we’ll considere it’s constant, so we will consider the form \[ p(\mathbf{ y}| \boldsymbol{ \theta}) = \exp(\boldsymbol{ \theta}^\top T- A(\boldsymbol{ \theta})). \] This form yields a particularly simple likelihood function \[ L(\boldsymbol{ \theta}) = \boldsymbol{ \theta}^\top T- A(\boldsymbol{ \theta}) \] and since the gradient of the cumulant generating function is the first cumulant of the sufficient statistics, the gradient of the log likelihood also has a simple form. \[ \nabla_\boldsymbol{ \theta}L(\boldsymbol{ \theta}) = T- \left\langle T\right\rangle_{p(\mathbf{ y}|\boldsymbol{ \theta})}. \] where $ denotes the expecttion under the distribution \(p(\cdot)\).

Exponential Family Regression

An important class of distribution is known as the exponential family. These distributions can be written as \[ p(\mathbf{ y}| \boldsymbol{ \theta}) = \exp(\boldsymbol{ \theta}^\top T- A(\boldsymbol{ \theta})) h(\boldsymbol{ \theta}) \] where \(\boldsymbol{ \theta}\) is known as the , \(T(\mathbf{ y})\) is known as the and \(A\) is the the log partition function, or the and \(h(\cdot)\) is known as the base measure.

For the moment we’ll ignore the base measure as for several of the distributions we’ll considere it’s constant, so we will consider the form \[ p(\mathbf{ y}| \boldsymbol{ \theta}) = \exp(\boldsymbol{ \theta}^\top T- A(\boldsymbol{ \theta})). \] This form yields a particularly simple likelihood function \[ L(\boldsymbol{ \theta}) = \boldsymbol{ \theta}^\top T- A(\boldsymbol{ \theta}) \] and since the gradient of the cumulant generating function is the first cumulant of the sufficient statistics, the gradient of the log likelihood also has a simple form. \[ \nabla_\boldsymbol{ \theta}L(\boldsymbol{ \theta}) = T- \left\langle T\right\rangle_{p(\mathbf{ y}|\boldsymbol{ \theta})}. \] where $ denotes the expecttion under the distribution \(p(\cdot)\).

This leads to a special form of generalised linear model we call the canonical form where the link function is such that the linear function is the natural parameter of the distribution. For example if we have a categorical distribution with natural parameters \(\theta_{i,j}\), the sufficient statistic is a matrix \(\mathbf{Y}\) where \(y_{i,j} = 1\) if the \(j\)th category is observed for the \(i\)th data point. Now if we give the natural parameters a linear relationship with the design matrix, \[ \boldsymbol{ \Theta}= \boldsymbol{ \Phi}\mathbf{W} \] which is equivalent to suggesting that each natural parameter is given by \[ \theta_{i,j} = \mathbf{ w}{:, j}^\top\boldsymbol{ \phi}_{i,:}. \] The link function that recovers this relation is known as the canonical link function.

{For this form the gradient of the log likelihood with respect to the model’s parameters is given by \[ \nabla_\mathbf{W}L(\mathbf{W}) = \left(T- \left\langle T\right\rangle_{p(\mathbf{ y}|\boldsymbol{ \theta})})\boldsymbol{ \Phi}. \] This very simple form covers all the examples we have presented so far. Let’s consider their exponential family form one by one. One of the easiest to start with is the Bernoulli probability.

Bernoulli as Exponential Family

The Bernoulli probability is given by \[ P(y) = \pi^y(1-\pi)^(1-y) \] where \(\pi\) is the probability of a \(y=1\) outcome. In exponential family form the natural parameter is given by \(\theta= \log \frac{\pi}{1-\pi}\) and the sufficient statistics are given by \(y\). The distribution is written as \[ P(y|\theta) = \exp(y \theta- \cumualantGeneratingFunction(\theta)) \] where \[ A(\theta) = \log(1 + \exp(\theta)). \] We can substitute back into the exponential family form to recover the original form by first recognising that \[ \pi_i = \frac{\exp(\theta)}{1+\exp(\theta)} \] which implies that \(A(\theta) = - \log (1- \pi)\). Substituting this and the form of the natural parameter back into the distribution we recover \[ P(y|\pi) = \exp\left(y\log \pi + (1-y)\log (1-\pi)\right) \] which can be rewritten as \(\pi^y(1-\pi)^(1-y)\) as required.

Categorical Distribution as Exponental Family

The categorical distribution can be seen as a generalisation of the Bernoulli to multiple outcomes. For this distribution we have \[ P(\mathbf{ y}) = \prod_{j=1}^C \pi_j^y_j \] where the \(\mathbf{ y}\) is a vector of all zeros apart from the \(k\)th element whcih is one.

The natural parameters are given by \(\theta_i = \log \pi_i\) and the sufficient statistics are just given by \(\mathbf{ y}\), \[ P(\mathbf{ y}) = \exp\left(\mathbf{ y}^\top \boldsymbol{ \theta}- A(\boldsymbol{ \theta})\right) \] where \(A(\boldsymbol{ \theta}) = \log \sum_{i=1}^C \exp(\theta_i)\).

Gaussian as Exponential Family

{The natural parameters of a univariate Gaussian with mean, \(\mu\) and variance \(\sigma^2\), \[ y \sim \mathscr{N}\left((,\mu\right), \sigma^2) \] are \(\theta_1 = \frac{\mu}{\sigma^2}\) and \(\theta_2 = -\tfrac{1}{2\sigma^2}\). This allows us to write \[ p(y | \boldsymbol{ \theta}) = \exp(\nu_1 y + \nu_2 y^2 - A(\boldsymbol{ \theta}) \] where the log partition function is \[ A(\theta_1, \theta_2) = \frac{\theta_1^2}{4\theta_2} - \frac{1}{2}\log\det{-2\theta_2} - \frac{1}{2}\log 2\pi. \]

Poisson Distribution in Exponential Family Form

The Poisson distribution is given by \[ P(y| \lambda) = \frac{\lambda^y\exp(-\lambda)}{y!} \] natural parameter of the Poisson is \(\theta= \log \lambda\). The sufficient statistic is \(y\) and in the Poisson case we cannot ignore the base measure. It is given by \(h(y) = \frac{1}{y!}\). The log partition function is \[ A(\theta) = \exp(\theta) \]

Practical Tips

{In practice feature engineering is critical to the success of a GLM. Build modular data processing pipelines that allow you to easily test different feature sets. For example, if modeling house prices, you might want to test combinations of raw features (square footage, bedrooms), derived features (price per square foot), and interaction terms (bedrooms \(\times\) bathrooms). Consider non-linear transformations of continuous variables. For instance, taking the log of price data often helps normalise distributions. Be thoughtful about encoding categorical variables. One-hot encoding isn’t always optimal, for high-cardinality categories, consider target encoding or feature hashing. Scale features appropriately: standardization or min-max scaling depending on your model assumptions. Document your feature creation process thoroughly, including the rationale for each transformation. Jupyter notebooks can be a good place to do this.

Model validation requires careful consideration. Cross-validation should match your real-world use case. For time series data, use time-based splits rather than random splits. Bootstrap sampling can help with understanding parameter uncertainty. For example, bootstrapping can show if a coefficient’s sign might flip under different samples. Hold-out test sets should be truly independent. In a customer churn model, this might mean testing on future customers rather than a random subset. Watch for data leakage, especially with time-dependent features. E.g. if predicting customer churn, using future purchase data would create leakage.

Diagnostic checks are essential for building confidence about the model reliability. Create residual plots against fitted values and each predictor. Look for systematic patterns, a U-shaped residual plot suggests missing quadratic terms. For logistic regression, plot predicted probabilities against actual outcomes in bins to check calibration. Calculate influence measures like Cook’s distance to identify outliers. In a house price model, a mansion might have outsized influence on coefficients. Check variance inflation factors (VIF) for multicollinearity. High VIF (>5-10) suggests problematic correlation between predictors.

Visualisation remains crucial throughout. Before modeling, create scatter plots, box plots, and histograms to understand your data distribution and relationships. Use pairs plots to identify correlations and potential interactions between features. Create residual diagnostic plots including Q-Q plots for normality checking. When communicating results, focus on interpretable visualizations. For instance, partial dependence plots can show how predictions change with a single feature.

Other practical considerations include starting simple and add complexity incrementally. A basic linear model often provides a good baseline. Keep track of model performance metrics across iterations to ensure changes actually improve results. Consider the computational cost of feature engineering: some transformations might not be feasible in production. Think about how features will be available in production. If a feature requires complex processing or external data, it might not be practical. For categorical variables with many levels, consider grouping rare categories. When dealing with missing data, document your imputation strategy and test its impact on model performance. When using the Access, Assess, Address approach remember that documentation of the missing values is part of Assess. Imputation can only occur in Address.

Further Reading

• Section 5.2.2 up to pg 182 of Rogers and Girolami (2011)

Thanks!

For more information on these subjects and more you might want to check the following resources.

• company: Trent AI
• book: The Atomic Human
• twitter: @lawrennd
• podcast: The Talking Machines
• newspaper: Guardian Profile Page
• blog: http://inverseprobability.com

References