Generalised Linear Models

Review

• In introduction lecture introduced log odds and probability.
• “Buy a jumper example”

Logistic Regression

• Model the log odds with a linear model.

Logistic Regression

• In regression we model probability of \(y_i |\mathbf{ x}_i\) directly
• Allows less flexibility in questions, but more flexibility in model assumptions

Log Odds

• Model the log-odds with basis functions
• Odds are ratio of probability of positive vs negative outcome

Log Odds

• Probability is between zero and one
• Odds are: \[ \frac{\pi}{1-\pi} \]

Log Odds

• Odds are between \(0\) and \(\infty\)
• Logarithm of odds maps them to \(-\infty\) to \(\infty\)

Logit Link Function - 1

• The Logit function is our link function
• \[g(\pi_i) = \log\frac{\pi_i}{1-\pi_i}\]

Logit Link Function - 2

• For standard regression:
• \[f(\mathbf{ x}_i) = \mathbf{ w}^\top \boldsymbol{ \phi}(\mathbf{ x}_i)\]

Logistic function - 3

• Logistic (or sigmoid) squashes real line to between 0 & 1. Sometimes also called a ‘squashing function.’

Logistic funciton - 4

• For classification (logistic regression): \[\log \frac{\pi_i}{1-\pi_i} = \mathbf{ w}^\top \boldsymbol{ \phi}(\mathbf{ x}_i)\]

Sigmoid Function

Prediction Function

Prediction Function

• Can write \(\pi\) as a function of input, parameters, \[\pi(\mathbf{ x},\mathbf{ w}) = \frac{1}{1+ \exp\left(-\mathbf{ w}^\top \boldsymbol{ \phi}(\mathbf{ x})\right)}.\]
• Compute the output \(\mathbf{ w}^\top \boldsymbol{ \phi}(\mathbf{ x})\)
• Apply inverse link function, \(h(\mathbf{ w}^\top \boldsymbol{ \phi}(\mathbf{ x}))\).
• Use this value in a Bernoulli distribution to form the likelihood.

Bernoulli Reminder

• From last time \[P(y_i|\mathbf{ w}, \mathbf{ x}) = \pi_i^{y_i} (1-\pi_i)^{1-y_i}\]

• Trick for switching betwen probabilities

def bernoulli(y, pi):
    if y == 1:
        return pi
    else:
        return 1-pi

Maximum Likelihood

• Conditional independence of data: \[P(\mathbf{ y}|\mathbf{ w}, \mathbf{X}) = \prod_{i=1}^nP(y_i|\mathbf{ w}, \mathbf{ x}_i). \]

Negative Log Likelihood

Objective Function

• Probability of positive outcome for the \(i\)th data point \[\pi_i = h\left(\mathbf{ w}^\top \boldsymbol{ \phi}(\mathbf{ x}_i)\right),\] where \(h(\cdot)\) is the inverse link function
• Objective function of the form \[\begin{align*} E(\mathbf{ w}) = & - \sum_{i=1}^ny_i \log h\left(\mathbf{ w}^\top \boldsymbol{ \phi}(\mathbf{ x}_i)\right) \\& - \sum_{i=1}^n(1-y_i)\log \left(1-h\left(\mathbf{ w}^\top \boldsymbol{ \phi}(\mathbf{ x}_i)\right)\right). \end{align*}\]

Minimise Objective

• Grdient wrt \(\pi(\mathbf{ x};\mathbf{ w})\) \[\begin{aligned} \frac{\text{d}E(\mathbf{ w})}{\text{d}\mathbf{ w}} = & -\sum_{i=1}^n\frac{y_i}{h\left(\mathbf{ w}^\top \boldsymbol{ \phi}(\mathbf{ x})\right)}\frac{\text{d}h(f_i)}{\text{d}f_i} \boldsymbol{ \phi}(\mathbf{ x}_i) \\ & + \sum_{i=1}^n \frac{1-y_i}{1-h\left(\mathbf{ w}^\top \boldsymbol{ \phi}(\mathbf{ x})\right)}\frac{\text{d}h(f_i)}{\text{d}f_i} \boldsymbol{ \phi}(\mathbf{ x}_i) \end{aligned}\]

Link Function Gradient

• Also need gradient of inverse link function wrt parameters. \[\begin{aligned} h(f_i) &= \frac{1}{1+\exp(-f_i)}\\ &=(1+\exp(-f_i))^{-1} \end{aligned}\]

Link Function Gradient

Objective Gradient

Objective Gradient

Multiplying everything out leads to \[ \begin{aligned} \frac{\text{d}E(\mathbf{ w})}{\text{d}\mathbf{ w}} = & -\sum_{i=1}^n y_i- h\left(\mathbf{ w}^\top \boldsymbol{ \phi}(\mathbf{ x})\boldsymbol{ \phi}(\mathbf{ x}_i). \]

Optimisation of the Function

• Can’t find a stationary point of the objective function analytically.
• Optimisation has to proceed by numerical methods.
  • Newton’s method or
  • gradient based optimisation methods
  • Iterative Reweighted Least Squares
• Similarly to matrix factorisation, for large data stochastic gradient descent (Robbins Munro (Robbins and Monro, 1951) optimisation procedure) works well.

Toy Data

• Red crosses (+ve) and green circles (-ve).

Logistic Regression vs Perceptron

\[ \mathbf{ w}_\text{new} \leftarrow \mathbf{ w}_\text{old} - \eta(H(\boldsymbol{ \phi}_i^\top \mathbf{ w}) (1-y_i) \boldsymbol{ \phi}_i - (1-H(\boldsymbol{ \phi}_i^\top \mathbf{ w})) y_i \boldsymbol{ \phi}_i \]

The gradient of the negative log-likelihood of logistic regression is \[ \frac{\text{d}E(\mathbf{ w})}{\text{d}\mathbf{ w}} = -\sum_{i=1}^n y_i\left(1-h\left(\mathbf{ w}^\top \boldsymbol{ \phi}_i\right)\right) \boldsymbol{ \phi}_i + \sum_{i=1}^n (1-y_i)\left(h\left(\mathbf{ w}^\top \boldsymbol{ \phi}_i\right)\right) \boldsymbol{ \phi}_i. \] so the gradient with respect to one point is \[ \frac{\text{d}E_i(\mathbf{ w})}{\text{d}\mathbf{ w}}=y_i\left(1-h\left(\mathbf{ w}^\top \boldsymbol{ \phi}_i\right)\right) \boldsymbol{ \phi}_i + (1-y_i)\left(h\left(\mathbf{ w}^\top \boldsymbol{ \phi}_i\right)\right) \boldsymbol{ \phi}_i. \] and the stochastic gradient update for logistic regression (with mini-batch size set to 1) is \[ \mathbf{ w}_\text{new} \leftarrow \mathbf{ w}_\text{old} - \eta ((1-y_i)\left(h\left(\mathbf{ w}^\top \boldsymbol{ \phi}_i\right)\right) - y_i\left(1-h\left(\mathbf{ w}^\top \boldsymbol{ \phi}_i\right)\right) \boldsymbol{ \phi}_i) \] The difference between the two is that for the perceptron we are using the Heaviside function, \(H(\cdot)\), whereas for logistic regression we’re using the sigmoid, \(h(\cdot)\), which is like a soft version of the Heaviside function.

❮ ❯

Nigeria NMIS Data

Nigeria NMIS Data: Notebook

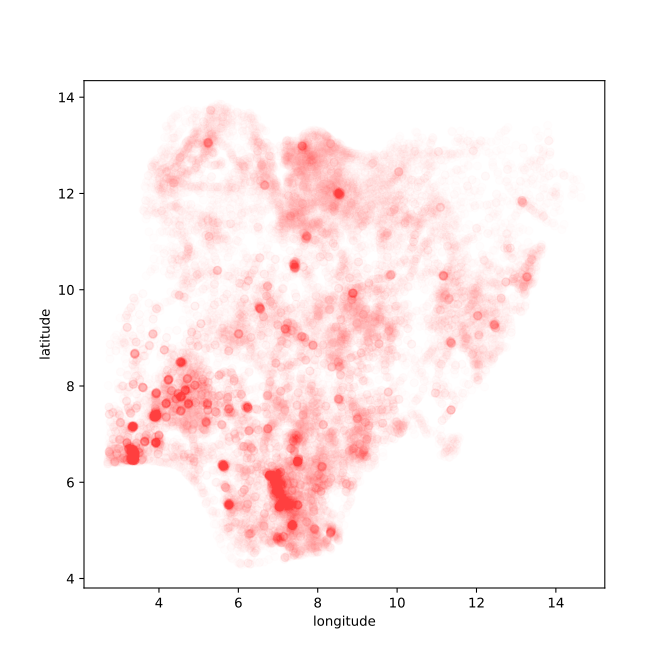
Nigeria NMIS Data Classification

Batch Gradient Descent

Stochastic Gradient Descent

Model Diagnostics and Linear Regression

Linear Regression Model

• Linear regression models continuous response \(y_i\) vs inputs \(\mathbf{ x}_i\): \[y_i = f(\mathbf{ x}_i) + \epsilon_i\] where \(f(\mathbf{ x}_i) = \mathbf{ w}^\top\mathbf{ x}_i\)

• Probabilistic model: \[p(y_i|\mathbf{ x}_i) = \mathscr{N}\left(y_i|\mathbf{ w}^\top\mathbf{ x}_i,\sigma^2\right)\]

Linear Regression in Matrix Form

• Matrix form: \[\mathbf{ y}= \mathbf{X}\mathbf{ w}+ \boldsymbol{ \epsilon}\]

• Expected prediction: \[\mathbb{E}[y_i|\mathbf{ x}_i] = \mathbf{ w}^\top\mathbf{ x}_i\]

Model Fit Statistics

• Model fit statistics help assess overall performance:
  • R-squared shows variance explained
  • F-statistic tests if model is useful
  • AIC/BIC help compare models

Parameter Estimates

• Parameter estimates tell us about relationships:
  • Coefficients show effect direction/size
  • Standard errors show uncertainty
  • \(p\)-values test significance

Residual Diagnostics

• Residual diagnostics check assumptions:
  • Tests for normality and autocorrelation
  • Look for patterns that violate assumptions

Visual Inspection

• Visual inspection is crucial:
  • With 1D data we can plot everything
  • Helps spot patterns statistics might miss
  • Shows if relationship makes practical sense

Linear Regression Fit

• 1904 St. Louis Olympics: Major outlier
  • Explains non-normal residuals
  • Contributes to right skew

Data Regimes

• Three distinct regimes visible:
  • Pre-WWI: Rapid improvement
  • War years: Disrupted progress
  • Post-WWII: Steady improvement

Model Improvements

• Model improvements possible with extra features:
  • Polynomial terms
  • Period indicators
  • Interaction terms
  • External factors

Design Matrix

• The design matrix \(\boldsymbol{ \Phi}\) stores our features
• Each row represents one data point
• Each column represents one feature
• For \(n\) data points and \(p\) features: \[\boldsymbol{ \Phi}= \begin{bmatrix} \phi_{11} & \phi_{12} & \cdots & \phi_{1p} \\ \phi_{21} & \phi_{22} & \cdots & \phi_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ \phi_{n1} & \phi_{n2} & \cdots & \phi_{np} \end{bmatrix}\]
• Also called the feature matrix or model matrix

Categorical (Multinomial) Regression

• Multi-class extension of logistic regression
• Model class scores with linear functions, convert to probabilities via softmax

Soft Arg Max (Softmax) Function

• Softmax turns unnormalised scores into probabilities
• Invariant to adding a constant to all scores

Prediction Function

Prediction Function

• Class scores: \(f_k(\mathbf{ x})=\mathbf{ w}_k^\top\boldsymbol{ \phi}(\mathbf{ x})\)
• Probabilities via softmax: \(\pi_k = \exp(f_k)/\sum_j \exp(f_j)\)

Maximum Likelihood

• Conditional independence: \(P(\mathbf{ y}|\{\mathbf{ w}_k\}, \mathbf{X})=\prod_i P(y_i|\{\mathbf{ w}_k\},\mathbf{ x}_i)\)

Objective Function

• One-hot targets \(\mathbf{ y}_i\), softmax probabilities \(\pi_{ik}\)
• Negative log-likelihood: \(E = -\sum_i \sum_k y_{ik}\log\pi_{ik}\)

Other GLMs

• Logistic regression is part of a family known as generalized linear models
• They all take the form \[g^{-1}(f_i(x)) = \mathbf{ w}^\top \boldsymbol{ \phi}(\mathbf{ x}_i)\]
• Other examples include Poisson regression.

Other GLMs

• Logistic regression is part of a family known as generalised linear models
• They all take the form \[g^{-1}(f_i(x)) = \mathbf{ w}^\top \boldsymbol{ \phi}(\mathbf{ x}_i)\]
• Other examples include Poisson regression.

Poisson Distribution

• Poisson distribution is used for ‘count data.’ For non-negative integers, \(y\), \[P(y) = \frac{\lambda^y}{y!}\exp(-y)\]
• Here \(\lambda\) is a rate parameter that can be thought of as the number of arrivals per unit time.
• Poisson distributions can be used for disease count data. E.g. number of incidence of malaria in a district.

Poisson Distribution

Poisson Regression

• In a Poisson regression make rate a function of space/time. \[\log \lambda(\mathbf{ x}, t) = \mathbf{ w}_x^\top \boldsymbol{ \phi}_x(\mathbf{ x}) + \mathbf{ w}_t^\top \boldsymbol{ \phi}_t(t)\]
• This is known as a log linear or log additive model.
• The link function is a logarithm.
• We can rewrite such a function as \[\log \lambda(\mathbf{ x}, t) = f_x(\mathbf{ x}) + f_t(t)\]

Multiplicative Model

• Be careful though … a log additive model is really multiplicative. \[\log \lambda(\mathbf{ x}, t) = f_x(\mathbf{ x}) + f_t(t)\]
• Becomes \[\lambda(\mathbf{ x}, t) = \exp(f_x(\mathbf{ x}) + f_t(t))\]
• Which is equivalent to \[\lambda(\mathbf{ x}, t) = \exp(f_x(\mathbf{ x}))\exp(f_t(t))\]
• Link functions can be deceptive in this way.

Synthetic Example

Poisson Regression Diagnostics

The Exponential Family

Exponential Family Regression

{For this form the gradient of the log likelihood with respect to the model’s parameters is given by \[ \nabla_\mathbf{W}L(\mathbf{W}) = \left(T- \left\langle T\right\rangle_{p(\mathbf{ y}|\boldsymbol{ \theta})})\boldsymbol{ \Phi}. \]

Bernoulli as Exponential Family

Categorical Distribution as Exponental Family

Gaussian as Exponential Family

{The natural parameters of a univariate Gaussian with mean, \(\mu\) and variance \(\sigma^2\), \[ y \sim \mathscr{N}\left((,\mu\right), \sigma^2) \] are \(\theta_1 = \frac{\mu}{\sigma^2}\) and \(\theta_2 = -\tfrac{1}{2\sigma^2}\). This allows us to write \[ p(y | \boldsymbol{ \theta}) = \exp(\nu_1 y + \nu_2 y^2 - A(\boldsymbol{ \theta}) \] where the log partition function is \[ A(\theta_1, \theta_2) = \frac{\theta_1^2}{4\theta_2} - \frac{1}{2}\log\det{-2\theta_2} - \frac{1}{2}\log 2\pi. \]

Poisson Distribution in Exponential Family Form

Practical Tips

{

• Feature engineering is critical
• Build modular pipelines to test features
• Consider interactions between variables
• Document your process carefully

Model Validation

• Use cross-validation wisely
• Bootstrap for uncertainty
• Keep hold-out test sets
• Beware of temporal leakage

Diagnostic Checks

Diagnostic checks are essential for building confidence about the model reliability. Create residual plots against fitted values and each predictor. Look for systematic patterns, a U-shaped residual plot suggests missing quadratic terms. For logistic regression, plot predicted probabilities against actual outcomes in bins to check calibration. Calculate influence measures like Cook’s distance to identify outliers. In a house price model, a mansion might have outsized influence on coefficients. Check variance inflation factors (VIF) for multicollinearity. High VIF (>5-10) suggests problematic correlation between predictors.

• Plot residuals systematically
• Check for non-linear patterns
• Identify influential points
• Test feature relationships

Visualisation

• Always plot raw data first
• Create diagnostic visualisations
• Check model assumptions
• Communicate results clearly