Week 5: Visualisation I: Discrete and Continuous Latent Variables

[jupyter][google colab][reveal]

Neil D. Lawrence

Abstract:

This lecture introduces different approaches to discovering latent structure in data. We begin by examining clustering as a discrete approach to finding latent structure, then explore why high dimensional data often has simpler underlying continuous representations. This motivates our introduction to Principal Component Analysis (PCA) as a fundamental approach to continuous latent variable modeling.

Setup

notutils

This small package is a helper package for various notebook utilities used below.

The software can be installed using

%pip install notutils

from the command prompt where you can access your python installation.

The code is also available on GitHub: https://github.com/lawrennd/notutils

Once notutils is installed, it can be imported in the usual manner.

import notutils

pods

In Sheffield we created a suite of software tools for ‘Open Data Science’. Open data science is an approach to sharing code, models and data that should make it easier for companies, health professionals and scientists to gain access to data science techniques.

You can also check this blog post on Open Data Science.

The software can be installed using

%pip install pods

from the command prompt where you can access your python installation.

The code is also available on GitHub: https://github.com/lawrennd/ods

Once pods is installed, it can be imported in the usual manner.

import pods

mlai

The mlai software is a suite of helper functions for teaching and demonstrating machine learning algorithms. It was first used in the Machine Learning and Adaptive Intelligence course in Sheffield in 2013.

The software can be installed using

%pip install mlai

from the command prompt where you can access your python installation.

The code is also available on GitHub: https://github.com/lawrennd/mlai

Once mlai is installed, it can be imported in the usual manner.

import mlai
from mlai import plot

Visualization and Human Perception

The human visual system is remarkable - it represents our highest bandwidth connection to the world around us, with the optic tract carrying around 8.75 million bits per second of information to our brain (Koch et al., 2006). The “nerve” is misnamed, it is actually an extension of brain tissue, highlighting how central vision is to our cognitive architecture. Our (bidrectional) verbal communication is limited to around 2,000 bits per minute, but our eyes actively grab at information from our environment at vastly higher rates. This “active sensing” approach, see e.g. MacKay (1991) and O’Regan (2011), means we don’t passively receive visual information but actively construct our understanding through rapid eye movements called saccades that sample our environment hundreds of times per second.

Behind the Eye

Figure: Behind the Eye (MacKay, 1991) summarises MacKay’s Gifford Lectures, where MacKay uses the operation of the eye as a window on the operation of the brain.

The high-bandwidth visual channel makes visualization a powerful tool for communication and understanding. But it also makes us vulnerable to manipulation through misleading. Just as social media algorithms can manipulate our behavior through careful curation of information, indeed they sometimes manipulate us through our visual system, poorly designed or deliberately deceptive visualizations can lead us to incorrect conclusions by hijacking our natural visual processing capabilities.

Figure: Kevin O’Regan’s book, “Why Red Doesn’t Sound Like a Bell” is about the sensiorimotor perspective on feel and ranges from our senses to our consciousness.

The book, “Why Red Doesn’t Sound Like a Bell” by J. Kevin O’Regan (O’Regan, 2011) suggests a sensorimotor approach to understanding our consciousness. One that depends on how our senses interact with the world around us. The implication is that our consciousness is as much a function of our environment as of our mind. This is particularly interesting for social interaction, where our external environment is populated by other intelligent entities. If we accept this interpretation it would imply that we should pay a lot of attention to modes of human to human interaction when developing environments in which we can feel comfortable and able to perform.

In this lecture we’ll introduce the basics of visualisation through the lens of dimensionality reduction - techniques that help us represent high-dimensional data.

See Lawrence (2024) bandwidth, communication p. 10-12,16,21,29,31,34,38,41,44,65-67,76,81,90-91,104,115,149,196,214,216,235,237-238,302,334. See Lawrence (2024) MacKay, Donald p. 227-228,230-237,267-270. See Lawrence (2024) optic nerve/tract p. 205,235. See Lawrence (2024) O’Regan, Kevin p. 236-240,250,259,262-263,297,299. See Lawrence (2024) saccade p. 236,238,259-260,297,301. See Lawrence (2024) visual system/visual cortex p. 204-206,209,235-239,249-250,255,259,260,268-270,281,294,297,301,324,330.

Part 1: Discrete Latent Variables

Clustering

• Common approach for grouping data points
• Assigns data points to discrete groups
• Examples include:
  • Animal classification
  • Political affiliation grouping

Clustering is a common approach to data analysis, though we will not cover it in great depth in this course. The fundamental idea is to associate each data point \(\mathbf{ y}_{i, :}\) with one of \(k\) different discrete groups. This approach raises interesting questions - for instance, when clustering animals into groups, we might ask whether animal traits are truly discrete or continuous in nature. Similar questions arise when clustering political affiliations.

Humans seem to have a natural affinity for discrete clustering approaches. This makes clustering particularly useful when collaborating with biologists, who often think in terms of discrete categories. However, we should be mindful that this preference for discrete categories may sometimes oversimplify continuous variations in data.

• Clustering expects gaps between groups in data density
• Vector quantization may not require density gaps
• For practical purposes, both involve:
  • Allocating points to groups
  • Determining optimal number of groups

There is a subtle but important distinction between clustering and vector quantisation. In true clustering, we typically expect to see reductions in data density between natural groups - essentially, gaps in the data that separate different clusters. This definition isn’t universally applied though, and vector quantization may partition data without requiring such density gaps. For our current discussion, we’ll treat them similarly, focusing on the common challenges they share: how to allocate points to groups and, more challengingly, how to determine the optimal number of groups.

• Simple iterative clustering algorithm
• Key steps:
  1. Initialize with random centers
  2. Assign points to nearest center
  3. Update centers as cluster means
  4. Repeat until stable

The \(k\)-means algorithm provides a straightforward approach to clustering data. It requires two key elements: a set of \(k\) cluster centres and a way to assign each data point to a cluster. The algorithm follows a simple iterative process:

1. First, initialize cluster centres by randomly selecting \(k\) data points
2. Assign each data point to its nearest cluster centre
3. Update each cluster centre by computing the mean of all points assigned to it
4. Repeat steps 2 and 3 until the cluster assignments stop changing

This process is intuitive and relatively easy to implement, though it comes with certain limitations.

• Minimizes sum of squared distances: \[ E=\sum_{j=1}^K \sum_{i\ \text{allocated to}\ j} \left(\mathbf{ y}_{i, :} - \boldsymbol{ \mu}_{j, :}\right)^\top\left(\mathbf{ y}_{i, :} - \boldsymbol{ \mu}_{j, :}\right) \]
• Solution not guaranteed to be global or unique
• Represents a non-convex optimization problem

The \(k\)-means algorithm works by minimizing an objective function that measures the sum of squared Euclidean distances between each point and its assigned cluster center. This objective function can be written mathematically as shown above, where \(\boldsymbol{ \mu}_{j, :}\) represents the mean of cluster \(j\).

It’s important to understand that while this algorithm will always converge to a minimum, this minimum is not guaranteed to be either global or unique. The optimization problem is non-convex, meaning there can be multiple local minima. Different initializations of the cluster centers can lead to different final solutions, which is one of the key challenges in applying \(k\)-means clustering in practice.

import mlai
import numpy as np
import os

Clustering methods associate data points with different labels that are allocated by the computer rather than provided by human annotators. This process is quite intuitive for humans - we naturally cluster our observations of the real world. For example, we cluster animals into groups like birds, mammals, and insects. While these labels can be provided by humans, they were originally invented through a clustering process. With computational clustering, we want to recreate that process of label invention.

When thinking about ideas, the Greek philosopher Plato considered the concept of Platonic ideals - the most quintessential version of a thing, like the most bird-like bird or chair-like chair. In clustering, we aim to define different categories by finding their Platonic ideals (cluster centers) and allocating each data point to its nearest center. This allows computers to form categorizations of data at scales too large for human processing.

To implement clustering computationally, we need to mathematically represent both our objects and cluster centers as vectors (\(\mathbf{ x}_i\) and \(\boldsymbol{ \mu}_j\) respectively) and define a notion of either similarity or distance between them. The distance function \(d_{ij} = f(\mathbf{ x}_i, \boldsymbol{ \mu}_j)\) measures how far each object is from potential cluster centers. For example, we might cluster customers by representing them through their purchase history and measuring their distance to different customer archetypes.

Squared Distance

A commonly used distance metric is the squared distance: \(d_{ij} = (\mathbf{ x}_i - \boldsymbol{ \mu}_j)^2\). This metric appears frequently in machine learning - we saw it earlier measuring prediction errors in regression, and here it measures dissimilarity between data points and cluster centers.

Once we have decided on the distance or similarity function, we can decide a number of cluster centers, \(K\). We find their location by allocating each center to a sub-set of the points and minimizing the sum of the squared errors, \[ E(\mathbf{M}) = \sum_{i \in \mathbf{i}_j} (\mathbf{ x}_i - \boldsymbol{ \mu}_j)^2 \] where the notation \(\mathbf{i}_j\) represents all the indices of each data point which has been allocated to the \(j\)th cluster represented by the center \(\boldsymbol{ \mu}_j\).

\(k\)-Means Clustering

One approach to minimizing this objective function is known as \(k\)-means clustering. It is simple and relatively quick to implement, but it is an initialization sensitive algorithm. Initialization is the process of choosing an initial set of parameters before optimization. For \(k\)-means clustering you need to choose an initial set of centers. In \(k\)-means clustering your final set of clusters is very sensitive to the initial choice of centers. For more technical details on \(k\)-means clustering you can watch a video of Alex Ihler introducing the algorithm here.

\(k\)-Means Clustering

Figure: Clustering with the \(k\)-means clustering algorithm.

Figure: \(k\)-means clustering by Alex Ihler.

Hierarchical Clustering

Other approaches to clustering involve forming taxonomies of the cluster centers, like humans apply to animals, to form trees. Hierarchical clustering builds a tree structure showing the relationships between data points. We’ll demonstrate agglomerative clustering on the oil flow data set, which contains measurements from a multiphase flow facility.

Oil Flow Data

This data set is from a physics-based simulation of oil flow in a pipeline. The data was generated as part of a project to determine the fraction of oil, water and gas in North Sea oil pipes (Bishop:gtm96?).

import pods

data = pods.datasets.oil()

The data consists of 1000 12-dimensional observations of simulated oil flow in a pipeline. Each observation is labelled according to the multi-phase flow configuration (homogeneous, annular or laminar).

# Convert data["Y"] from [1, -1, -1] in each row to rows of 0 or 1 or 2
Y = data["Y"]
# Find rows with 1 in first column (class 0)
class0 = (Y[:, 0] == 1).astype(int) * 0
# Find rows with 1 in second column (class 1) 
class1 = (Y[:, 1] == 1).astype(int) * 1
# Find rows with 1 in third column (class 2)
class2 = (Y[:, 2] == 1).astype(int) * 2
# Combine into single array of class labels 0,1,2
data["Y"] = class0 + class1 + class2

} The data is returned as a dictionary containing training and test inputs (‘X’, ‘Xtst’), training and test labels (‘Y’, ‘Ytst’), and the names of the features.

Figure: Visualization of the first two dimensions of the oil flow data from (Bishop-oil93?)

As normal we include the citation information for the data.

print(data['citation'])

And extra information about the data is included, as standard, under the keys info and details.

print(data['details'])

X = data['X']
Y = data['Y']

import numpy as np
from scipy.cluster.hierarchy import dendrogram, linkage
import pods

# Perform hierarchical clustering
linked = linkage(X, 'ward')  # Ward's method for minimum variance

Figure: Hierarchical clustering applied to oil flow data. The dendrogram shows how different flow regimes are grouped based on their measurement similarities. The three main flow regimes (homogeneous, annular, and laminar) should form distinct clusters.

In this example, we’ve applied hierarchical clustering to the oil flow data set. The data contains measurements from different flow regimes in a multiphase flow facility. The dendrogram shows how measurements naturally cluster into different flow types. Ward’s linkage method is used as it tends to create compact, evenly-sized clusters. You can learn more about agglomerative clustering in this video from Alex Ihler.

Figure: Hierarchical Clustering by Alex Ihler.

Phylogenetic Trees

A powerful application of hierarchical clustering is in constructing phylogenetic trees from genetic sequence data. By comparing DNA/RNA sequences across species, we can reconstruct their evolutionary relationships and estimate when species diverged from common ancestors. The resulting tree structure, called a phylogeny, maps out the evolutionary history and relationships between organisms.

Modern phylogenetic methods go beyond simple clustering - they incorporate sophisticated models of genetic mutation and molecular evolution. These models can estimate not just the structure of relationships, but also the timing of evolutionary divergence events based on mutation rates. This has important applications in tracking the origins and spread of rapidly evolving pathogens like HIV and influenza viruses. Understanding viral phylogenies helps epidemiologists trace outbreak sources, track transmission patterns, and develop targeted containment strategies.

Product Clustering

An e-commerce company could apply hierarchical clustering to organize their product catalog into a taxonomy tree. Products would be grouped into increasingly specific categories - for example, Electronics might split into Phones, Computers, etc., with Phones further dividing into Smartphones, Feature Phones, and so on. This creates an intuitive hierarchical organization. However, many products naturally belong in multiple categories - for instance, running shoes could reasonably be classified as both sporting equipment and footwear. The strict tree structure of hierarchical clustering doesn’t allow for this kind of multiple categorization, which is a key limitation for product organization.

Hierarchical Clustering Challenge

Our psychological ability to form categories is far more sophisticated than hierarchical trees. Research in cognitive science has revealed that humans naturally form overlapping categories and learn abstract principles that guide classification. Josh Tenenbaum’s influential work demonstrates how human concept learning combines multiple forms of inference through hierarchical Bayesian models that integrate similarity-based clustering with theory-based reasoning. This computational approach aligns with foundational work by Eleanor Rosch on prototype theory and Susan Carey’s research on conceptual change, showing how categorization adapts to context and goals. While these cognitively-inspired models better capture human-like categorization, their computational complexity currently limits practical applications to smaller datasets. Nevertheless, they provide important insights into more flexible clustering approaches that could eventually enhance machine learning systems.

Other Clustering Approaches

Spectral clustering (Shi and Malik (2000),Ng et al. (n.d.)) is a powerful technique that uses eigenvalues of similarity matrices to perform dimensionality reduction before clustering. Unlike k-means, it can identify clusters of arbitrary shape, making it effective for complex data like image segmentation or social networks.

The Dirichlet process provides a Bayesian framework for clustering without pre-specifying the number of clusters. It’s particularly valuable in scenarios where new, previously unseen categories may emerge over time. For example, in species discovery, it can model the probability of finding new species while accounting for known ones. This “infinite clustering” property makes it well-suited for open-ended learning problems where the total number of categories is unknown.

Part 2: Continuous Latent Variables

High Dimensional Data

To introduce high dimensional data, we will first of all introduce a hand written digit from the U.S. Postal Service handwritten digit data set (originally collected from scanning enveolopes) and used in the first convolutional neural network paper (Le Cun et al., 1989).

Le Cun et al. (1989) downscaled the images to \(16 \times 16\), here we use an image at the original scale, containing 64 rows and 57 columns. Since the pixels are binary, and the number of dimensions is 3,648, this space contains \(2^{3,648}\) possible images. So this space contains a lot more than just one digit.

USPS Samples

If we sample from this space, taking each pixel independently from a probability which is given by the number of pixels which are ‘on’ in the original image, over the total number of pixels, we see images that look nothing like the original digit.

Figure: Even if we sample every nano second from now until the end of the universe we won’t see the original six again.

Even if we sample every nanosecond from now until the end of the universe you won’t see the original six again.

Simple Model of Digit

So, an independent pixel model for this digit doesn’t seem sensible. The total space is enormous, and yet the space occupied by the type of data we’re interested in is relatively small.

Consider a different type of model. One where we take a prototype six and we rotate it left and right to create new data.

%pip install scikit-image

Figure: Rotate a prototype six to form a set of plausible sixes.

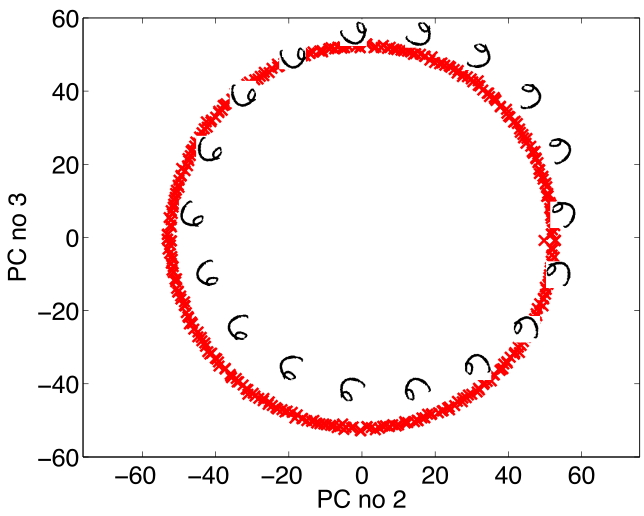
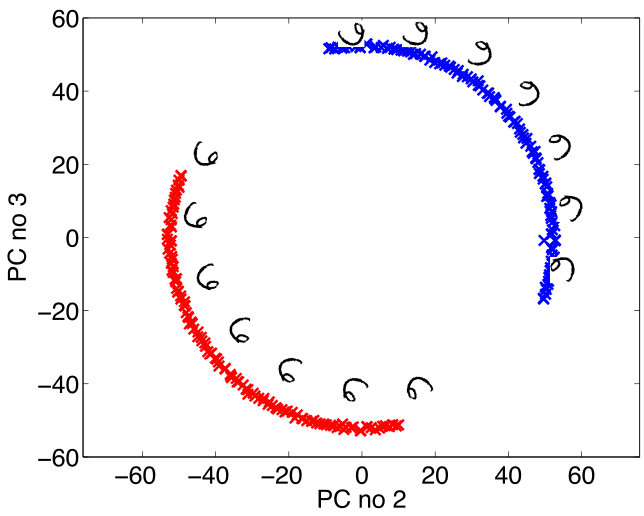
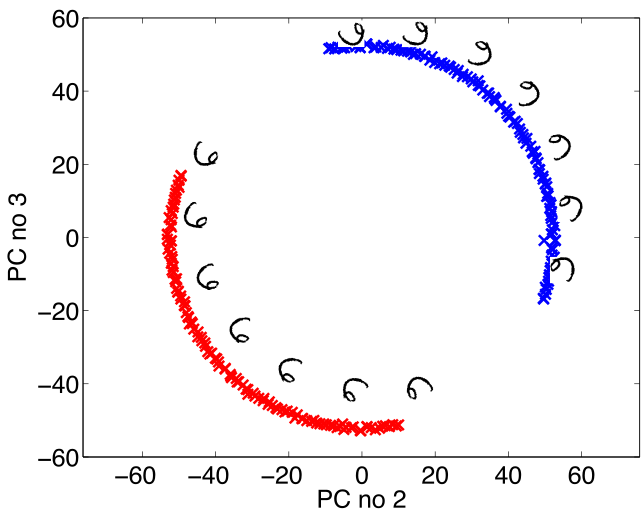
Figure: The rotated sixes projected onto the first two principal components of the ‘rotated data set’. The data lives on a one dimensional manifold in the 3,648 dimensional space.

Low Dimensional Manifolds

Of course, in practice pure rotation of the image is too simple a model. Digits can undergo several distortions and retain their nature. For example, they can be scaled, they can go through translation, they can udnergo ‘thinning’. But, for data with ‘structure’ we expect fewer of these distortions than the dimension of the data. This means we expect data to live on a lower dimensonal manifold. This implies that we should deal with high dimensional data by looking for a lower dimensional (non-linear) embedding.

High Dimensional Data Effects

In high dimensional spaces, our intuitions from everyday three dimensional space can fail dramatically. There are two major effects that occur:

1. All data moves to a “shell” at one standard deviation from the mean (known as the “curse of dimensionality”)
2. Distances between points become constant

Let’s explore these effects with some experiments.

import numpy as np
import mlai.plot as plot
import matplotlib.pyplot as plt
import mlai

# Generate high-dimensional Gaussian data
d = 1000  # dimensions
n = 100   # number of points
Y = np.random.normal(size=(n, d))

fig, ax = plt.subplots(figsize=plot.big_wide_figsize)
plot.distance_distribution(Y, title=f'Distance Distribution for {d}-D Gaussian Data', ax=ax)
mlai.write_figure('high-d-distances.svg', directory='./dimred')

Figure: Distribution of pairwise distances between points in high-dimensional Gaussian data. The red line shows the theoretical gamma distribution.

This plot shows the distribution of pairwise distances between points in our high-dimensional Gaussian data. The red line shows the theoretical prediction - a gamma distribution with shape parameter d/2 and scale 2/d. The close match between theory and practice demonstrates how in high dimensions, distances between random points become highly concentrated around a particular value.

Structured High Dimensional Data

Now let’s look at what happens when we introduce structure into our high-dimensional data. We’ll create data that actually lies in a lower-dimensional space, but embedded in high dimensions.

# Generate data that lies on a 2D manifold embedded in 1000D
W = np.random.normal(size=(d, 2))  # 2D latent directions
latent = np.random.normal(size=(n, 2))  # 2D latent points
Y_structured = latent @ W.T  # Project to high dimensions

fig, ax = plt.subplots(figsize=plot.big_wide_figsize)
plot.distance_distribution(Y_structured, 
                         title='Distance Distribution for Structured High-D Data', 
                         ax=ax)
mlai.write_figure('structured-high-d-distances.svg', directory='./dimred')

Figure: Distribution of pairwise distances for structured high-dimensional data. The distribution differs significantly from pure high-dimensional data, reflecting the underlying 2D structure.

Notice how the distance distribution for the structured data deviates significantly from what we would expect for truly high-dimensional data. Instead of matching the theoretical curve for 1000-dimensional data, it more closely resembles what we would expect for 2-dimensional data. This is because despite living in a 1000-dimensional space, the data actually has an intrinsic dimensionality of 2.

This effect is exactly what we observe in real datasets - they typically have much lower intrinsic dimensionality than their ambient dimension would suggest. This is why dimensionality reduction techniques like PCA can be so effective: they help us discover and work with this lower-dimensional structure.

Exercise 1

Generate your own high-dimensional dataset with known structure and visualize its distance distribution. Try varying the intrinsic dimensionality (e.g. use 3D or 4D latent space) and observe how the distance distribution changes. What happens if you add some noise to the structured data?

High Dimensional Effects in Real Data

We’ve seen how high-dimensional random data behaves in a very specific way, with highly concentrated distance distributions. Now let’s examine some real datasets to see how they differ.

import numpy as np
import mlai.plot as plot
import matplotlib.pyplot as plt
import pods

First let’s look at a motion capture dataset, which despite having high dimension, is constrained by the physics of human movement.

data = pods.datasets.osu_run1()
Y = data['Y']

fig, ax = plt.subplots(figsize=plot.big_wide_figsize)
plot.distance_distribution(Y, title='Distance Distribution for Motion Capture Data', ax=ax)

Notice how the distance distribution is much more spread out than we would expect for random high-dimensional data. This suggests that the motion capture data has much lower intrinsic dimensionality than its ambient dimension, due to the physical constraints of human movement.

Oil Flow Data

Now let’s look at the oil flow dataset, which contains measurements from gamma densitometry sensors.

data = pods.datasets.oil()
Y = data['X']

fig, ax = plt.subplots(figsize=plot.big_wide_figsize)
plot.distance_distribution(Y, title='Distance Distribution for Oil Flow Data', ax=ax)

Again we see a deviation from what we would expect for random high-dimensional data. The oil flow data shows clear structure in its distance distribution, reflecting the physical constraints of fluid dynamics that govern the system.

Implications for Dimensionality Reduction

These examples demonstrate why dimensionality reduction can be so effective on real datasets:

1. Real data typically has strong constraints (physical, biological, economic, etc.) that restrict it to a lower-dimensional manifold
2. This manifold structure is revealed by the distribution of pairwise distances
3. Dimensionality reduction techniques like PCA can discover and exploit this structure

When we see a distance distribution that deviates from theoretical predictions for random high-dimensional data, it suggests that dimensionality reduction might be particularly effective.

Latent Variables and Dimensionality Reduction

Why does dimensionality reduction work on real data? The key insight is that while our measurements may be very high-dimensional, the underlying phenomena we’re measuring often have much lower intrinsic dimensionality. For example:

1. A motion capture recording might have hundreds of coordinates, but these are all generated by a person’s movements that have far fewer degrees of freedom.

2. Genetic data may record thousands of gene expression levels, but these are often controlled by a much smaller number of regulatory processes.

3. Images contain millions of pixels, but the actual meaningful content often lies on a much lower-dimensional manifold.

import numpy as np
import matplotlib.pyplot as plt
import mlai.plot as plot
import mlai

# Example showing how a 1D curve appears in 2D
t = np.linspace(0, 2*np.pi, 100)
x = np.column_stack([np.cos(t), np.sin(t)])

# Plot the data
fig, ax = plt.subplots(1, 2, figsize=plot.big_wide_figsize)
ax[0].plot(x[:, 0], x[:, 1], 'b.') 
ax[0].set_xlabel('$x_1$')
ax[0].set_ylabel('$x_2$')

# Plot the latent variable representation 
ax[1].plot(t, np.zeros_like(t), 'r.')
ax[1].set_xlabel('$z$')
ax[1].set_yticks([])

mlai.write_figure('latent-variable-example.svg', directory='./dimred')

Figure: Data that appears 2-dimensional (left) can be described by a single latent variable \(z\) (right) that traces out the curve.

This example shows how data that appears to be 2-dimensional (left) can actually be described by a single latent variable \(z\) (right) that traces out the curve. The key premise of dimensionality reduction is finding and working with these simpler underlying representations.

Latent Variables

Latent means hidden, and hidden variables are simply unobservable variables. The idea of a latent variable is crucial to the concept of artificial intelligence, machine learning and experimental design. A latent variable could take many forms. We might observe a man walking along a road with a large bag of clothes and we might infer that the man is walking to the laundrette. Our observations are a highly complex data space, the response in our eyes is processed through our visual cortex, the combination of the individual’s limb movememnts and the direction they are walking in all conflate in our heads to cause us to infer that (perhaps) the individual is going to the laundrette. We don’t know that the man is walking to the laundrette, but we have a model of the world that suggests that it’s a likely outcome for the very complex data. In some ways the latent variable can be seen as a compression of this very complex scene. If I were writing a book, I might write that “A man tripped over whilst walking to the laundrette”. In the reader’s mind an image of a man, perhaps laden with dirty clothes, may occur. All these ideas come from our expectations of the world around us. We can make further inference about the man, some of it perhaps plausible others less so. The man may be going to the laundrette because his washing machine is broken, or because he doesn’t have a large enough flat to have a washing machine, or because he’s carrying a duvet, or because he doesn’t like ironing. All of these may increase in probability given our observation, but they are still latent variables. Unless we follow the man back to his appartment, or start making other enquirires about the man, we don’t know the true answer.

It’s clear that to do inference about any complex system we must include latent variables. Latent variables are extremely powerful. In robotics, they are used to represent the state of the robot. The state of the robot may include its position (in x, y coordinates) its speed, its direction of facing. How are these variables unknown to the robot? Well the robot only posesses sensors, it can make observations of the nearest object in a certain direction, and it may have a map of its environment. If we represent the state of the robot as its position on a map, it may be uncertain of that position. If you go walking or running in the hills around Sheffield, you can take a very high quality ordnance survey map with you. However, unless you are a really excellent orienteer, when you are far from any given landmark, you will probably be uncertain about your true position on the map. These states are also latent variables.

In statistical analysis of experiments you try to control for each aspect of the experiment, in particular by randomization. So if I’m interested in the ability of a particular fertilizer to improve the yield of a particular plant I may design an experiment where I apply the fertilizer to some plants (the treatment group) and withold the fertilizer from others (the control group). I then test to see whether the yield from the treatment group is better (or worse) than the control group. I may find that I have an excellent yield for the treatment group. However, what if I’d (unknowlingly) planted all my treatment plants in a sunny part of the field, and all the control plants in a shady part of the field. That would also be a latent variable, in this case known as a confounder. In statistical experimental design randomization is used to attempt to eliminate the correlated effects of these confounders: you aim to ensure that if these confounders do exist their effects are not correlated with treatment and contorl. This is known as a randomized control trial.

Greek philosophers worried a great deal about what was knowable and what was unknowable. Adherents of philosophical Skeptisism were inspired by the idea that since your senses sometimes give you contradictory information, they cannot be trusted, and in extreme cases they chose to ignore their senses. This is an acknowledgement that very often the true state of the world cannot be known with precision. Unfortunately, these philosophers didn’t have a good understanding of probability, so they were unable to encapsulate their ideas through a degree of belief.

We often use language to express the compression of a complex behavior or patterns in a simpler way, for example we talk about motives as a useful distallation for a perhaps very complex patter of behavior. In physics we use principles of causation and simple laws to describe the world around us. Such motives or underlying principles are difficult to observe directly, our conclusions about them emerge over a period of time by observing indirect consequences of the latent variables.

Epistemic uncertainty allows us to deal with these worries by associating our degree of belief about the state of the world with a probaiblity distribution. This core idea underpins state space modelling, probabilistic graphical models and the wider field of latent variable modelling. In this session we are going to explore the idea in a simple linear system and see how it relates to factor analysis and principal component analysis.

Your Personality

At the beginning of the 20th century there was a great deal of interest amoungst psychologists in formalizing patterns of thought. The approach they used became known as factor analysis. The principle is that we observe a potentially high dimensional vector of characteristics about an individual. To formalize this, social scientists designed questionaires. We can envisage many questions that we may ask, but the assumption is that underlying these questions there are only a few traits that dictate the behavior. These models are known as latent trait models and the analysis is sometimes known as factor analysis. The idea is that there are a few characteristic traits that we are looking to discern. These traits or factors can be extracted by assimilating the high dimensional characteristics of the individual into a few latent factors.

Factor Analysis Model

This causes us to consider a model as follows, if we are given a high dimensional vector of features (perhaps questionaire answers) associated with an individual, \(\mathbf{ y}\), we assume that these factors are actually generated from a low dimensional vector latent traits, or latent variables, which determine the personality. \[ \mathbf{ y}= \mathbf{f}(\mathbf{ z}) + \boldsymbol{ \epsilon}, \] where \(\mathbf{f}(\mathbf{ z})\) is a vector valued function that is dependent on the latent traits and \(\boldsymbol{ \epsilon}\) is some corrupting noise. For simplicity, we assume that the function is given by a linear relationship, \[ \mathbf{f}(\mathbf{ z}) = \mathbf{W}\mathbf{ z} \] where we have introduced a matrix \(\mathbf{W}\) that is sometimes referred to as the factor loadings but we also immediately see is related to our multivariate linear regression models from the . That is because our vector valued function is of the form

\[ \mathbf{f}(\mathbf{ z}) = \begin{bmatrix} f_1(\mathbf{ z}) \\ f_2(\mathbf{ z}) \\ \vdots \\ f_p(\mathbf{ z})\end{bmatrix} \] where there are \(p\) features associated with the individual. If we consider any of these functions individually we have a prediction function that looks like a regression model, \[ f_j(\mathbf{ z}) = \mathbf{ w}_{j, :}^\top \mathbf{ z}, \] for each element of the vector valued function, where \(\mathbf{ w}_{:, j}\) is the \(j\)th column of the matrix \(\mathbf{W}\). In that context each column of \(\mathbf{W}\) is a vector of regression weights. This is a multiple input and multiple output regression. Our inputs (or covariates) have dimensionality greater than 1 and our outputs (or response variables) also have dimensionality greater than one. Just as in a standard regression, we are assuming that we don’t observe the function directly (note that this also makes the function a type of latent variable), but we observe some corrupted variant of the function, where the corruption is given by \(\boldsymbol{ \epsilon}\). Just as in linear regression we can assume that this corruption is given by Gaussian noise, where the noise for the \(j\)th element of \(\mathbf{ y}\) is by, \[ \epsilon_j \sim \mathcal{N}\left(0,\sigma^2_j\right). \] Of course, just as in a regression problem we also need to make an assumption across the individual data points to form our full likelihood. Our data set now consists of many observations of \(\mathbf{ y}\) for diffetent individuals. We store these observations in a design matrix, \(\mathbf{Y}\), where each row of \(\mathbf{Y}\) contains the observation for one individual. To emphasize that \(\mathbf{ y}\) is a vector derived from a row of \(\mathbf{Y}\) we represent the observation of the features associated with the \(i\)th individual by \(\mathbf{ y}_{i, :}\), and place each individual in our data matrix,

\[ \mathbf{Y} = \begin{bmatrix} \mathbf{ y}_{1, :}^\top \\ \mathbf{ y}_{2, :}^\top \\ \vdots \\ \mathbf{ y}_{n, :}^\top\end{bmatrix}, \] where we have \(n\) data points. Our data matrix therefore has \(n\) rows and \(p\) columns. The point to notice here is that each data obsesrvation appears as a row vector in the design matrix (thus the transpose operation inside the brackets). Our prediction functions are now actually a matrix value function, \[ \mathbf{F} = \mathbf{Z}\mathbf{W}^\top, \] where for each matrix the data points are in the rows and the data features are in the columns. This implies that if we have \(q\) inputs to the function we have \(\mathbf{F}\in \Re^{n\times p}\), \(\mathbf{W}\in \Re^{p \times q}\) and \(\mathbf{Z}\in \Re^{n\times q}\).

Exercise 2

Show that, given all the definitions above, if, \[ \mathbf{F} = \mathbf{Z}\mathbf{W}^\top \] and the elements of the vector valued function \(\mathbf{F}\) are given by \[ f_{i, j} = f_j(\mathbf{ z}_{i, :}), \] where \(\mathbf{ z}_{i, :}\) is the \(i\)th row of the latent variables, \(\mathbf{Z}\), then show that \[ f_j(\mathbf{ z}_{i, :}) = \mathbf{ w}_{j, :}^\top \mathbf{ z}_{i, :} \]

Latent Variables vs Linear Regression

The difference between this model and a multiple output regression is that in the regression case we are provided with the covariates \(\mathbf{Z}\), here they are latent variables. These variables are unknown. Just as we have done in the past for unknowns, we now treat them with a probability distribution. In factor analysis we assume that the latent variables have a Gaussian density which is independent across both across the latent variables associated with the different data points, and across those associated with different data features, so we have, \[ x_{i,j} \sim \mathcal{N}\left(0,1\right), \] and we can write the density governing the latent variable associated with a single point as, \[ \mathbf{ z}_{i, :} \sim \mathcal{N}\left(\mathbf{0},\mathbf{I}\right). \] If we consider the values of the function for the \(i\)th data point as \[ \mathbf{f}_{i, :} = \mathbf{f}(\mathbf{ z}_{i, :}) = \mathbf{W}\mathbf{ z}_{i, :} \] then we can use the rules for multivariate Gaussian relationships to write that \[ \mathbf{f}_{i, :} \sim \mathcal{N}\left(\mathbf{0},\mathbf{W}\mathbf{W}^\top\right) \] which implies that the distribution for \(\mathbf{ y}_{i, :}\) is given by \[ \mathbf{ y}_{i, :} = \sim \mathcal{N}\left(\mathbf{0},\mathbf{W}\mathbf{W}^\top + \boldsymbol{\Sigma}\right) \] where \(\boldsymbol{\Sigma}\) the covariance of the noise variable, \(\epsilon_{i, :}\) which for factor analysis is a diagonal matrix (because we have assumed that the noise was independent across the features), \[ \boldsymbol{\Sigma} = \begin{bmatrix}\sigma^2_{1} & 0 & 0 & 0\\ 0 & \sigma^2_{2} & 0 & 0\\ 0 & 0 & \ddots & 0\\ 0 & 0 & 0 & \sigma^2_p\end{bmatrix}. \] For completeness, we could also add in a mean for the data vector \(\boldsymbol{ \mu}\), \[ \mathbf{ y}_{i, :} = \mathbf{W}\mathbf{ z}_{i, :} + \boldsymbol{ \mu}+ \boldsymbol{ \epsilon}_{i, :} \] which would give our marginal distribution for \(\mathbf{ y}_{i, :}\) a mean \(\boldsymbol{ \mu}\). However, the maximum likelihood solution for \(\boldsymbol{ \mu}\) turns out to equal the empirical mean of the data, \[ \boldsymbol{ \mu}= \frac{1}{n} \sum_{i=1}^n \mathbf{ y}_{i, :}, \] regardless of the form of the covariance, \(\mathbf{C}= \mathbf{W}\mathbf{W}^\top + \boldsymbol{\Sigma}\). As a result it is very common to simply preprocess the data and ensure it is zero mean. We will follow that convention for this session.

The prior density over latent variables is independent, and the likelihood is independent, that means that the marginal likelihood here is also independent over the data points. Factor analysis was developed mainly in psychology and the social sciences for understanding personality and intelligence. Charles Spearman was concerned with the measurements of “the abilities of man” and is credited with the earliest version of factor analysis.

Principal Component Analysis

In 1933 Harold Hotelling published on principal component analysis the first mention of this approach (Hotelling, 1933). Hotelling’s inspiration was to provide mathematical foundation for factor analysis methods that were by then widely used within psychology and the social sciences. His model was a factor analysis model, but he considered the noiseless ‘limit’ of the model. In other words he took \(\sigma^2_i \rightarrow 0\) so that he had

\[ \mathbf{ y}_{i, :} \sim \lim_{\sigma^2 \rightarrow 0} \mathcal{N}\left(\mathbf{0},\mathbf{W}\mathbf{W}^\top + \sigma^2 \mathbf{I}\right). \] The paper had two unfortunate effects. Firstly, the resulting model is no longer valid probablistically, because the covariance of this Gaussian is ‘degenerate’. Because \(\mathbf{W}\mathbf{W}^\top\) has rank of at most \(q\) where \(q<p\) (due to the dimensionality reduction) the determinant of the covariance is zero, meaning the inverse doesn’t exist so the density, \[ p(\mathbf{ y}_{i, :}|\mathbf{W}) = \lim_{\sigma^2 \rightarrow 0} \frac{1}{(2\pi)^\frac{p}{2} |\mathbf{W}\mathbf{W}^\top + \sigma^2 \mathbf{I}|^{\frac{1}{2}}} \exp\left(-\frac{1}{2}\mathbf{ y}_{i, :}\left[\mathbf{W}\mathbf{W}^\top+ \sigma^2 \mathbf{I}\right]^{-1}\mathbf{ y}_{i, :}\right), \] is not valid for \(q<p\) (where \(\mathbf{W}\in \Re^{p\times q}\)). This mathematical consequence is a probability density which has no ‘support’ in large regions of the space for \(\mathbf{ y}_{i, :}\). There are regions for which the probability of \(\mathbf{ y}_{i, :}\) is zero. These are any regions that lie off the hyperplane defined by mapping from \(\mathbf{ z}\) to \(\mathbf{ y}\) with the matrix \(\mathbf{W}\). In factor analysis the noise corruption, \(\boldsymbol{ \epsilon}\), allows for points to be found away from the hyperplane. In Hotelling’s PCA the noise variance is zero, so there is only support for points that fall precisely on the hyperplane. Secondly, Hotelling explicity chose to rename factor analysis as principal component analysis, arguing that the factors social scientist sought were different in nature to the concept of a mathematical factor. This was unfortunate because the factor loadings, \(\mathbf{W}\) can also be seen as factors in the mathematical sense because the model Hotelling defined is a Gaussian model with covariance given by \(\mathbf{C}= \mathbf{W}\mathbf{W}^\top\) so \(\mathbf{W}\) is a factor of the covariance in the mathematical sense, as well as a factor loading.

However, the paper had one great advantage over standard approaches to factor analysis. Despite the fact that the model was a special case that is subsumed by the more general approach of factor analysis it is this special case that leads to a particular algorithm, namely that the factor loadings (or principal components as Hotelling referred to them) are given by an eigenvalue decomposition of the empirical covariance matrix.

Computation of the Marginal Likelihood

\[ \mathbf{ y}_{i,:}=\mathbf{W}\mathbf{ z}_{i,:}+\boldsymbol{ \epsilon}_{i,:},\quad \mathbf{ z}_{i,:} \sim \mathcal{N}\left(\mathbf{0},\mathbf{I}\right), \quad \boldsymbol{ \epsilon}_{i,:} \sim \mathcal{N}\left(\mathbf{0},\sigma^{2}\mathbf{I}\right) \]

\[ \mathbf{W}\mathbf{ z}_{i,:} \sim \mathcal{N}\left(\mathbf{0},\mathbf{W}\mathbf{W}^\top\right) \]

\[ \mathbf{W}\mathbf{ z}_{i, :} + \boldsymbol{ \epsilon}_{i, :} \sim \mathcal{N}\left(\mathbf{0},\mathbf{W}\mathbf{W}^\top + \sigma^2 \mathbf{I}\right) \]

Probabilistic PCA Max. Likelihood Soln (Tipping and Bishop (1999))

Figure: Graphical model representing probabilistic PCA.

\[p\left(\mathbf{Y}|\mathbf{W}\right)=\prod_{i=1}^{n}\mathcal{N}\left(\mathbf{ y}_{i, :}|\mathbf{0},\mathbf{W}\mathbf{W}^{\top}+\sigma^{2}\mathbf{I}\right)\]

Eigenvalue Decomposition

Eigenvalue problems are widespreads in physics and mathematics, they are often written as a matrix/vector equation but we prefer to write them as a full matrix equation. In an eigenvalue problem you are looking to find a matrix of eigenvectors, \(\mathbf{U}\) and a diagonal matrix of eigenvalues, \(\boldsymbol{\Lambda}\) that satisfy the matrix equation \[ \mathbf{A}\mathbf{U} = \mathbf{U}\boldsymbol{\Lambda}. \] where \(\mathbf{A}\) is your matrix of interest. This equation is not trivially solvable through matrix inverse because matrix multiplication is not commutative, so premultiplying by \(\mathbf{U}^{-1}\) gives \[ \mathbf{U}^{-1}\mathbf{A}\mathbf{U} = \boldsymbol{\Lambda}, \] where we remember that \(\boldsymbol{\Lambda}\) is a diagonal matrix, so the eigenvectors can be used to diagonalise the matrix. When performing the eigendecomposition on a Gaussian covariances, diagonalisation is very important because it returns the covariance to a form where there is no correlation between points.

Positive Definite

We are interested in the case where \(\mathbf{A}\) is a covariance matrix, which implies it is positive definite. A positive definite matrix is one for which the inner product, \[ \mathbf{ w}^\top \mathbf{C}\mathbf{ w} \] is positive for all values of the vector \(\mathbf{ w}\) other than the zero vector. One way of creating a positive definite matrix is to assume that the symmetric and positive definite matrix \(\mathbf{C}\in \Re^{p\times p}\) is factorised into, \(\mathbf{A}in \Re^{p\times p}\), a full rank matrix, so that \[ \mathbf{C}= \mathbf{A}^\top \mathbf{A}. \] This ensures that \(\mathbf{C}\) must be positive definite because \[ \mathbf{ w}^\top \mathbf{C}\mathbf{ w}=\mathbf{ w}^\top \mathbf{A}^\top\mathbf{A}\mathbf{ w} \] and if we now define a new vector \(\mathbf{b}\) as \[ \mathbf{b} = \mathbf{A}\mathbf{ w} \] we can now rewrite as \[ \mathbf{ w}^\top \mathbf{C}\mathbf{ w}= \mathbf{b}^\top\mathbf{b} = \sum_{i} b_i^2 \] which, since it is a sum of squares, is positive or zero. The constraint that \(\mathbf{A}\) must be full rank ensures that there is no vector \(\mathbf{ w}\), other than the zero vector, which causes the vector \(\mathbf{b}\) to be all zeros.

Exercise 3

If \(\mathbf{C}=\mathbf{A}^\top \mathbf{A}\) then express \(c_{i,j}\), the value of the element at the \(i\)th row and the \(j\)th column of \(\mathbf{C}\), in terms of the columns of \(\mathbf{A}\). Use this to show that (i) the matrix is symmetric and (ii) the matrix has positive elements along its diagonal.

Eigenvectors of a Symmetric Matric

Symmetric matrices have orthonormal eigenvectors. This means that \(\mathbf{U}\) is an orthogonal matrix, \(\mathbf{U}^\top\mathbf{U} = \mathbf{I}\). This implies that \(\mathbf{u}_{:, i} ^\top \mathbf{u}_{:, j}\) is equal to 0 if \(i\neq j\) and 1 if \(i=j\).

Thanks!

For more information on these subjects and more you might want to check the following resources.

• book: The Atomic Human
• twitter: @lawrennd
• podcast: The Talking Machines
• newspaper: Guardian Profile Page
• blog: http://inverseprobability.com

References