Sensitivity Analysis

Emukit Sensitivity Analysis

A possible definition of sensitivity analysis is the following: The study of how uncertainty in the output of a model (numerical or otherwise) can be apportioned to different sources of uncertainty in the model input (Saltelli et al., 2004). A related practice is ‘uncertainty analysis’, which focuses rather on quantifying uncertainty in model output. Ideally, uncertainty and sensitivity analyses should be run in tandem, with uncertainty analysis preceding in current practice.

In Chapter 1 of Saltelli et al. (2008)

What is Sensitivity Analysis?

• Study of how output uncertainty relates to input uncertainty
• Determines which inputs contribute most to output variations
• Complements uncertainty analysis which quantifies output uncertainty
• Best practice: Run uncertainty analysis first, then sensitivity analysis

Local Sensitivity Analysis

• Examines function sensitivity around a specific point
• Uses partial derivatives (Jacobian matrix)
• Only valid near operating point
• Limited view - doesn’t capture global behavior
• Useful for small perturbations around operating point

Global Sensitivity Analysis

• Examines sensitivity across entire input domain
• Uses ANOVA/Hoeffding-Sobol decomposition
• Based on total variance of function
• Requires assumptions about input distributions
• More comprehensive than local analysis

The Maths

• Total variance of function: \[\text{var}\left(g(\mathbf{ x})\right) = \left\langle g(\mathbf{ x})^2 \right\rangle _{p(\mathbf{ x})} - \left\langle g(\mathbf{ x}) \right\rangle _{p(\mathbf{ x})}^2\]

• Expectation defined as: \[\left\langle h(\mathbf{ x}) \right\rangle _{p(\mathbf{ x})} = \int_\mathbf{ x}h(\mathbf{ x}) p(\mathbf{ x}) \text{d}\mathbf{ x}\]

• \(p(\mathbf{ x})\) represents probability distribution of inputs

Input Density

• Assume inputs are independent
• Each input uniformly distributed
• Scale inputs to [0,1] interval
• Simplifies analysis while maintaining generality

Input Density Mathematics

• Independent inputs means: \[p(\mathbf{ x}) = \prod_{i=1}^pp(x_i)\]
• Uniform distribution on [0,1]: \[x_i \sim \mathcal{U}\left(0,1\right)\]

Hoeffding-Sobol Decomposition

Decomposition

• Function decomposed into sum of terms: \[g(\mathbf{ x}) = g_0 + \sum_{i=1}^pg_i(x_i) + \sum_{i<j}^{p} g_{ij}(x_i,x_j)\] \[+ \sum_{i<j<k}^{p} g_{ijk}(x_i,x_j,x_k) + \cdots + g_{1,2,\dots,p}(x_1,\dots,x_p)\]

Decomposition Terms

• Terms represent:
  • Constant (\(g_0\))
  • Individual effects (\(g_i\))
  • Interaction effects (\(g_{ij}\))
  • Higher-order interactions

Base Terms

• Constant term is overall expectation: \[g_0 = \left\langle g(\mathbf{ x}) \right\rangle _{p(\mathbf{ x})}\]
• Individual effects: \[g_i(x_i) = \left\langle g(\mathbf{ x}) \right\rangle _{p(\mathbf{ x}_{\sim i})} - g_0\]
• Where \(p(\mathbf{ x}_{\sim i})\) means marginalizing out \(i\)th variable: \[p(\mathbf{ x}_{\sim i}) = \int p(\mathbf{ x}) \text{d}x_i\]

Interaction Terms

• Two-way interactions: \[g_{i,j}(x_i, x_j) = \left\langle g(\mathbf{ x}) \right\rangle _{p(\mathbf{ x}_{\sim i,j})} - g_i - g_j - g_0\]
• Higher order terms follow similar pattern
• Each term requires computing lower-order terms first

{The Hoeffding-Sobol, or ANOVA, decomposition of a function allows us to write it as, \[ \begin{align*} g(\mathbf{ x}) = & g_0 + \sum_{i=1}^pg_i(x_i) + \sum_{i<j}^{p} g_{ij}(x_i,x_j) + \cdots \\ & + g_{1,2,\dots,p}(x_1,x_2,\dots,x_p), \end{align*} \] where \[ g_0 = \expectationDist{g(\mathbf{ x})}{p(\mathbf{ x}) \] and \[ g_i(x_i) = \left\langle g(\mathbf{ x}) \right\rangle _{p(\mathbf{ x}_{\sim i})} - g_0, \] where we’re using the notation \(p(\mathbf{ x}_{\sim i})\) to represent the input distribution with the \(i\)th variable marginalised, \[ p(\mathbf{ x}_{\sim i}) = \int p(\mathbf{ x}) \text{d}x_i \] Higher order terms in the decomposition represent interactions between inputs, \[ g_{i,j}(x_i, x_j) = \left\langle g(\mathbf{ x}) \right\rangle _{p(\mathbf{ x}_{\sim i,j})} - g_i(x_i) - g_j(x_j) - g_0 \] and similar expressions can be written for higher order terms up to \(g_{1,2,\dots,p}(\mathbf{ x})\).}

Variance Decomposition

• Sobol decomposition components are orthogonal
• Leads to variance decomposition: \[\text{var}(g) = \left\langle g(\mathbf{ x})^2 \right\rangle _{p(\mathbf{ x})} - g_0^2\]

ANOVA Decomposition

• Decomposes into sum of variance terms: \[\text{var}(g) = \sum_{i=1}^p\text{var}\left(g_i(x_i)\right) + \sum_{i<j}^{p} \text{var}\left(g_{ij}(x_i,x_j)\right) + \cdots\]
• Known as ANOVA (Analysis of Variance) decomposition
• Each term represents variance from different input interactions

Sobol Indices

• Rescale variance components by total variance
• Gives Sobol indices: \[S_\ell = \frac{\text{var}\left(g(\mathbf{ x}_\ell)\right)}{\text{var}\left(g(\mathbf{ x})\right)}\]
• \(\ell\) represents different input combinations
• See Durrande et al. (2013) for elegant approach using covariance structure

Sobol Indices: The Intuition

• Sobol indices tell us “how much each input matters”
• Values between 0 and 1:
  • 0 means input has no effect
  • 1 means output variance entirely due to this input
• Can analyze:
  • Individual inputs (\(S_i\))
  • Pairs of inputs (\(S_{ij}\))
  • Higher-order interactions
• Sum of all indices = 1

Example: the Ishigami function

Ishigami Function Example: Overview

• Will explore sensitivity analysis using Ishigami test function
• Selected because it allows exact calculation of Sobol indices
• In real applications, exact calculation rarely possible
• Will demonstrate progression of methods:
  1. Exact calculation (possible for Ishigami)
  2. Monte Carlo estimation (general but expensive)
  3. GP emulation (efficient approximation)

Ishigami Function

\[ g(\textbf{x}) = \sin(x_1) + a \sin^2(x_2) + b x_3^4 \sin(x_1). \]

Total Variance

First Order Sobol Indices using Monte Carlo

\[ S_i = \frac{\text{var}\left(g_i(x_i)\right)}{\text{var}\left(g(\mathbf{ x})\right)}. \]

• First plot compares true Sobol indices with Monte Carlo estimates
• Shows relative importance of each input variable
• Demonstrates accuracy of Monte Carlo sampling approach

Total Effects Using Monte Carlo

• Next plot shows total effects - including all variable interactions
• Compares true values with Monte Carlo estimates
• Demonstrates how variables influence output through interactions

Computing the Sensitivity Indices Using the Output of a Model

• Final plots compare three approaches:
  • True Sobol indices
  • Direct Monte Carlo estimation
  • GP-based estimation
• Shows how GP emulator can approximate sensitivity with fewer samples

Conclusions

• Sobol indices tool for explaining variance of output as coponents of input variables.

Catapult Simulation

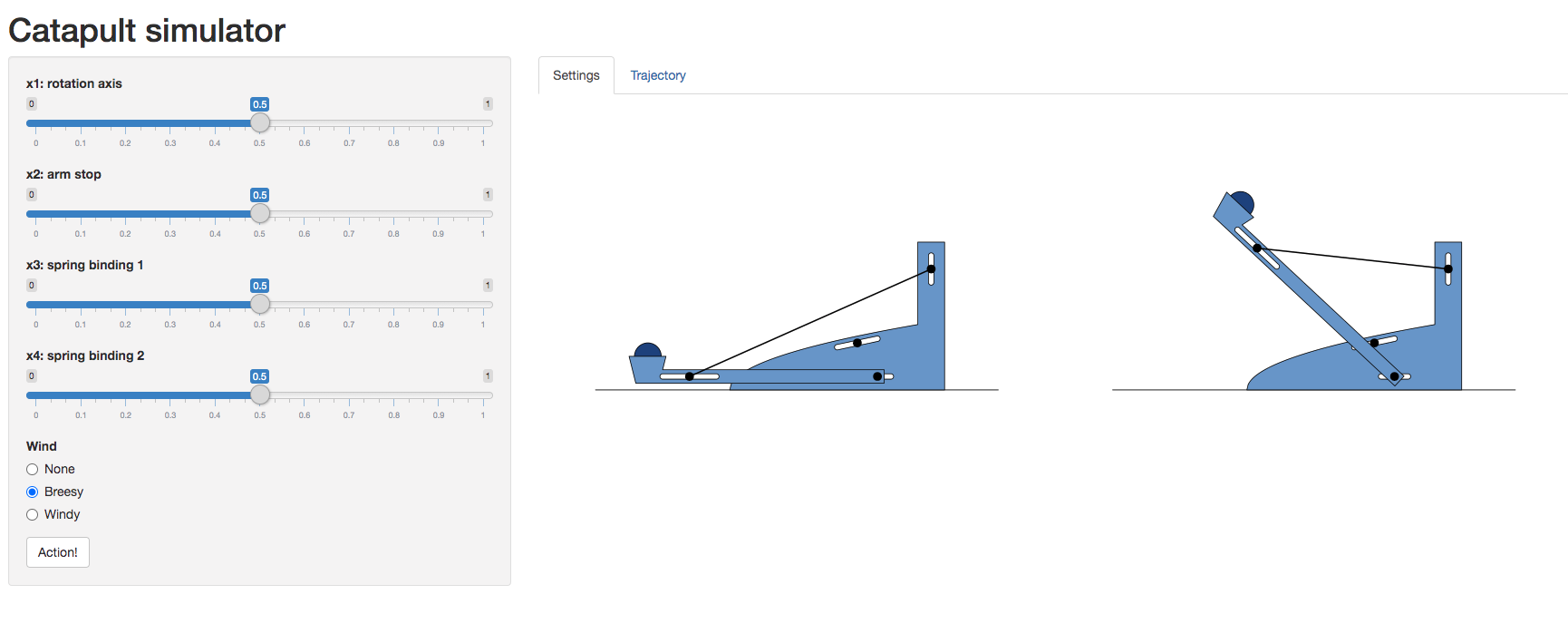
Catapult Parameters

• Four key parameters control the catapult:
  • rotation_axis: Axis the arm rotates around
  • arm_stop: Position where arm stops
  • spring_binding_1: First spring attachment point
    
  • spring_binding_2: Second spring attachment point

Parameter Vector

• Parameters combined into vector:

\[ \mathbf{ x}_i = \begin{bmatrix} \texttt{rotation_axis} \\ \texttt{arm_stop} \\ \texttt{spring_binding_1} \\ \texttt{spring_binding_2} \end{bmatrix} \]

Running Experiments

• Fire catapult with chosen parameters
• Record distance traveled
• Helper function requests distance for each configuration

Parameter Space

• All parameters scaled to [0,1] range
• Define continuous parameter space for optimization

Experimental Design for the Catapult

• First build an experimental design loop
• Start with model-free design (random, Latin hypercube, Sobol, orthogonal)
• Initialize with 5 random samples
• Build Gaussian process model
• Use model to guide further sampling

Model Based Design

• Two sampling strategies:
• Integrated variance reduction (minimize overall uncertainty)
• Uncertainty sampling (sample highest variance points)
• Trade-off between accuracy and computation speed

Sensitivity Analysis of a Catapult Simulation

• We’ll use Monte Carlo sensitivity analysis to understand which parameters matter most
• This helps us identify which parameters we should focus on when optimizing the catapult
• We’ll use our GP emulator to efficiently estimate Sobol indices
• Two types of indices:
  • First order - direct influence of each parameter
  • Total effects - includes parameter interactions

First Order Sobol Indices

• First order Sobol indices show direct parameter effects
• Higher percentage = parameter has stronger direct influence on catapult distance
• Helps identify which parameters to prioritize for optimization

First Order Sobol Indices

Total Effects Sobol Indices

• Total effects include both direct influence and parameter interactions
• Larger difference between total and first order effects indicates strong parameter interactions
• Understanding interactions helps with joint parameter optimization

Total Effects Sobol Indices