Introduction: ML and the Physical World

Neil D. Lawrence

Course Overview

  • Week 1:
    1. Introduction. Lecturer: Neil D. Lawrence
    2. Quantification of Beliefs. Lecturer: Carl Henrik Ek
  • Week 2:
    1. Gaussian processes. Lecturer: Carl Henrik Ek
    2. Simulation. Lecturer: Neil D. Lawrence

Course Overview

  • Week 3:
    1. Emulation. Lecturer: Neil D. Lawrence
    2. Sequential Decision Making Under Uncertainty: Bayesian Inference. Lecturer: Carl Henrik Ek
  • Week 4:
    1. Probabilistic Numerics. Lecturer: Carl Henrik Ek
    2. Emukit and Experimental Design. Lecturer: Neil D. Lawrence

Course Overview

  • Week 5:
    1. Sensitivity Analysis. Lecturer: Neil D. Lawrence
    2. Multifidelity Modelling. Lecturer: Neil D. Lawrence

Special Topics

  • Weeks 6-8 will involve three special topics.
  • In 2020 we had:
    • Simulation in the Covid-19 Pandemic (Andrei Paleyes, Cambridge and DELVE)
    • Climate Modelling (Scott Hoskins, BAS)
    • Simulation and Personalized Medicine (Javier Gonzalez, Microsoft Research)

Special Topics

  • Weeks 6-8 will involve three special topics.
  • In 2021 we had:
    • Spectroscopy data (Marie Synakewicz, Zurich)
    • Amazon Supply Chain (Jordan Bell-Masterson, Amazon)
    • Climate Science (Scott Hoskins, BAS)
    • Elasticity Data (Tim Dodwell, Exeter)

Assessment

  • Lab sheet for completion by end of Week 5.
  • Mini projects starting in Week 6 in small groups deploying lessons you’ve learnt

Course Material

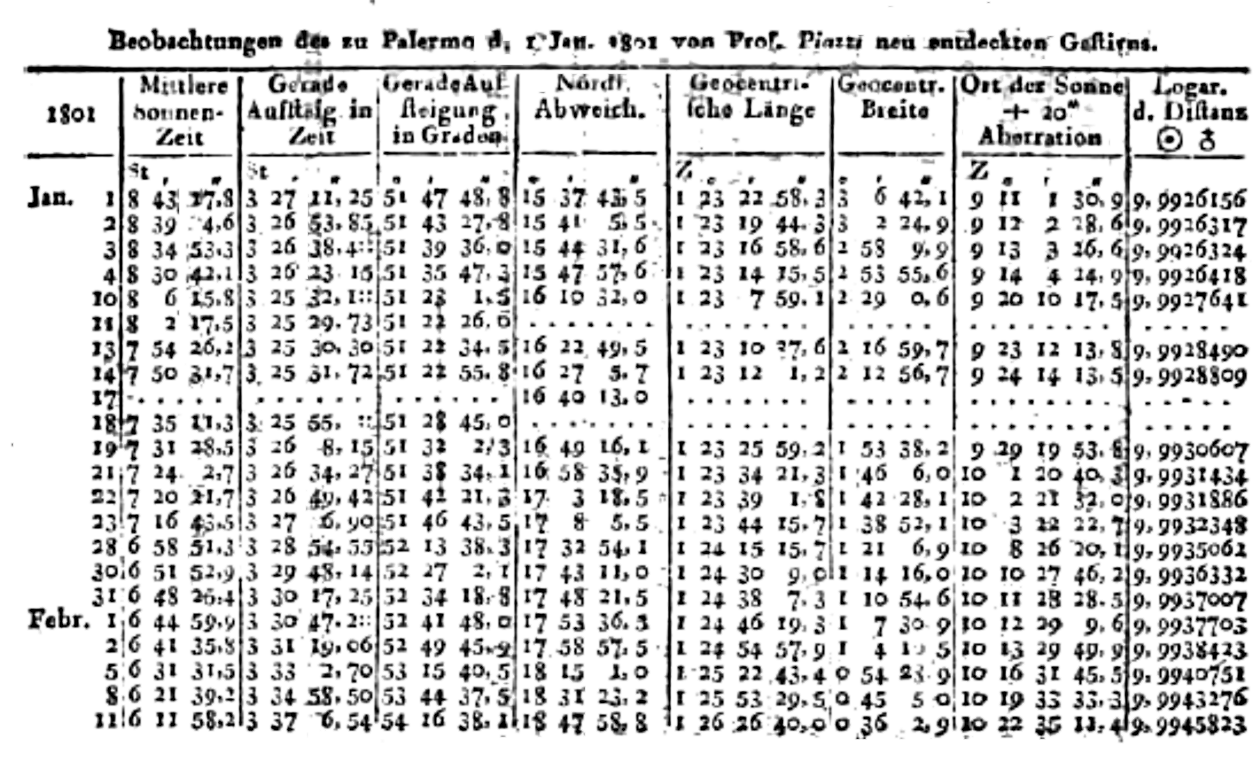
Titius-Bode Law

Overdetermined System

\(y= mx+ c\)

point 1: \(x= 1\), \(y=3\) \[ 3 = m + c \]

point 2: \(x= 3\), \(y=1\) \[ 1 = 3m + c \]

point 3: \(x= 2\), \(y=2.5\) \[ 2.5 = 2m + c \]

Pierre-Simon Laplace

Laplace’s Demon

Laplace’s Demon

Philosophical Essay on Probabilities Laplace (1814) pg 3

Machine Learning

\[ \text{model} + \text{data} \stackrel{\text{compute}}{\rightarrow} \text{prediction}\]

Theory of Everything

If we do discover a theory of everything … it would be the ultimate triumph of human reason-for then we would truly know the mind of God

Stephen Hawking in A Brief History of Time 1988

Laplace’s Gremlin

Philosophical Essay on Probabilities Laplace (1814) pg 5

\(y= mx+ c + \epsilon\)

point 1: \(x= 1\), \(y=3\) \[ 3 = m + c + \epsilon_1 \]

point 2: \(x= 3\), \(y=1\) \[ 1 = 3m + c + \epsilon_2 \]

point 3: \(x= 2\), \(y=2.5\) \[ 2.5 = 2m + c + \epsilon_3 \]

A Probabilistic Process

Set the mean of Gaussian to be a function. \[ p\left(y_i|x_i\right)=\frac{1}{\sqrt{2\pi\sigma^2}}\exp \left(-\frac{\left(y_i-f\left(x_i\right)\right)^{2}}{2\sigma^2}\right). \]

This gives us a ‘noisy function’.

This is known as a stochastic process.

Hydrodynamica

Entropy Billiards

Entropy:

Underdetermined System

Underdetermined System

  • What about two unknowns and one observation? \[y_1 = mx_1 + c\]

Can compute \(m\) given \(c\). \[m = \frac{y_1 - c}{x}\]

Underdetermined System

Brownian Motion and Wiener

Betrand Russell
Albert Einstein
Norbert Wiener

Brownian Motion

Stochasticity and Control

Conclusions

  • Potted journey through history of physical models and uncertainty.
  • Challenge we now face is partial uncertainty.
  • This module will equip you with the skills to balance uncertainty, computation and observation in answering scientific questions.

Thanks!

References

Boltzmann, L., n.d. Über die Beziehung zwischen dem zweiten Hauptsatze der mechanischen Warmetheorie und der Wahrscheinlichkeitsrechnung, respective den Sätzen über das wärmegleichgewicht. Sitzungberichte der Kaiserlichen Akademie der Wissenschaften. Mathematisch-Naturwissen Classe. Abt. II LXXVI, 373–435.
Coales, J.F., Kane, S.J., 2014. The “yellow peril” and after. IEEE Control Systems Magazine 34, 65–69. https://doi.org/10.1109/MCS.2013.2287387
Eddington, A.S., 1929. The nature of the physical world. Dent (London). https://doi.org/10.2307/2180099
Einstein, A., 1905. Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen. Annalen der Physik 322, 549–560. https://doi.org/10.1002/andp.19053220806
Laplace, P.S., 1814. Essai philosophique sur les probabilités, 2nd ed. Courcier, Paris.
Mikhailov, G.K., n.d. Daniel bernoulli, hydrodynamica (1738).
Sharp, K., Matschinsky, F., 2015. Translation of Ludwig Boltzmann’s paper “on the relationship between the second fundamental theorem of the mechanical theory of heat and probability calculations regarding the conditions for thermal equilibrium.” Entropy 17, 1971–2009. https://doi.org/10.3390/e17041971