Deep Architectures

Review

• Advanced Data Science
• ML and the Physical World
• Deep Neural Networks

Basis Functions to Neural Networks

From Basis Functions to Neural Networks

• So far: linear models or “shallow learning”
• Consider instead function composition or “deep learning”

Neural Network Prediction Function

\[ f(\mathbf{ x}; \mathbf{W}) = \mathbf{ w}_4 ^\top\phi\left(\mathbf{W}_3 \phi\left(\mathbf{W}_2\phi\left(\mathbf{W}_1 \mathbf{ x}\right)\right)\right). \]

Linear Models as Basis + Weights

\[ f(\mathbf{ x}_i) = \mathbf{ w}^\top \boldsymbol{ \phi}(\mathbf{ x}_i). \]

Deep Neural Network

Deep Neural Network

Mathematically

\[ \begin{align*} \mathbf{ h}_{1} &= \phi\left(\mathbf{W}_1 \mathbf{ x}\right)\\ \mathbf{ h}_{2} &= \phi\left(\mathbf{W}_2\mathbf{ h}_{1}\right)\\ \mathbf{ h}_{3} &= \phi\left(\mathbf{W}_3 \mathbf{ h}_{2}\right)\\ f&= \mathbf{ w}_4 ^\top\mathbf{ h}_{3} \end{align*} \]

From Shallow to Deep

\[ f(\mathbf{ x}; \mathbf{W}) = \mathbf{ w}_4 ^\top\phi\left(\mathbf{W}_3 \phi\left(\mathbf{W}_2\phi\left(\mathbf{W}_1 \mathbf{ x}\right)\right)\right). \]

Gradient-based optimization

\[ E(\mathbf{W}) = \sum_{i=1}^nE(\mathbf{ y}_i, f(\mathbf{ x}_i; \mathbf{W})) \]

\[ \mathbf{W}_{t+1} = \mathbf{W}_t - \eta \nabla_\mathbf{W}E(\mathbf{W}) \]

Basic Multilayer Perceptron

\[ \small f_L(\mathbf{ x}) = \boldsymbol{ \phi}\left(\mathbf{b}_L+ \mathbf{W}_L\boldsymbol{ \phi}\left(\mathbf{b}_{L-1} + \mathbf{W}_{L-1} \boldsymbol{ \phi}\left( \cdots \boldsymbol{ \phi}\left(\mathbf{b}_1 + \mathbf{W}_1 \mathbf{ x}\right) \cdots \right)\right)\right) \]

Recursive MLP Definition

\[\begin{align} f_\ell(\mathbf{ x}) &= \boldsymbol{ \phi}\left(\mathbf{W}_\ell f_{\ell-1}(\mathbf{ x}) + \mathbf{b}_\ell\right),\quad l=1,\dots,L\\ f_0(\mathbf{ x}) &= \mathbf{ x} \end{align}\]

Rectified Linear Unit

Shallow ReLU Networks

\[\begin{align} \mathbf{h}(x) &= \operatorname{ReLU}(\mathbf{w}_1 x - \mathbf{b}_1)\\ f(x) &= \mathbf{w}_2^{\top} \, \mathbf{h}(x) \end{align}\]

ReLU Activations

Decision Boundaries

Decision Boundaries

Complexity (1D): number of kinks \(\propto\) width of network.

Depth vs Width: Representation Power

• Single hidden layer: number of kinks \(\approx O(\text{width})\)
• Deep ReLU networks: kinks \(\approx O(2^{\text{depth}})\)

Sawtooth Construction

\[\begin{align} f_l(x) &= 2\vert f_{l-1}(x)\vert - 2, \quad f_0(x) = x\\ f_l(x) &= 2 \operatorname{ReLU}(f_{l-1}(x)) + 2 \operatorname{ReLU}(-f_{l-1}(x)) - 2 \end{align}\]

Complexity (1D): number of kinks \(\approx O(2^{\text{depth}})\).

Higher-dimensional Geometry

• Regions: piecewise-linear, often triangular/polygonal in 2D
• Continuity arises despite stitching flat regions
• Early layers: few regions; later layers: many more

Chain Rule and Back Propgation

Historical Context

• 1957: Rosenblatt’s Perceptron with multiple layers
• Association units: deep structure with random weights
• Modern approach: adjust weights to minimise error

Parameterised Basis Functions

• Basis functions: \(\boldsymbol{ \phi}(\mathbf{ x}; \mathbf{V})\)
• Adjustable parameters: \(\mathbf{V}\) can be optimized
• Non-linear models: in both inputs and parameters

The Gradient Problem

• Model: \(f(\mathbf{ x}_i) = \mathbf{ w}^\top \boldsymbol{ \phi}(\mathbf{ x}_i; \mathbf{V})\)
• Easy gradient: \(\frac{\text{d}f_i}{\text{d}\mathbf{ w}} = \boldsymbol{ \phi}(\mathbf{ x}_i; \mathbf{V})\)
• Hard gradient: \(\frac{\text{d}f_i}{\text{d}\mathbf{V}}\)

Chain Rule Application

\[\frac{\text{d}f_i}{\text{d}\mathbf{V}} = \frac{\text{d}f_i}{\text{d}\boldsymbol{ \phi}_i}\frac{\text{d}\boldsymbol{ \phi}_i}{\text{d} \mathbf{V}}\]

The Matrix Challenge

• Chain rule: standard approach
• New challenge: \(\frac{\text{d}\boldsymbol{ \phi}_i}{\text{d} \mathbf{V}}\)
• Problem: derivative of vector with respect to matrix

Matrix Vector Chain Rule

Matrix Calculus Standards

• Multiple approaches to multivariate chain rule
• Mike Brookes’ method: preferred approach
• Reference: Brookes (2005)

Brookes’ Approach

• Never compute matrix derivatives directly
• Stacking operation: intermediate step
• Vector derivatives: easier to handle

Matrix Stacking

• Input: matrix \(\mathbf{A}\)
• Output: vector \(\mathbf{a}\)
• Process: stack columns vertically

Stacking Formula

\[\mathbf{a} = \begin{bmatrix} \mathbf{a}_{:, 1}\\ \mathbf{a}_{:, 2}\\ \vdots\\ \mathbf{a}_{:, q} \end{bmatrix}\]

• Column stacking: each column becomes a block
• Order: first column at top, last at bottom
• Size: \(mn \times 1\) vector from \(m \times n\) matrix

Vector Derivatives

\[\frac{\text{d} \mathbf{a}}{\text{d} \mathbf{b}} \in \Re^{m \times n}\]

• Input: \(\mathbf{a} \in \Re^{m \times 1}\), \(\mathbf{b} \in \Re^{n \times 1}\)
• Output: \(m \times n\) matrix
• Standard form: vector-to-vector derivatives

Matrix Stacking Notation

• \(\mathbf{C}\!:\) vector formed from matrix \(\mathbf{C}\)
• Stacking: columns of \(\mathbf{C}\) → \(\Re^{mn \times 1}\) vector
• Condition: \(\mathbf{C} \in \Re^{m \times n}\)

Matrix-Matrix Derivatives

\[\frac{\text{d} \mathbf{E}}{\text{d} \mathbf{C}} \in \Re^{pq \times mn}\]

• Input: \(\mathbf{E} \in \Re^{p \times q}\), \(\mathbf{C} \in \Re^{m \times n}\)
• Output: \(pq \times mn\) matrix
• Advantage: easier chain rule application

Kronecker Products

• Notation: \(\mathbf{F} \otimes \mathbf{G}\)
• Essential tool: for matrix derivatives
• Key role: in chain rule applications

Kronecker Products

• Notation: \(\mathbf{A} \otimes \mathbf{B}\)
• Input: matrices \(\mathbf{A} \in \Re^{m \times n}\), \(\mathbf{B} \in \Re^{p \times q}\)
• Output: \((mp) \times (nq)\) matrix

Visual Examples

Kronecker Product Visualization

Column vs Row Stacking

• Column stacking: \(\mathbf{I} \otimes \mathbf{K}\) - time independence
• Row stacking: \(\mathbf{K} \otimes \mathbf{I}\) - dimension independence
  
• Different structure: affects which variables are correlated

Kronecker Product Formula

\[(\mathbf{A} \otimes \mathbf{B})_{ij} = a_{i_1 j_1} b_{i_2 j_2}\]

• Index mapping: \(i = (i_1-1)p + i_2\), \(j = (j_1-1)q + j_2\)
• Block structure: each element of \(\mathbf{A}\) scaled by \(\mathbf{B}\)
• Size: \((mp) \times (nq)\) result

Basic Properties

• Distributive: \((\mathbf{A} + \mathbf{B}) \otimes \mathbf{C} = \mathbf{A} \otimes \mathbf{C} + \mathbf{B} \otimes \mathbf{C}\)
• Associative: \((\mathbf{A} \otimes \mathbf{B}) \otimes \mathbf{C} = \mathbf{A} \otimes (\mathbf{B} \otimes \mathbf{C})\)
• Mixed product: \((\mathbf{A} \otimes \mathbf{B})(\mathbf{C} \otimes \mathbf{D}) = \mathbf{A}\mathbf{C} \otimes \mathbf{B}\mathbf{D}\)

Identity and Zero

• Identity: \(\mathbf{I}_m \otimes \mathbf{I}_n = \mathbf{I}_{mn}\)
• Zero: \(\mathbf{0} \otimes \mathbf{A} = \mathbf{A} \otimes \mathbf{0} = \mathbf{0}\)
• Scalar: \(c \otimes \mathbf{A} = \mathbf{A} \otimes c = c\mathbf{A}\)

Transpose and Inverse

• Transpose: \((\mathbf{A} \otimes \mathbf{B})^\top = \mathbf{A}^\top \otimes \mathbf{B}^\top\)
• Inverse: \((\mathbf{A} \otimes \mathbf{B})^{-1} = \mathbf{A}^{-1} \otimes \mathbf{B}^{-1}\) (when both exist)
• Determinant: \(\det(\mathbf{A} \otimes \mathbf{B}) = \det(\mathbf{A})^q \det(\mathbf{B})^m\)

Matrix Stacking and Kronecker Products

Column Stacking

• Stacking: place columns of matrix on top of each other
• Notation: \(\mathbf{a} = \text{vec}(\mathbf{A})\) or \(\mathbf{a} = \mathbf{A}\!:\)
• Kronecker form: \(\mathbf{I} \otimes \mathbf{K}\) for column-wise structure

Row Stacking

• Alternative: stack rows instead of columns
• Kronecker form: \(\mathbf{K} \otimes \mathbf{I}\) for row-wise structure
• Different structure: changes which variables are independent

Computational Advantages

Efficient Matrix Operations

• Inversion: \((\mathbf{A} \otimes \mathbf{B})^{-1} = \mathbf{A}^{-1} \otimes \mathbf{B}^{-1}\)
• Eigenvalues: \(\lambda_i(\mathbf{A} \otimes \mathbf{B}) = \lambda_j(\mathbf{A}) \lambda_k(\mathbf{B})\)
• Determinant: \(\det(\mathbf{A} \otimes \mathbf{B}) = \det(\mathbf{A})^q \det(\mathbf{B})^m\)

Memory and Speed Benefits

• Storage: avoid storing full covariance matrix
• Operations: work with smaller component matrices
• Scaling: \(O(n^3)\) becomes \(O(n_1^3 + n_2^3)\) for \(n = n_1 n_2\)

Kronecker Product Simplification

\[(\mathbf{E}:)^{\top} \mathbf{F} \otimes \mathbf{G}=\left(\left(\mathbf{G}^{\top} \mathbf{E F}\right):\right)^{\top}\]

• Removal rule: Kronecker products often simplified
• Chain rule: typically produces this form
• Key insight: avoid direct Kronecker computation

Chain Rule Application

\[\frac{\text{d} E}{\text{d} \mathbf{H}:} \frac{\text{d} \mathbf{H}:}{\text{d} \mathbf{J}:}=\frac{\text{d} E}{\text{d} \mathbf{J}:}\]

\[\frac{\text{d}\mathbf{H}}{\text{d} \mathbf{J}} = \mathbf{F} \otimes \mathbf{G}\]

Kronecker Product Identities

\[\mathbf{F}^{\top} \otimes \mathbf{G}^{\top}=(\mathbf{F} \otimes \mathbf{G})^{\top}\]

\[(\mathbf{E} \otimes \mathbf{G})(\mathbf{F} \otimes \mathbf{H})=\mathbf{E F} \otimes \mathbf{G H}\]

Derivative Representations

• Two forms: row vector vs matrix
• Row vector: easier computation
• Matrix: better summarization

\[\frac{\text{d} E}{\text{d} \mathbf{J}:}=\left(\left(\frac{\text{d} E}{\text{d} \mathbf{J}}\right):\right)^{\top}\]

Useful Multivariate Derivatives

Derivative of $mathbf{A} wrt \(\mathbf{A}\)

• Problem: \(\mathbf{b} = \mathbf{A}\mathbf{x}\), find \(\frac{\text{d}\mathbf{b}}{\text{d}\mathbf{A}}\)
• Approach: indirect derivation via \(\mathbf{a}^\prime\)
• Key insight: stacking rows vs columns

Indirect Approach

\[\frac{\text{d}}{\text{d} \mathbf{a^\prime}} \mathbf{A} \mathbf{x}\]

• Size: \(m \times mn\) matrix
• Definition: \(\mathbf{a}^\prime = \left(\mathbf{A}^\top\right):\)
• Stacking: columns of \(\mathbf{A}^\top\) = rows of \(\mathbf{A}\)

Row-wise Structure

\[\mathbf{A}\mathbf{x} = \begin{bmatrix} \mathbf{a}_{1, :}^\top \mathbf{x} \\ \mathbf{a}_{2, :}^\top \mathbf{x} \\ \vdots \\ \mathbf{a}_{m, :}^\top \mathbf{x} \end{bmatrix}\]

• Structure: inner products of rows of \(\mathbf{A}\)
• Gradient: \(\frac{\text{d}\mathbf{a}_{i,:}^\top \mathbf{x}}{\text{d}\mathbf{a}_{i,:}} = \mathbf{x}\)
• Expectation: repeated versions of \(\mathbf{x}\)

Kronecker Product Tiling

\[\mathbf{I}_m \otimes \mathbf{x}^\top = \begin{bmatrix} \mathbf{x}^\top & \mathbf{0}& \cdots & \mathbf{0}\\ \mathbf{0}& \mathbf{x}^\top & \cdots & \mathbf{0}\\ \vdots & \vdots & \ddots & \vdots \\ \mathbf{0}& \mathbf{0}& \cdots& \mathbf{x}^\top \end{bmatrix}\]

• Pattern: tiling of \(\mathbf{x}^\top\)
• Size: \(m \times nm\) matrix
• Structure: \(\mathbf{x}\) repeated in blocks

Final Result

\[\frac{\text{d}}{\text{d} \mathbf{a^\prime}} \mathbf{A} \mathbf{x} = \mathbf{I}_{m} \otimes \mathbf{x}^\top\]

• Each row: derivative of \(b_i = \mathbf{a}_{i, :}^\top \mathbf{x}\)
• Non-zero elements: only where \(\mathbf{a}_{i, :}\) appears
• Values: \(\mathbf{x}\) in appropriate positions

Column Stacking Alternative

\[\frac{\text{d}}{\text{d} \mathbf{a}} \mathbf{A} \mathbf{x} = \mathbf{x}^\top \otimes \mathbf{I}_{m}\]

• Change: \(\mathbf{a} = \mathbf{A}:\) (column stacking)
• Method: reverse Kronecker product order
• Result: \(\mathbf{x}^\top \otimes \mathbf{I}_{m}\)

Column Stacking Structure

\[\mathbf{x}^\top \otimes \mathbf{I}_{m} = \begin{bmatrix} x_1 \mathbf{I}_m & x_2 \mathbf{I}_m & \cdots & x_n \mathbf{I}_m \end{bmatrix}\]

• Pattern: \(\mathbf{x}\) elements distributed across blocks
• Size: \(m \times mn\) matrix
• Correct: for column stacking of \(\mathbf{A}\)

Chain Rule for Neural Networks

Neural Network Chain Rule

• Goal: compute gradients for neural networks
• Approach: apply matrix derivative rules
• Key: three fundamental gradients needed

Neural Network Structure

\[\mathbf{ f}_\ell= \mathbf{W}_\ell\boldsymbol{ \phi}_{\ell-1}\]

\[\boldsymbol{ \phi}_{\ell} = \boldsymbol{ \phi}_{\ell}(\mathbf{ f}_{\ell})\]

• Activations: \(\mathbf{ f}_\ell\) at layer \(\ell\)
• Basis functions: applied to activations
• Weight matrix: \(\mathbf{W}_\ell\)

First and Final Layers

\[f_1 = \mathbf{W}_1 \mathbf{ x}\]

\[\mathbf{h} = \mathbf{h}(\mathbf{ f}_L)\]

• First layer: \(f_1 = \mathbf{W}_1 \mathbf{ x}\)
• Final layer: inverse link function
• Dummy basis: \(\mathbf{h} = \boldsymbol{ \phi}_L\)

Limitations

• Skip connections: not captured in this formalism
• Example: layer \(\ell-2\) → layer \(\ell\)
• Sufficient: for main aspects of deep network gradients

Three Fundamental Gradients

• Activation gradient: \(\frac{\text{d}\mathbf{ f}_\ell}{\text{d}\mathbf{ w}_\ell}\)
• Basis gradient: \(\frac{\text{d}\boldsymbol{ \phi}_{\ell}}{\text{d} \mathbf{ f}_{\ell}}\)
• Across-layer gradient: \(\frac{\text{d}\mathbf{ f}_\ell}{\text{d}\boldsymbol{ \phi}_{\ell-1}}\)

Activation Gradient

\[\frac{\text{d}\mathbf{ f}_\ell}{\text{d}\mathbf{ w}_\ell} = \boldsymbol{ \phi}_{\ell-1}^\top \otimes \mathbf{I}_{d_\ell}\]

• Size: \(d_\ell\times (d_{\ell-1} d)\)
• Input: \(\mathbf{ f}_\ell\) and \(\mathbf{ w}_\ell\)
• Kronecker product: key to the result

Basis Gradient

\[\frac{\text{d}\boldsymbol{ \phi}_{\ell}}{\text{d} \mathbf{ f}_{\ell}} = \boldsymbol{ \Phi}^\prime\]

\[\frac{\text{d}\phi_i^{(\ell)}(\mathbf{ f}_{\ell})}{\text{d} f_j^{(\ell)}}\]

• Size: \(d_\ell\times d_\ell\) matrix
• Elements: derivatives of basis functions
• Diagonal: if basis functions depend only on their own activations

Activations and Gradients

Across-Layer Gradient

\[\frac{\text{d}\mathbf{ f}_\ell}{\text{d}\boldsymbol{ \phi}_{\ell-1}} = \mathbf{W}_\ell\]

• Size: \(d_\ell\times d_{\ell-1}\)
• Matches: shape of \(\mathbf{W}_\ell\)
• Simple: just the weight matrix itself

Complete Chain Rule

\[\frac{\text{d} \mathbf{ f}_\ell}{\text{d}\mathbf{ w}_{\ell-k}} = \left[\prod_{i=0}^{k-1} \frac{\text{d} \mathbf{ f}_{\ell - i}}{\text{d} \boldsymbol{ \phi}_{\ell - i -1}}\frac{\text{d} \boldsymbol{ \phi}_{\ell - i -1}}{\text{d} \mathbf{ f}_{\ell - i -1}}\right] \frac{\text{d} \mathbf{ f}_{\ell-k}}{\text{d} \mathbf{ w}_{\ell - k}}\]

• Product: of all intermediate gradients
• Chain: from layer \(\ell\) back to layer \(\ell-k\)
• Complete: gradient computation for any layer

Substituted Matrix Form

\[\frac{\text{d} \mathbf{ f}_\ell}{\text{d}\mathbf{ w}_{\ell-k}} = \left[\prod_{i=0}^{k-1} \mathbf{W}_{\ell - i} \boldsymbol{ \Phi}^\prime_{\ell - i -1}\right] \boldsymbol{ \phi}_{\ell-k-1}^\top \otimes \mathbf{I}_{d_{\ell-k}}\]

• Weight matrices: \(\mathbf{W}_{\ell - i}\) for across-layer gradients
• Basis derivatives: \(\boldsymbol{ \Phi}^\prime_{\ell - i -1}\) for activation derivatives
• Final term: Kronecker product for activation gradient

Gradient Verification

Verify Neural Network Gradients

Loss Functions

Test loss function gradients

Simple Deep NN Implementation

Create and Test Neural Network

Test Backpopagation

Unified Optimisation Interface

Train Network for Regression

mlai.write_figure(“nn-regression-training-progress.svg,” directory=“./ml”) }

{}{Neural Network Training Progress for a regression model.){nn-regression-training-progress}

Visualise Decision Boundary

Evaluating Derivatives

\[ \frac{\text{d} \mathbf{ f}_L}{\text{d} \mathbf{ w}} = \frac{\text{d} \mathbf{ f}_L}{\text{d} \mathbf{ f}_{L-1}} \frac{\text{d} \mathbf{ f}_{L-1}}{\text{d} \mathbf{ f}_{L-2}} \frac{\text{d} \mathbf{ f}_{L-2}}{\text{d} \mathbf{ f}_{L-3}} \cdots \frac{\text{d} \mathbf{ f}_3}{\text{d} \mathbf{ f}_{2}} \frac{\text{d} \mathbf{ f}_2}{\text{d} \mathbf{ f}_{1}} \frac{\text{d} \mathbf{ f}_1}{\text{d} \mathbf{ w}} \]

\[ \small \frac{\text{d} \mathbf{ f}_L}{\text{d} \mathbf{ w}} = \frac{\text{d} \mathbf{ f}_L}{\text{d} \mathbf{ f}_{L-1}} \left( \frac{\text{d} \mathbf{ f}_{L-1}}{\text{d} \mathbf{ f}_{L-2}} \left( \frac{\text{d} \mathbf{ f}_{L-2}}{\text{d} \mathbf{ f}_{L-3}} \cdots \left( \frac{\text{d} \mathbf{ f}_3}{\text{d} \mathbf{ f}_{2}} \left( \frac{\text{d} \mathbf{ f}_2}{\text{d} \mathbf{ f}_{1}} \frac{\text{d} \mathbf{ f}_1}{\text{d} \mathbf{ w}} \right) \right) \cdots \right) \right) \]

Or like this?

\[ \frac{\text{d} \mathbf{ f}_L}{\text{d} \mathbf{ w}} = \frac{\text{d} \mathbf{ f}_L}{\text{d} \mathbf{ f}_{L-1}} \frac{\text{d} \mathbf{ f}_{L-1}}{\text{d} \mathbf{ f}_{L-2}} \frac{\text{d} \mathbf{ f}_{L-2}}{\text{d} \mathbf{ f}_{L-3}} \cdots \frac{\text{d} \mathbf{ f}_3}{\text{d} \mathbf{ f}_{2}} \frac{\text{d} \mathbf{ f}_2}{\text{d} \mathbf{ f}_{1}} \frac{\text{d} \mathbf{ f}_1}{\text{d} \mathbf{ w}} \]

\[ \small \frac{\text{d} \mathbf{ f}_L}{\text{d} \mathbf{ w}} = \left( \left( \cdots \left( \left( \frac{\text{d} \mathbf{ f}_L}{\text{d} \mathbf{ f}_{L-1}} \frac{\text{d} \mathbf{ f}_{L-1}}{\text{d} \mathbf{ f}_{L-2}} \right) \frac{\text{d} \mathbf{ f}_{L-2}}{\text{d} \mathbf{ f}_{L-3}} \right) \cdots \frac{\text{d} \mathbf{ f}_3}{\text{d} \mathbf{ f}_{2}} \right) \frac{\text{d} \mathbf{ f}_2}{\text{d} \mathbf{ f}_{1}} \right) \frac{\text{d} \mathbf{ f}_1}{\text{d} \mathbf{ w}} \]

Or in a funky way?

\[ \frac{\text{d} \mathbf{ f}_L}{\text{d} \mathbf{ w}} = \frac{\text{d} \mathbf{ f}_L}{\text{d} \mathbf{ f}_{L-1}} \frac{\text{d} \mathbf{ f}_{L-1}}{\text{d} \mathbf{ f}_{L-2}} \frac{\text{d} \mathbf{ f}_{L-2}}{\text{d} \mathbf{ f}_{L-3}} \cdots \frac{\text{d} \mathbf{ f}_3}{\text{d} \mathbf{ f}_{2}} \frac{\text{d} \mathbf{ f}_2}{\text{d} \mathbf{ f}_{1}} \frac{\text{d} \mathbf{ f}_1}{\text{d} \mathbf{ w}} \]

\[ \small \frac{\text{d} \mathbf{ f}_L}{\text{d} \mathbf{ w}} = \frac{\text{d} \mathbf{ f}_L}{\text{d} \mathbf{ f}_{L-1}} \left( \left( \left( \frac{\text{d} \mathbf{ f}_{L-1}}{\text{d} \mathbf{ f}_{L-2}} \right) \frac{\text{d} \mathbf{ f}_{L-2}}{\text{d} \mathbf{ f}_{L-3}} \right) \left( \left( \cdots \frac{\text{d} \mathbf{ f}_3}{\text{d} \mathbf{ f}_{2}} \right) \frac{\text{d} \mathbf{ f}_2}{\text{d} \mathbf{ f}_{1}} \right) \right)\frac{\text{d} \mathbf{ f}_1}{\text{d} \mathbf{ w}} \]

Automatic differentiation

Forward-mode

\[ \small \frac{\text{d} \mathbf{ f}_L}{\text{d} \mathbf{ w}} = \frac{\text{d} \mathbf{ f}_L}{\text{d} \mathbf{ f}_{L-1}} \left( \frac{\text{d} \mathbf{ f}_{L-1}}{\text{d} \mathbf{ f}_{L-2}} \left( \frac{\text{d} \mathbf{ f}_{L-2}}{\text{d} \mathbf{ f}_{L-3}} \cdots \left( \frac{\text{d} \mathbf{ f}_3}{\text{d} \mathbf{ f}_{2}} \left( \frac{\text{d} \mathbf{ f}_2}{\text{d} \mathbf{ f}_{1}} \frac{\text{d} \mathbf{ f}_1}{\text{d} \mathbf{ w}} \right) \right) \cdots \right) \right) \]

Cost: \[ \small d_0 d_1 d_2 + d_0 d_2 d_3 + \ldots + d_0 d_{L-1} d_L= d_0 \sum_{\ell=2}^{L} d_\ell d_{\ell-1} \]

Automatic Differentiation

Reverse-mode

\[ \small \frac{\text{d} \mathbf{ f}_L}{\text{d} \mathbf{ w}} = \left( \left( \cdots \left( \left( \frac{\text{d} \mathbf{ f}_L}{\text{d} \mathbf{ f}_{L-1}} \frac{\text{d} \mathbf{ f}_{L-1}}{\text{d} \mathbf{ f}_{L-2}} \right) \frac{\text{d} \mathbf{ f}_{L-2}}{\text{d} \mathbf{ f}_{L-3}} \right) \cdots \frac{\text{d} \mathbf{ f}_3}{\text{d} \mathbf{ f}_{2}} \right) \frac{\text{d} \mathbf{ f}_2}{\text{d} \mathbf{ f}_{1}} \right) \frac{\text{d} \mathbf{ f}_1}{\text{d} \mathbf{ w}} \]

Cost: \[ \small d_Ld_{L-1}d_{L-2} + d_{L}d_{L-2} d_{L-3} + \ldots + d_Ld_{1} d_0 = d_L\sum_{\ell=0}^{L-2}d_\ell d_{\ell+1} \]

Memory cost of autodiff

Forward-mode

Store only:

• current activation \(\mathbf{ f}_l\) (\(d_l\))
• running JVP of size \(d_0 \times d_l\)
• current Jacobian \(d_l \times d_{l+1}\)

Reverse-mode

Cache activations \(\{\mathbf{ f}_l\}\) so local Jacobians can be applied during backward; higher memory than forward-mode.

Automatic differentiation

• in deep learning we’re most interested in scalar objectives
• \(d_L=1\), consequently, backward mode is always optimal
• in the context of neural networks this is backpropagation.
• backprop has higher memory cost than forwardprop

Backprop in deep networks

Autodiff: Practical Details

• Terminology: forward-mode = JVP; reverse-mode = VJP
• Non-scalar outputs: seed vector required (e.g. backward(grad_outputs))
• Stopping grads: .detach(), no_grad() in PyTorch

Autodiff: Practical Details

• Grad accumulation: .grad accumulates by default; call zero_grad()
• Memory: backprop caches intermediates; use checkpointing/rematerialisation
• Mixed-mode: combine forward+reverse for Hessian-vector products

Computational Graphs and PyTorch Autodiff

• Nodes: tensors and ops; Edges: data dependencies
• Forward pass caches intermediates needed for backward
• Backward pass applies local Jacobian-vector products

Overparameterised Systems

• Neural networks are highly overparameterised.
• If we could examine their Hessian at “optimum”
  • Very low (or negative) eigenvalues.
  • Error function is not sensitive to changes in parameters.
  • Implies parmeters are badly determined

Whence Generalisation?

• Not enough regularisation in our objective functions to explain.
• Neural network models are not using traditional generalisation approaches.
• The ability of these models to generalise must be coming somehow from the algorithm*
• How to explain it and control it is perhaps the most interesting theoretical question for neural networks.

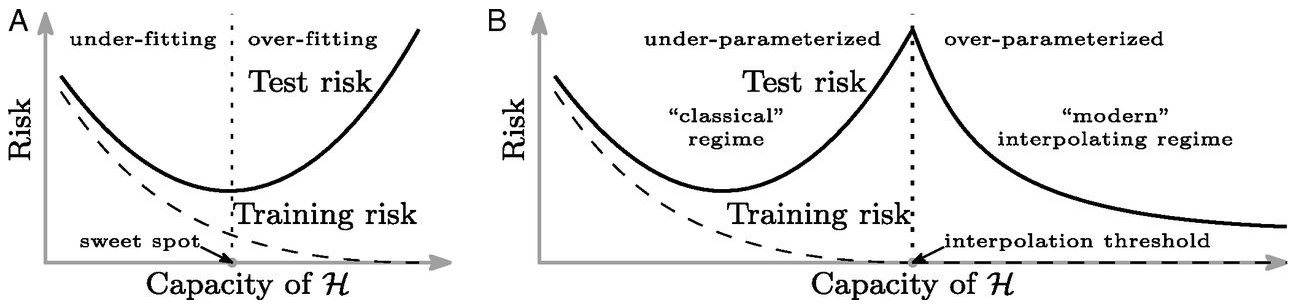
Double Descent

Neural Tangent Kernel

• Consider very wide neural networks.
• Consider particular initialisation.
• Deep neural network is regularising with a particular kernel.
• This is known as the neural tangent kernel (Jacot et al., 2018).

Regularization in Optimization

• Gradient flow methods allow us to study nature of optima.
• In particular systems, with given initialisations, we can show L1 and L2 norms are minimised.
• In other cases the rank of \(\mathbf{W}\) is minimised.
• Questions remain over the nature of this regularisation in neural networks.

Deep Linear Models

\[ f(\mathbf{ x}; \mathbf{W}) = \mathbf{W}_4 \mathbf{W}_3 \mathbf{W}_2 \mathbf{W}_1 \mathbf{ x}. \]

\[ \mathbf{W}= \mathbf{W}_4 \mathbf{W}_3 \mathbf{W}_2 \mathbf{W}_1 \]

Practical Optimisation Notes

• Initialisation: variance-preserving (He, Xavier); scale affects signal propagation
• Optimisers: SGD(+momentum), Adam/AdamW; decoupled weight decay often preferable
• Learning rate schedules: cosine, step, warmup; LR is the most sensitive hyperparameter
• Batch size: affects gradient noise and implicit regularisation; tune with LR
• Normalisation: BatchNorm/LayerNorm stabilise optimisation
• Regularisation: data augmentation, dropout, weight decay; early stopping

Further Reading

• Baydin et al. (2018) Automatic differentiation in ML (JMLR)
• Jacot, Gabriel, Hongler (2018) Neural Tangent Kernel
• Arora et al. (2019) On exact dynamics of deep linear networks
• Keskar et al. (2017) Large-batch training and sharp minima
• Novak et al. (2018) Sensitivity and generalisation in neural networks
• JAX Autodiff Cookbook (JVPs/VJPs, jacfwd/jacrev)
• PyTorch Autograd Docs (computational graph, grad_fn, backward)

Example: calculating a Hessian

\[ H(\mathbb{w}) = \frac{\text{d}^2}{\text{d}\mathbf{ w}\text{d}\mathbf{ w}^\top} L(\mathbf{ w}) := \frac{\text{d}}{\text{d}\mathbf{ w}} \mathbf{g}(\mathbf{ w}) \]

Example: Hessian-vector product

\[ \mathbf{v}^\top H(\mathbf{ w}) = \frac{\text{d}}{\text{d}\mathbf{ w}} \left( \mathbf{v}^\top \mathbf{g}(\mathbf{ w}) \right) \]