Abstract

In this session we use our understanding of objective functions to build a simple recommender system based on matrix factorisation.

ML Foundations Course Notebook Setup

We install some bespoke codes for creating and saving plots as well as loading data sets.

%%capture
%pip install notutils
%pip install pods
%pip install git+https://github.com/lawrennd/mlai.git

import notutils
import pods
import mlai
import mlai.plot as plot

Across the first week we motivated the importance of probability, but also stressed that machine learning builds on ‘objective functions.’ In this practical you will take the ideas you’ve learnt and apply them to the domain of collaborative filtering. Specifically you will create a matrix factorisation algorithm.

In the last few practicals we saw how we could load in a data set to pandas and use it for some simple data processing. We computed variaous probabilities on the data and I encouraged you to think about what sort of probabilities you need for prediction. This week we are going to take a slightly different tack.

Broadly speaking there are two dominating approaches to machine learning problems. We started to consider both approaches last week: firstly we can construct models based on defining the relationship between variables using probabilities. In this practical we will consider the second approach: which involves defining an objective function and optimising it.

What do we mean by an objective function? An objective function could be an error function a cost function or a benefit function. In evolutionary computing they are called fitness functions. But the idea is always the same. We write down a mathematical equation which is then optimized to do the learning. The equation should be a function of the data and our model parameters. We have a choice when optimizing, either minimize or maximize. To avoid confusion, in the optimization field, we always choose to minimize the function. If we have function that we would like to maximize, we simply choose to minimize the negative of that function.

So for this lab session, we are going to ignore probabilities, but don’t worry, they will return!

This week we are going to try and build a simple movie recommender system using an objective function. To do this, the first thing I’d like you to do is to install some software we’ve written for sharing information across google documents.

Movie Violence Data

This is a data set created by Simon Garnier and Rany Olson for exploring the differences between R and Python for data science. The data contains information about different movies augmented by estimates about how many on-screen deaths are contained in the movie. The data is craped from http://www.moviebodycounts.com. The data contains the following featuers for each movie: Year, Body_Count, MPAA_Rating, Genre, Director, Actors, Length_Minutes, IMDB_Rating.

import pods

data = pods.datasets.movie_body_count()
movies = data['Y']

The data is provided to us in the form of a pandas data frame, we can see the features we’re provided with by inspecting the columns of the data frame.

print(', '.join(movies.columns))

Once it is loaded in the data can be summarized using the describe method in pandas.

Plotting the Data

print(movies['Year'])
#print(movies['Body_Count'])

This shows the number of deaths per film across the years. We can plot the data as follows.

# this ensures the plot appears in the web browser
%matplotlib inline 
import matplotlib.pyplot as plt # this imports the plotting library in python

plt.plot(movies['Year'], movies['Body_Count'], 'rx')

You may be curious what the arguments we give to plt.plot are for, now is the perfect time to look at the documentation

plt.plot?

We immediately note that some films have a lot of deaths, which prevent us seeing the detail of the main body of films. First lets identify the films with the most deaths.

movies[movies['Body_Count']>200]

Here we are using the command movies['Kill_Count']>200 to index the films in the pandas data frame which have over 200 deaths. To sort them in order we can also use the sort command. The result of this command on its own is a data series of True and False values. However, when it is passed to the data data frame it returns a new data frame which contains only those values for which the data series is True. We can also sort the result. To sort the result by the values in the Kill_Count column in descending order we use the following command.

movies[movies['Body_Count']>200].sort_values(by='Body_Count', ascending=False)

We now see that the ‘Lord of the Rings’ is a large outlier with a very large number of kills. We can try and determine how much of an outlier by histograming the data.

Plotting the Data

movies['Body_Count'].hist(bins=20) # histogram the data with 20 bins.
plt.title('Histogram of Film Kill Count')

Exercise 1

Read on the internet about the following python libraries: numpy, matplotlib, scipy and pandas. What functionality does each provide python. What is the pylab library and how does it relate to the other libraries?

We could try and remove these outliers, but another approach would be plot the logarithm of the counts against the year.

plt.plot(movies['Year'], movies['Body_Count'], 'rx')
ax = plt.gca() # obtain a handle to the current axis
ax.set_yscale('log') # use a logarithmic death scale
# give the plot some titles and labels
plt.title('Film Deaths against Year')
plt.ylabel('deaths')
plt.xlabel('year')

Note a few things. We are interacting with our data. In particular, we are replotting the data according to what we have learned so far. We are using the progamming language as a scripting language to give the computer one command or another, and then the next command we enter is dependent on the result of the previous. This is a very different paradigm to classical software engineering. In classical software engineering we normally write many lines of code (entire object classes or functions) before compiling the code and running it. Our approach is more similar to the approach we take whilst debugging. Historically, researchers interacted with data using a console. A command line window which allowed command entry. The notebook format we are using is slightly different. Each of the code entry boxes acts like a separate console window. We can move up and down the notebook and run each part in a different order. The state of the program is always as we left it after running the previous part.

Exercise 2

Data ethics. If you find data available on the internet, can you simply use it without consequence? If you are given data by a fellow researcher can you publish that data on line?

Recommender Systems

A recommender system aims to make suggestions for items (films, books, other commercial products) given what it knows about users’ tastes. The recommendation engine needs to represent the taste of all the users and the characteristics of each object.

A common way for organizing objects is to place related objects spatially close together. For example in a library we try and put books that are on related topics near to each other on the shelves. One system for doing this is known as Dewey Decimal Classification. In the Dewey Decimal Classification system (which dates from 1876) each subject is given a number (in fact it’s a decimal number). For example, the field of Natural Sciences and Mathematics is given numbers which start with 500. Subjects based on Computer Science are given numbers which start 004 and works on the ‘mathematical principles’ of Computer science are given the series 004.0151 (which we might store as 4.0151 on a Computer). Whilst it’s a classification system, the books in the library are typically laid out in the same order as the numbers, so we might expect that neighbouring numbers represent books that are related in subject. That seems to be exactly what we want when also representing films. Could we somehow represent each film’s subject according to a number? In a similar way we could then imagine representing users with a list of numbers that represent things that each user is interested in.

Actually a one dimensional representation of a subject can be very awkward. To see this, let’s have a look at the Dewey Decimal Classification numbers for the 900s, which is listed as ‘History and Geography.’ We will focus on subjects in the 940s which can be found in this list from Nova Southeastern University. Whilst the ordering for places is somewhat sensible, it is also rather arbitrary. In the 940s we have Europe listed from 940-949, Asia listed from 950-959 and Africa listed from 960-969. Whilst it’s true that Asia borders Europe, Africa is also very close, and the history of the Roman Empire spreads into Carthage and later on Egypt. This image from Wikipedia shows a map of the Cathaginian Empire which fell after fighting with Rome.

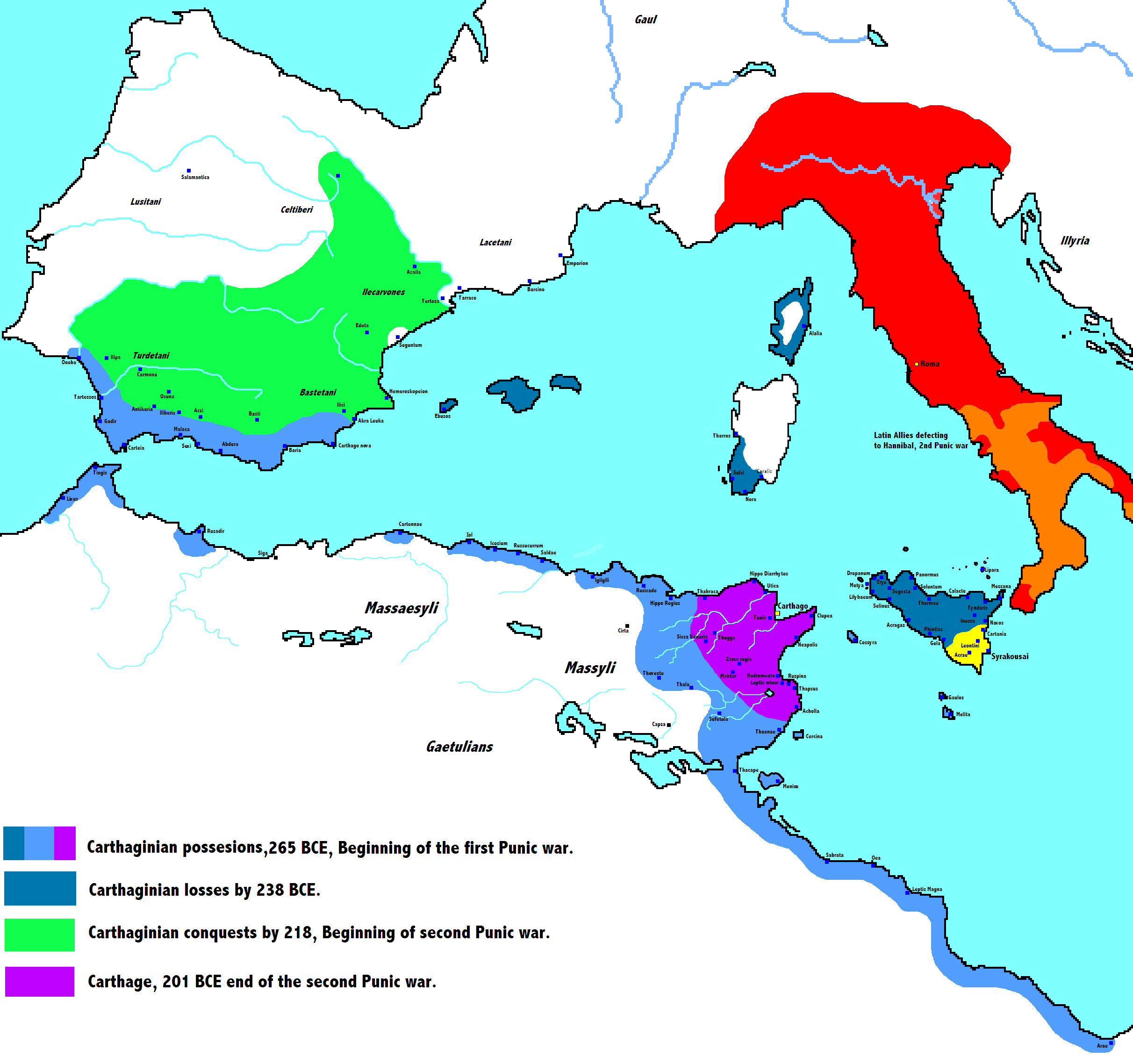
Figure: The Carthaginian Empire at its peak.

We now need to make a decision about whether Roman Histories are European or African, ideally we’d like them to be somewhere between the two, but we can’t place them there in the Dewey Decimal system because between Europe and Africa is Asia, which has less to do with the Roman Empire than either Europe or Africa. Of course the fact that we’ve used a map provides a clue as to what to do next. Libraries are actually laid out on floors, so what if we were to use the spatial lay out to organise the sujbects of the books in two dimensions. Books on Geography could be laid out according to where in the world they are referring to.

Such complexities are very hard to encapsulate in one number, but inspired by the map examples we can start considering how we might lay out films in two dimensions. Similarly, we can consider laying out a map of people’s interests. If the two maps correspond to one another, the map of people could reflect where they might want to live in ‘subject space.’ We can think of representing people’s tastes as where they might best like to sit in the library to access easily the books they are most interested in.

Inner Products for Representing Similarity

Ideas like the above are good for gaining intuitions about what we might want, but the one of the skills of data science is representing those ideas mathematically. Mathematical abstraction of a problem is one of the key ways in which we’ve been able to progress as a society. Understanding planetary motions, as well as those of the smallest molecule (to quote Laplace’s Philosophical Essay on Probabilities) needed to be done mathematically. The right mathematical model in machine learning can be slightly more elusive, because constructing it is a two stage process.

1. We have to determine the right intuition for the system we want to represent. Notions such as ‘subject’ and ‘interest’ are not mathematically well defined, and even when we create a new interpretation of what they might mean, each interpretation may have its own weaknesses.

2. Once we have our interpretation we can attempt to mathematically formalize it. In our library interpretation, that’s what we need to do next.

The Library on an Infinite Plane

Let’s imagine a library which stores all the items we are interested in, not just books, but films and shopping items too. Such a library is likely to be very large, so we’ll create it on an infinite two dimensional plane. This means we can use all the real numbers to represent the location of each item on the plane. For a two dimensional plane, we need to store the locations in a vector of numbers: we can decide that the \(j\)th item’s location in the library is given by \[ \mathbf{v}_j = \begin{bmatrix} v_{j,1} \\ v_{j,2}\end{bmatrix}, \] where \(v_{j,1}\) represents the \(j\)th item’s location in the East-West direction (or the \(x\)-axis) and \(v_{j,2}\) represents the \(j\)th item’s location in the North-South direction (or the \(y\)-axis). Now we need to specify the location where each user sits so that all the items that interest them are nearby: we can also represent the \(i\)th user’s location with a vector \[ \mathbf{u}_i = \begin{bmatrix} u_{i,1} \\ u_{i,2}\end{bmatrix}. \] Finally, we need some way of recording a given user’s affinity for a given item. This affinity might be the rating that the user gives the film. We can use \(y_{i,j}\) to represent user \(i\)’s affinity for item \(j\).

For our film example we might imagine wanting to order films in a few ways. We could imagine organising films in the North-South direction as to how romantic they are. We could place the more romantic films further North and the less romantic films further South. For the East-West direction we could imagine ordering them according to how historic they are: we can imagine placing science fiction films to the East and historical drama to the West. In this case, fans of historical romances would be based in the North-West location, whilst fans of Science Fiction Action films might be located in the South-East (if we assume that ‘Action’ is the opposite of ‘Romance,’ which is not necessarily the case). How do we lay out all these films? Have we got the right axes? In machine learning the answer is to ‘let the data speak.’ Use the data to try and obtain such a lay out. To do this we first need to obtain the data.

Collecting the Data

This functionality involves some prewritten code which connects to a central write server, where you can rate movies that you’ve seen.

Once you have placed your ratings, we can download the data to a file. We will build an algorithm on these ratings and use them to make predictions for the rest of the class. Firstly, here’s the code for which movies we will be rating. Remember to change your name.

import pandas as pd
import os
movies_list = [
    # Kenyan films
    "Nairobi Half Life",
    "Rafiki",
    "Sincerely Daisy",
    "Supa Modo",
    "Kati Kati",
    "Mvera",
    "NAWI: Dear Future Me",
    "BOBO",
    "The First Grader",
    "Mother Mother",
    "The Wall Street Boy",
    "40 Sticks",
    "TeraStorm",

    # Global all-time blockbuster hits
    "Avatar",
    "Avengers: Endgame",
    "Titanic",
    "The Lion King",
    "Frozen",
    "Spider-Man: No Way Home",
    "Black Panther",
    "Top Gun: Maverick",
    "The Dark Knight",
    "Inception",
    "Jurassic World",
    "Minions: The Rise of Gru",
    "The Fate of the Furious",
    "Doctor Strange in the Multiverse of Madness",
    "Furious 7",
    "Star Wars: The Force Awakens",
    "The Avengers",
    "Beauty and the Beast",
    "Harry Potter and the Deathly Hallows – Part 2",
    "Joker",
    "Aladdin",
    "Aquaman"
]

name = 'todo' # TODO: your name here - this will be somewhat public so you might not want to use full real names, nickname is fine
assert name!='todo'

The below code starts an interactive Python Widget, which will submit your responses. There’s also code for reading the ratings after they’ve been submitted.

import random, requests, ipywidgets as W
from ipywidgets import Widget
from IPython.display import display, clear_output
import json

# Config
topic, target = "mlfc_movie_ratings", 25
url = f"https://ntfy.sh/{topic}"
cache = "rated_movies_cache.txt"

def responses(topic=topic, sep="|||", since="all", n=None):
    url = f"https://ntfy.sh/{topic}/json?poll=1&since={since}"
    rows = []
    with requests.get(url, stream=True) as r:
        for line in r.iter_lines():
            if not line: continue
            e = json.loads(line)
            if e.get("event") != "message": continue
            p = (e.get("message") or "").split(sep)
            rows.append({"user": p[0], "film": p[1], "rating": pd.to_numeric(p[2], errors="coerce")} if len(p)==3 else {"raw": e.get("message")})
            if n and len(rows) >= n: break
    return pd.DataFrame(rows)

def start_movie_rater(movies_list=movies_list, topic=topic, name=name, target=25):
    import random, requests
    import ipywidgets as W
    from IPython.display import display

    url = f"https://ntfy.sh/{topic}"
    movies = list(dict.fromkeys(map(str, movies_list)))
    seen = set()  # in-memory only
    rated, cur, running = 0, None, True

    def rem(): return [m for m in movies if m not in seen]
    def mark_seen(m):
        if m not in seen:
            seen.add(m)
    def send(m, r):
        try:
            requests.post(url, data=f"{name}|||{m}|||{r}".encode("utf-8"), timeout=3)
        except Exception:
            pass

    status = W.HTML()
    btns = [W.Button(description=str(i)) for i in range(1, 11)]
    skip = W.Button(description="Skip", button_style="warning")
    finish = W.Button(description="Finish", button_style="success")
    box = W.VBox([status, W.HBox(btns + [skip, finish])])

    def end(msg):
        nonlocal running
        running = False
        for w in btns + [skip, finish]:
            w.disabled = True
        status.value = msg

    def pick_next():
        nonlocal cur
        r = rem()
        cur = random.choice(r) if r else None
        status.value = f"<b>Rate ({rated}/{target}):</b> {cur}" if cur else ""

    def on_rate(b):
        nonlocal rated
        if not running or cur is None:
            return
        send(cur, int(b.description))
        mark_seen(cur)
        rated += 1
        if rated >= target:
            end(f"Done. Rated {rated}.")
            return
        pick_next()
        if cur is None:
            end(f"No unseen movies left. Rated {rated}.")

    def on_skip(_):
        if not running or cur is None:
            return
        mark_seen(cur)
        pick_next()
        if cur is None:
            end(f"No unseen movies left. Rated {rated}.")

    def on_finish(_):
        end(f"Finished. Rated {rated}.")

    for b in btns:
        b.on_click(on_rate)
    skip.on_click(on_skip)
    finish.on_click(on_finish)

    display(box)
    pick_next()
    if cur is None:
        end("No unseen movies to rate.")

# run this cell to provide your ratings
Widget.close_all()
start_movie_rater(target=5)

# run this cell to collect everyone's responses
Y = responses()
Y

Processing the Data

Exercise 3

What is a pivot table? What does the pandas command pd.pivot_table do? Subsequently, what does pd.melt do?

Exercise 4

Convert the above DataFrame Y to a pivot table, and then back again to its current form.

Measuring Similarity

We now need a measure for determining the similarity between the item and the user: how close the user is sitting to the item in the rooom if you like. We are going to use the inner product between the vector representing the item and the vector representing the user.

An inner product (or dot product) between two vectors \(\mathbf{a}\) and \(\mathbf{b}\) is written as \(\mathbf{a}\cdot\mathbf{b}\). Or in vector notation we sometimes write it as \(\mathbf{a}^\top\mathbf{b}\). An inner product is simply the sume of the products of each element of the vector, \[ \mathbf{a}^\top\mathbf{b} = \sum_{i} a_i b_i \] The inner product can be seen as a measure of similarity. The inner product gives us the cosine of the angle between the two vectors multiplied by their length. The smaller the angle between two vectors the larger the inner product. \[ \mathbf{a}^\top\mathbf{b} = |\mathbf{a}||\mathbf{b}| \cos(\theta) \] where \(\theta\) is the angle between two vectors and \(|\mathbf{a}|\) and \(|\mathbf{b}|\) are the respective lengths of the two vectors.

Since we want each user to be sitting near each item, then we want the inner product to be large for any two items which are rated highly by that user. We can do this by trying to force the inner product \(\mathbf{u}_i^\top\mathbf{v}_j\) to be similar to the rating given by the user, \(y_{i,j}\). To ensure this we will use a least squares objective function for all user ratings.

Objective Function

The error function (or objective function, or cost function) we will choose is known as ‘sum of squares,’ we will aim to minimize the sum of squared squared error between the inner product of \(\mathbf{u}_i\) and \(\mathbf{v}_i\) and the observed score for the user/item pairing, given by \(y_{i, j}\).

The total objective function can be written as \[ E(\mathbf{U}, \mathbf{V}) = \sum_{i,j} s_{i,j} (y_{i,j} - \mathbf{u}_i^\top \mathbf{v}_j)^2 \] where \(s_{i,j}\) is an indicator variable that is 1 if user \(i\) has rated item \(j\) and is zero otherwise. Here \(\mathbf{U}\) is the matrix made up of all the vectors \(\mathbf{u}\), \[ \mathbf{U} = \begin{bmatrix} \mathbf{u}_1 \dots \mathbf{u}_n\end{bmatrix}^\top \] where we note that \(i\)th row of \(\mathbf{U}\) contains the vector associated with the \(i\)th user and \(n\) is the total number of users. This form of matrix is known as a design matrix. Similarly, we define the matrix \[ \mathbf{V} = \begin{bmatrix} \mathbf{v}_1 \dots \mathbf{v}_m\end{bmatrix}^\top \] where again the \(j\)th row of \(\mathbf{V}\) contains the vector associated with the \(j\)th item and \(m\) is the total number of items in the data set.

Objective Optimization

The idea is to mimimize this objective. A standard, simple, technique for minimizing an objective is gradient descent or steepest descent. In gradient descent we simply choose to update each parameter in the model by subtracting a multiple of the objective function’s gradient with respect to the parameters. So for a parameter \(u_{i,j}\) from the matrix \(\mathbf{U}\) we would have an update as follows: \[ u_{k,\ell} \leftarrow u_{k,\ell} - \eta \frac{\text{d} E(\mathbf{U}, \mathbf{V})}{\text{d}u_{k,\ell}} \] where \(\eta\) (which is pronounced eta in English) is a Greek letter representing the learning rate.

We can compute the gradient of the objective function with respect to \(u_{k,\ell}\) as \[ \frac{\text{d}E(\mathbf{U}, \mathbf{V})}{\text{d}u_{k,\ell}} = -2 \sum_j s_{k,j}v_{j,\ell}(y_{k, j} - \mathbf{u}_k^\top\mathbf{v}_{j}). \] Similarly each parameter \(v_{i,j}\) needs to be updated according to its gradient.

Exercise 5

What is the gradient of the objective function with respect to \(v_{k, \ell}\)? Write your answer in the box below, and explain which differentiation techniques you used to get there. You will be expected to justify your answer in class by oral questioning. Create a function for computing this gradient that is used in the algorithm below.

Steepest Descent Algorithm

In the steepest descent algorithm we aim to minimize the objective function by subtacting the gradient of the objective function from the parameters.

Initialisation

To start with though, we need initial values for the matrix \(\mathbf{U}\) and the matrix \(\mathbf{V}\). Let’s create them as pandas data frames and initialise them randomly with small values.

import numpy as np

q = 2 # the dimension of our map of the 'library'
learn_rate = 0.01
U = pd.DataFrame(np.random.normal(size=(len(Y['user'].unique()), q))*0.001, index=Y['user'].unique())
V = pd.DataFrame(np.random.normal(size=(len(Y['film'].unique()), q))*0.001, index=Y['film'].unique())

We also will subtract the mean from the rating before we try and predict them predictions. Have a think about why this might be a good idea (Hint: what will the gradients be if we don’t subtract the mean?).

Y['rating'] -= Y['rating'].mean()

Now that we have the initial values set, we can start the optimization. First we define a function for the gradient of the objective and the objective function itself.

def objective_gradient(Y, U, V):
    gU = pd.DataFrame(np.zeros((U.shape)), index=U.index)
    gV = pd.DataFrame(np.zeros((V.shape)), index=V.index)
    obj = 0.
    for ind, series in Y.iterrows():
        film = series['film']
        user = series['user']
        rating = series['rating']
        prediction = np.dot(U.loc[user], V.loc[film]) # vTu
        diff = prediction - rating # vTu - y
        obj += diff*diff
        gU.loc[user] += 2*diff*V.loc[film]
        gV.loc[film] += 2*diff*U.loc[user]
    return obj, gU, gV

Now we can write our simple optimisation route. This allows us to observe the objective function as the optimization proceeds.

import sys
iterations = 100
for i in range(iterations):
    obj, gU, gV = objective_gradient(Y, U, V)
    print("Iteration", i, "Objective function: ", obj)
    U -= learn_rate*gU
    V -= learn_rate*gV

Next we’ll use plotly to create a simple interactive visualisation of the users and the films. In our map, we expect similar films to be close to each other and similar users to be close to each other. Let’s look at the user map first, which is stored in the dataframe U.

Now let’s look at our map of the films which is stored in a dataframe V.

That gives us a first attempt at visualising this rating data.

Exercise 6

What happens as you increase the number of iterations? What happens if you increase the learning rate?

Stochastic Gradient Descent or Robbins Monroe Algorithm

{In we saw how stochastic gradient descent (Robbins and Monro, 1951) involves updating separating each gradient update according to each separate observation, rather than summing over them all. It is an approximate optimization method, but it has proven convergence under certain conditions and can be much faster in practice. It is used widely by internet companies for doing machine learning in practice. For example, Facebook’s ad ranking algorithm uses stochastic gradient descent.

Exercise 7

Create a stochastic gradient descent version of the algorithm. Monitor the objective function after every 1000 updates to ensure that it is decreasing. When you have finished, plot the movie map and the user map in two dimensions. Label the plots with the name of the movie or user.

Making Predictions

Predictions can be made from the model of the appropriate rating for a given user, \(i\), for a given film, \(j\), by simply taking the inner product between their vectors \(\mathbf{u}_i\) and \(\mathbf{v}_j\).

Is Our Map Enough? Are Our Data Enough?

Is two dimensions really enough to capture the complexity of humans and their artforms? Perhaps we need even more dimensions to capture that complexity. Extending our books analogy further, consider how we should place books that have a historical timeframe as well as some geographical location. Do we really want books from the 2nd World War to sit alongside books from the Roman Empire? Books on the American invasion of Sicily in 1943 are perhaps less related to books about Carthage than those that study the Jewish Revolt from 66-70 (in the Roman Province of Judaea). So books that relate to subjects which are closer in time should be stored together. However, a student of rebellion against empire may also be interested in the relationship between the Jewish Revolt of 66-70 and the Indian Rebellion of 1857, nearly 1800 years later. Whilst the technologies are different, the psychology of the people is shared: a rebellious nation angainst their imperial masters, triggered by misrule with a religious and cultural background. To capture such complexities we would need further dimensions in our latent representation. But are further dimensions justified by the amount of data we have? Can we really understand the facets of a film that only has at most three or four ratings?

Going Further

If you want to take this model further then you’ll need more data. One possible source of data is the movielens data set. They have data sets containing up to ten million movie ratings. The few ratings we were able to collect in the class are not enough to capture the rich structure underlying these films. Imagine if we assume that the ratings are uniformly distributed between 1 and 5. If you know something about information theory then you could use that to work out the maximum number of bits of information we could gain per rating.

Now we’ll download the movielens 100k data and see if we can extract information about these movies.

import pods

d = pods.datasets.movielens100k()
Y=d['Y']

Exercise 8

Use stochastic gradient descent to make a movie map for the movielens data. Plot the map of the movies when you are finished.

End of Practical 4

 _______  __   __  _______  __    _  ___   _  _______  __
|       ||  | |  ||   _   ||  |  | ||   | | ||       ||  |
|_     _||  |_|  ||  |_|  ||   |_| ||   |_| ||  _____||  |
  |   |  |       ||       ||       ||      _|| |_____ |  |
  |   |  |       ||       ||  _    ||     |_ |_____  ||__|
  |   |  |   _   ||   _   || | |   ||    _  | _____| | __
  |___|  |__| |__||__| |__||_|  |__||___| |_||_______||__|

Thanks!

For more information on these subjects and more you might want to check the following resources.

• company: Trent AI
• book: The Atomic Human
• twitter: @lawrennd
• podcast: The Talking Machines
• newspaper: Guardian Profile Page
• blog: http://inverseprobability.com

References