Generalization: Model Validation

Review

• Last time: introduced basis functions.
• Showed how to maximize the likelihood of a non-linear model that’s linear in parameters.
• Explored the different characteristics of different basis function models

Alan Turing

Probability Winning Olympics?

• He was a formidable Marathon runner.
• In 1946 he ran a time 2 hours 46 minutes.
  • That’s a pace of 3.95 min/km.
• What is the probability he would have won an Olympics if one had been held in 1946?

Expected Loss

\[ R(\mathbf{ w}) = \int L(y, x, \mathbf{ w}) \mathbb{P}(y, x) \text{d}y \text{d}x. \]

Sample-Based Approximations

• Sample based approximation: replace true expectation with sum over samples. \[ \int f(z) p(z) \text{d}z\approx \frac{1}{s}\sum_{i=1}^s f(z_i). \]

• Allows us to approximate true integral with a sum \[ R(\mathbf{ w}) \approx \frac{1}{n}\sum_{i=1}^{n} L(y_i, x_i, \mathbf{ w}). \]

Empirical Risk Minimization

• If the loss is the squared loss \[ L(y, x, \mathbf{ w}) = (y-\mathbf{ w}^\top\boldsymbol{\phi}(x))^2, \]
• This recovers the empirical risk \[ R(\mathbf{ w}) \approx \frac{1}{n} \sum_{i=1}^{n} (y_i - \mathbf{ w}^\top \boldsymbol{\phi}(x_i))^2 \]

Estimating Risk through Validation

Validation

Olympic Marathon Data

Gold medal times for Olympic Marathon since 1896. Marathons before 1924 didn’t have a standardized distance. Present results using pace per km. In 1904 Marathon was badly organized leading to very slow times.

Image from Wikimedia Commons http://bit.ly/16kMKHQ

Olympic Marathon Data

Validation on the Olympic Marathon Data

Polynomial Fit: Training Error

The next thing we’ll do is consider a quadratic fit. We will compute the training error for the two fits.

Polynomial Fits to Olympics Data

❮ ❯

Hold Out Validation on Olympic Marathon Data

Overfitting

• Increase number of basis functions we obtain a better ‘fit’ to the data.
• How will the model perform on previously unseen data?
• Let’s consider predicting the future.

Future Prediction: Extrapolation

❮ ❯

Extrapolation

• Here we are training beyond where the model has learnt.
• This is known as extrapolation.
• Extrapolation is predicting into the future here, but could be:
  • Predicting back to the unseen past (pre 1892)
  • Spatial prediction (e.g. Cholera rates outside Manchester given rates inside Manchester).

Interpolation

• Predicting the wining time for 1946 Olympics is interpolation.
• This is because we have times from 1936 and 1948.
• If we want a model for interpolation how can we test it?
• One trick is to sample the validation set from throughout the data set.

Future Prediction: Interpolation

❮ ❯

Choice of Validation Set

• The choice of validation set should reflect how you will use the model in practice.
• For extrapolation into the future we tried validating with data from the future.
• For interpolation we chose validation set from data.
• For different validation sets we could get different results.

Leave One Out Validation

Leave One Out Error

• Take training set and remove one point.
• Train on the remaining data.
• Compute the error on the point you removed (which wasn’t in the training data).
• Do this for each point in the training set in turn.
• Average the resulting error.
• This is the leave one out error.

Leave One Out Validation

fold ❮ ❯

\(k\)-fold Cross Validation

• Leave one out error can be very time consuming.
• Need to train your algorithm \(n\) times.
• An alternative: \(k\) fold cross validation.

\(k\)-fold Cross Validation

fold ❮ ❯

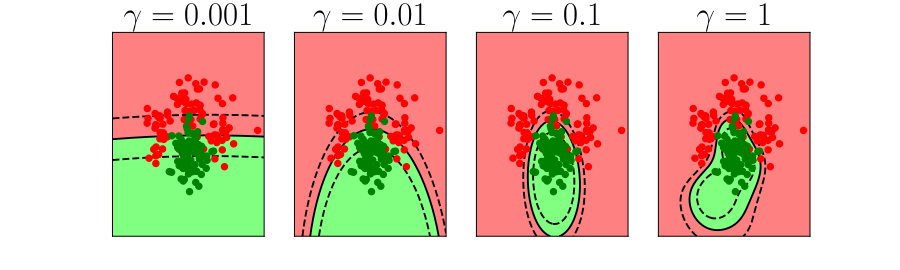
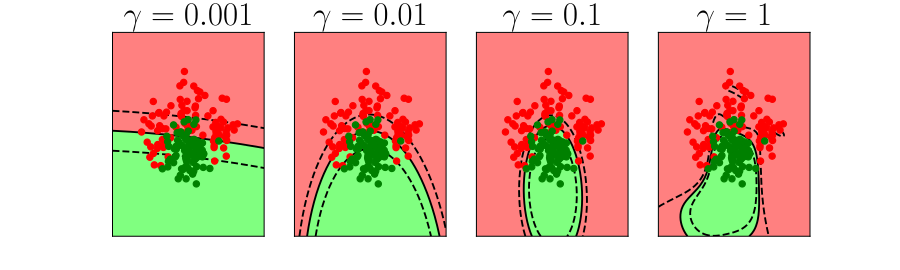
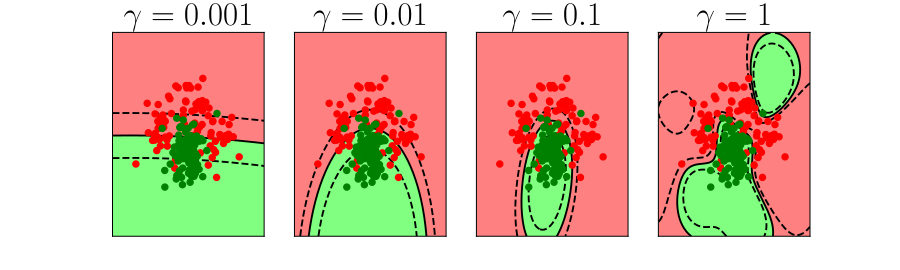
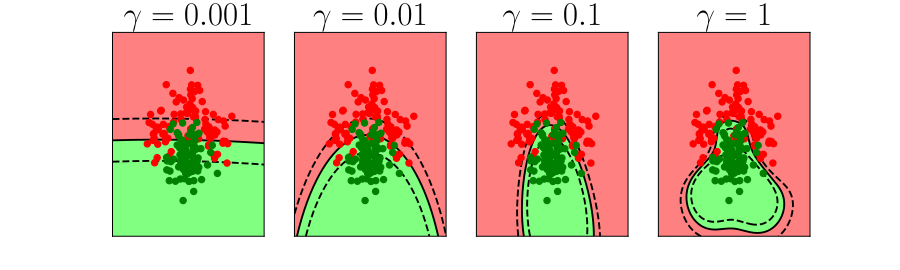
Bias Variance Decomposition

Generalisation error \[\begin{align*} R(\mathbf{ w}) = & \int \left(y- f^*(\mathbf{ x})\right)^2 \mathbb{P}(y, \mathbf{ x}) \text{d}y\text{d}\mathbf{ x}\\ & \triangleq \mathbb{E}\left[ \left(y- f^*(\mathbf{ x})\right)^2 \right]. \end{align*}\]

Decompose

Decompose as \[ \begin{align*} \mathbb{E}\left[ \left(y- f(\mathbf{ x})\right)^2 \right] = & \text{bias}\left[f^*(\mathbf{ x})\right]^2 \\ & + \text{variance}\left[f^*(\mathbf{ x})\right] \\ \\ &+\sigma^2, \end{align*} \]

Bias

• Given by \[ \text{bias}\left[f^*(\mathbf{ x})\right] = \mathbb{E}\left[f^*(\mathbf{ x})\right] - f(\mathbf{ x}) \]

• Error due to bias comes from a model that’s too simple.

Variance

• Given by \[ \text{variance}\left[f^*(\mathbf{ x})\right] = \mathbb{E}\left[\left(f^*(\mathbf{ x}) - \mathbb{E}\left[f^*(\mathbf{ x})\right]\right)^2\right]. \]

• Slight variations in the training set cause changes in the prediction. Error due to variance is error in the model due to an overly complex model.