Generalization: Model Validation
Review
- Last time: introduced basis functions.
- Showed how to maximize the likelihood of a non-linear model that’s linear in parameters.
- Explored the different characteristics of different basis function models
Alan Turing

|

|
Probability Winning Olympics?
- He was a formidable Marathon runner.
- In 1946 he ran a time 2 hours 46 minutes.
- That’s a pace of 3.95 min/km.
- What is the probability he would have won an Olympics if one had been held in 1946?
Expected Loss
\[ R(\mathbf{ w}) = \int L(y, x, \mathbf{ w}) \mathbb{P}(y, x) \text{d}y \text{d}x. \]
Sample-Based Approximations
Sample based approximation: replace true expectation with sum over samples. \[ \int f(z) p(z) \text{d}z\approx \frac{1}{s}\sum_{i=1}^s f(z_i). \]
Allows us to approximate true integral with a sum \[ R(\mathbf{ w}) \approx \frac{1}{n}\sum_{i=1}^{n} L(y_i, x_i, \mathbf{ w}). \]
Empirical Risk Minimization
- If the loss is the squared loss \[ L(y, x, \mathbf{ w}) = (y-\mathbf{ w}^\top\boldsymbol{\phi}(x))^2, \]
- This recovers the empirical risk \[ R(\mathbf{ w}) \approx \frac{1}{n} \sum_{i=1}^{n} (y_i - \mathbf{ w}^\top \boldsymbol{\phi}(x_i))^2 \]
Estimating Risk through Validation
Validation
Olympic Marathon Data
|

|
Olympic Marathon Data
Validation on the Olympic Marathon Data
Polynomial Fit: Training Error
The next thing we’ll do is consider a quadratic fit. We will compute the training error for the two fits.
Polynomial Fits to Olympics Data
Hold Out Validation on Olympic Marathon Data
Overfitting
- Increase number of basis functions we obtain a better ‘fit’ to the data.
- How will the model perform on previously unseen data?
- Let’s consider predicting the future.
Future Prediction: Extrapolation
Extrapolation
- Here we are training beyond where the model has learnt.
- This is known as extrapolation.
- Extrapolation is predicting into the future here, but could be:
- Predicting back to the unseen past (pre 1892)
- Spatial prediction (e.g. Cholera rates outside Manchester given rates inside Manchester).
Interpolation
- Predicting the wining time for 1946 Olympics is interpolation.
- This is because we have times from 1936 and 1948.
- If we want a model for interpolation how can we test it?
- One trick is to sample the validation set from throughout the data set.
Future Prediction: Interpolation
Choice of Validation Set
- The choice of validation set should reflect how you will use the model in practice.
- For extrapolation into the future we tried validating with data from the future.
- For interpolation we chose validation set from data.
- For different validation sets we could get different results.
Leave One Out Validation
Leave One Out Error
- Take training set and remove one point.
- Train on the remaining data.
- Compute the error on the point you removed (which wasn’t in the training data).
- Do this for each point in the training set in turn.
- Average the resulting error.
- This is the leave one out error.
Leave One Out Validation
fold
num basis
num basis
num basis
num basis
num basis
num basis
\(k\)-fold Cross Validation
- Leave one out error can be very time consuming.
- Need to train your algorithm \(n\) times.
- An alternative: \(k\) fold cross validation.
\(k\)-fold Cross Validation
fold
num basis
num basis
num basis
num basis
num basis
num basis
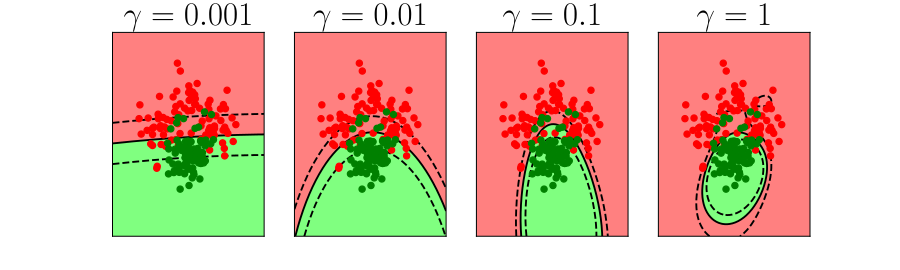
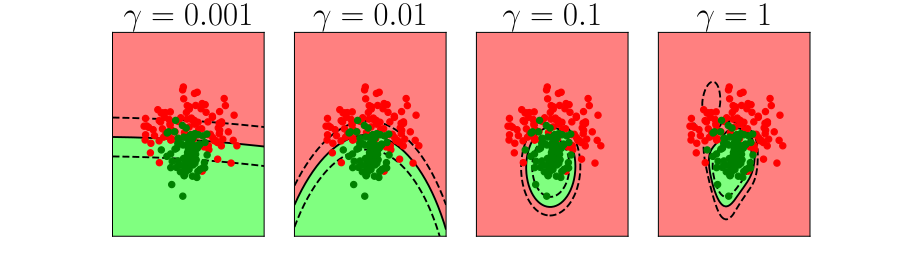
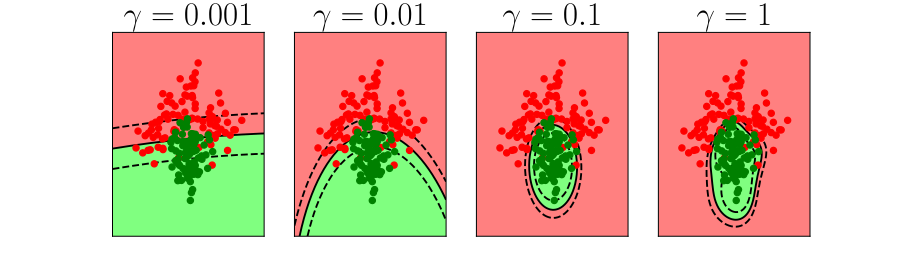
Bias Variance Decomposition
Generalisation error \[\begin{align*} R(\mathbf{ w}) = & \int \left(y- f^*(\mathbf{ x})\right)^2 \mathbb{P}(y, \mathbf{ x}) \text{d}y\text{d}\mathbf{ x}\\ & \triangleq \mathbb{E}\left[ \left(y- f^*(\mathbf{ x})\right)^2 \right]. \end{align*}\]
Decompose
Decompose as \[ \begin{align*} \mathbb{E}\left[ \left(y- f(\mathbf{ x})\right)^2 \right] = & \text{bias}\left[f^*(\mathbf{ x})\right]^2 \\ & + \text{variance}\left[f^*(\mathbf{ x})\right] \\ \\ &+\sigma^2, \end{align*} \]
Bias
Given by \[ \text{bias}\left[f^*(\mathbf{ x})\right] = \mathbb{E}\left[f^*(\mathbf{ x})\right] - f(\mathbf{ x}) \]
Error due to bias comes from a model that’s too simple.
Variance
Given by \[ \text{variance}\left[f^*(\mathbf{ x})\right] = \mathbb{E}\left[\left(f^*(\mathbf{ x}) - \mathbb{E}\left[f^*(\mathbf{ x})\right]\right)^2\right]. \]
Slight variations in the training set cause changes in the prediction. Error due to variance is error in the model due to an overly complex model.
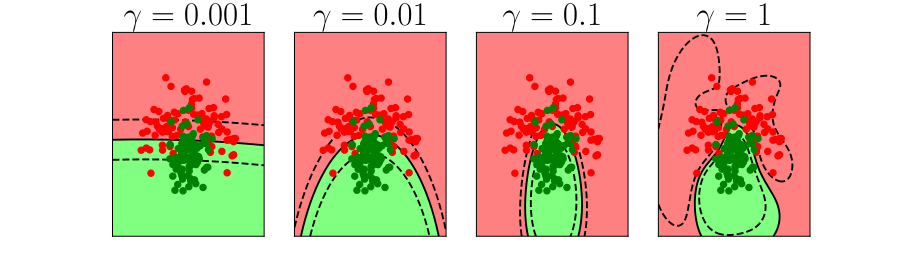
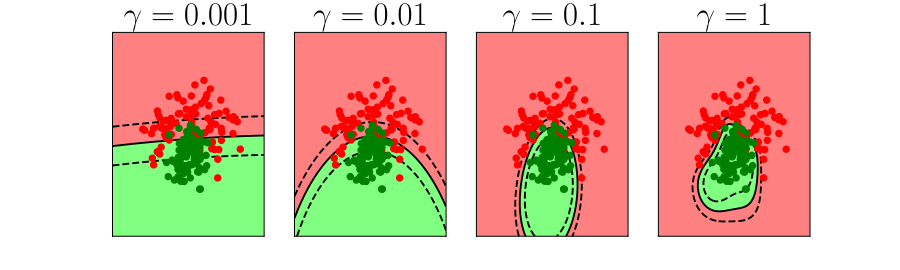
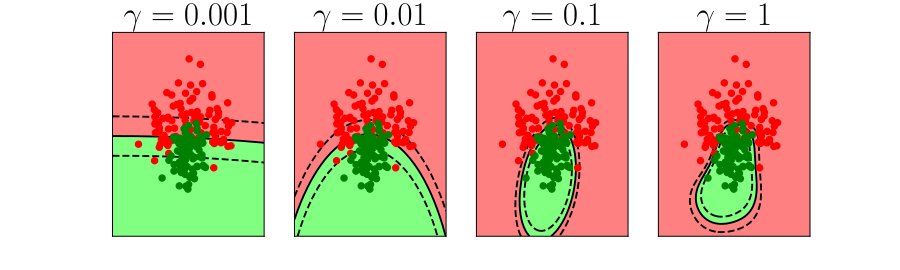
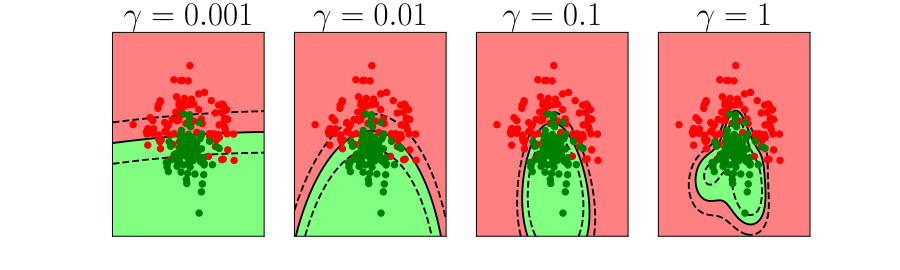
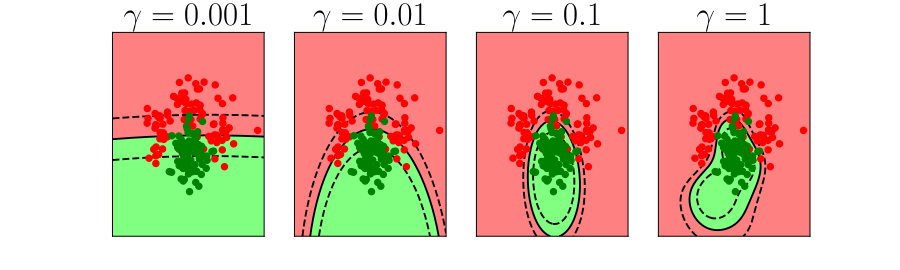
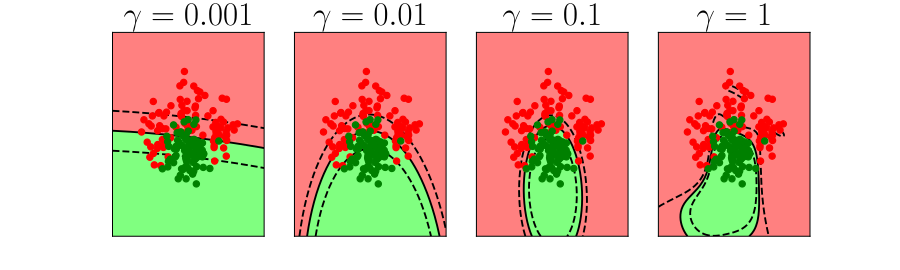
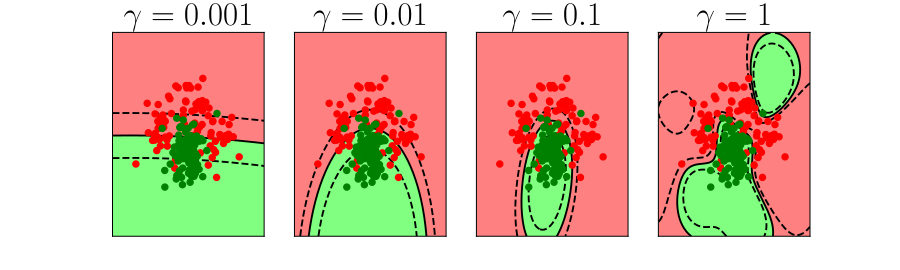
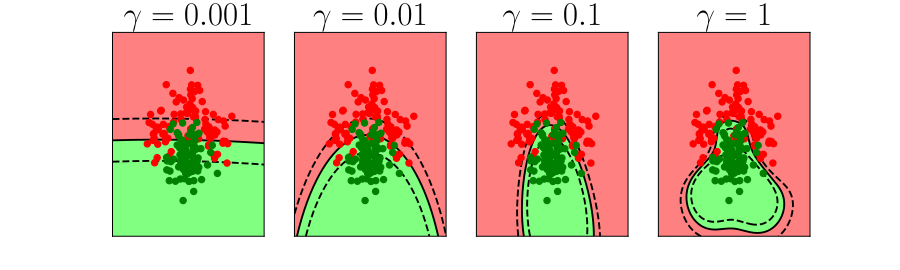
Further Reading
- Section 1.5 of Rogers and Girolami (2011)
Thanks!
twitter: @lawrennd
podcast: The Talking Machines
newspaper: Guardian Profile Page
blog posts: