Covariance Functions and Hyperparameter Optimization

GPy: A Gaussian Process Framework in Python

GPy: A Gaussian Process Framework in Python

• BSD Licensed software base.
• Wide availability of libraries, ‘modern’ scripting language.
• Allows us to set projects to undergraduates in Comp Sci that use GPs.
• Available through GitHub https://github.com/SheffieldML/GPy
• Reproducible Research with Jupyter Notebook.

Features

• Probabilistic-style programming (specify the model, not the algorithm).
• Non-Gaussian likelihoods.
• Multivariate outputs.
• Dimensionality reduction.
• Approximations for large data sets.

The Importance of the Covariance Function

$$\boldsymbol{ \mu}_f= \mathbf{A}^\top \mathbf{ y},$$

Improving the Numerics

In practice we shouldn’t be using matrix inverse directly to solve the GP system. One more stable way is to compute the Cholesky decomposition of the kernel matrix. The log determinant of the covariance can also be derived from the Cholesky decomposition.

Capacity Control

Gradients of the Likelihood

Overall Process Scale

Capacity Control and Data Fit

Learning Covariance Parameters

Can we determine covariance parameters from the data?

$$\mathcal{N}\left(\mathbf{ y}|\mathbf{0},\mathbf{K}\right)=\frac{1}{(2\pi)^\frac{n}{2}{\det{\mathbf{K}}^{\frac{1}{2}}}}{\exp\left(-\frac{\mathbf{ y}^{\top}\mathbf{K}^{-1}\mathbf{ y}}{2}\right)}$$

$$\begin{aligned} \mathcal{N}\left(\mathbf{ y}|\mathbf{0},\mathbf{K}\right)=\frac{1}{(2\pi)^\frac{n}{2}\color{yellow}{\det{\mathbf{K}}^{\frac{1}{2}}}}\color{cyan}{\exp\left(-\frac{\mathbf{ y}^{\top}\mathbf{K}^{-1}\mathbf{ y}}{2}\right)} \end{aligned}$$

$$\begin{aligned} \log \mathcal{N}\left(\mathbf{ y}|\mathbf{0},\mathbf{K}\right)=&\color{yellow}{-\frac{1}{2}\log\det{\mathbf{K}}}\color{cyan}{-\frac{\mathbf{ y}^{\top}\mathbf{K}^{-1}\mathbf{ y}}{2}} \\ &-\frac{n}{2}\log2\pi \end{aligned}$$

$$E(\boldsymbol{ \theta}) = \color{yellow}{\frac{1}{2}\log\det{\mathbf{K}}} + \color{cyan}{\frac{\mathbf{ y}^{\top}\mathbf{K}^{-1}\mathbf{ y}}{2}}$$

Capacity Control through the Determinant

The parameters are inside the covariance function (matrix). $$k_{i, j} = k(\mathbf{ x}_i, \mathbf{ x}_j; \boldsymbol{ \theta})$$

Eigendecomposition of Covariance

$$\mathbf{K}= \mathbf{R}\boldsymbol{ \Lambda}^2 \mathbf{R}^\top$$

$\boldsymbol{ \Lambda}$ represents distance on axes. $\mathbf{R}$ gives rotation.

Eigendecomposition of Covariance

• $\boldsymbol{ \Lambda}$ is diagonal, $\mathbf{R}^\top\mathbf{R}= \mathbf{I}$.
• Useful representation since $\det{\mathbf{K}} = \det{\boldsymbol{ \Lambda}^2} = \det{\boldsymbol{ \Lambda}}^2$.

Capacity control: $\color{yellow}{\log \det{\mathbf{K}}}$

❮ ❯

Quadratic Data Fit

Data Fit: $\color{cyan}{\frac{\mathbf{ y}^\top\mathbf{K}^{-1}\mathbf{ y}}{2}}$

❮ ❯

$$E(\boldsymbol{ \theta}) = \color{yellow}{\frac{1}{2}\log\det{\mathbf{K}}}+\color{cyan}{\frac{\mathbf{ y}^{\top}\mathbf{K}^{-1}\mathbf{ y}}{2}}$$

Data Fit Term

❮ ❯

Exponentiated Quadratic Covariance

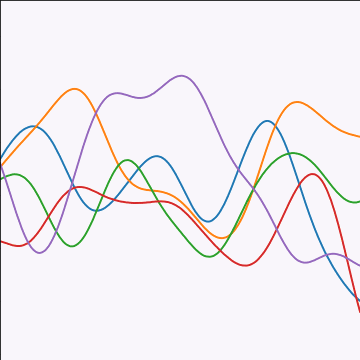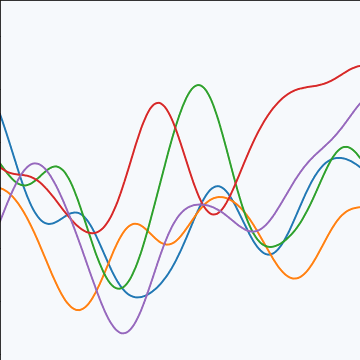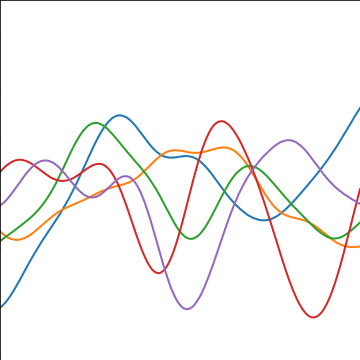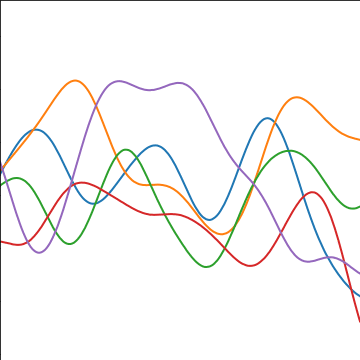
Where Did This Covariance Matrix Come From?

$$k(\mathbf{ x}, \mathbf{ x}^\prime) = \alpha \exp\left(-\frac{\left\Vert \mathbf{ x}- \mathbf{ x}^\prime\right\Vert^2_2}{2\ell^2}\right)$$

Computing Covariance

❮ ❯

Computing Covariance

❮ ❯

Computing Covariance

❮ ❯

Brownian Covariance

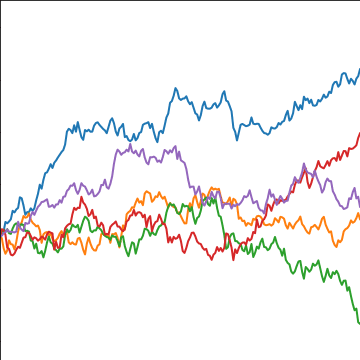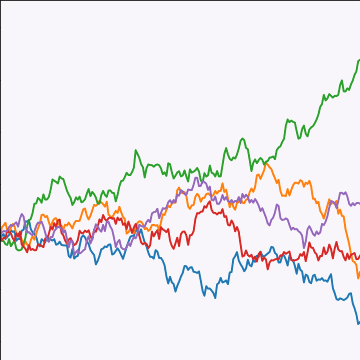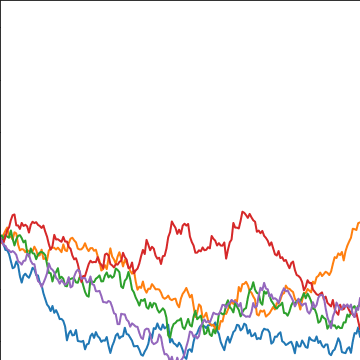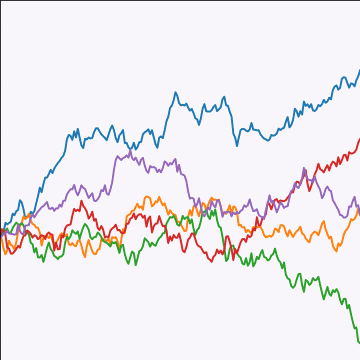
Where did this covariance matrix come from?

Markov Process

Visualization of inverse covariance (precision).

• Precision matrix is sparse: only neighbours in matrix are non-zero.

• This reflects conditional independencies in data.

• In this case Markov structure.

Where did this covariance matrix come from?

Exponentiated Quadratic

Visualization of inverse covariance (precision).

Covariance Functions

Markov Process

Visualization of inverse covariance (precision).

Exponential Covariance

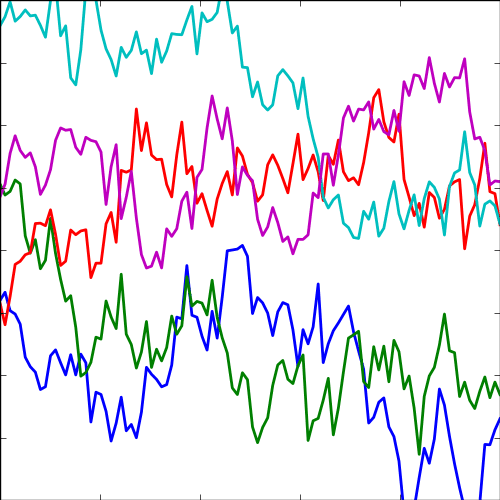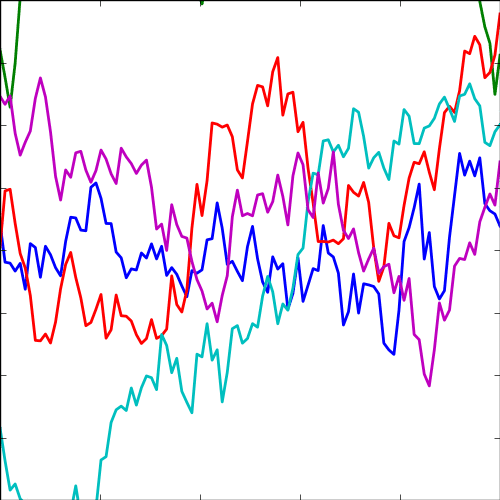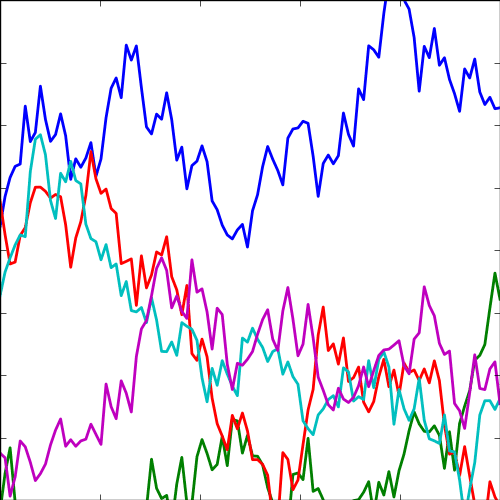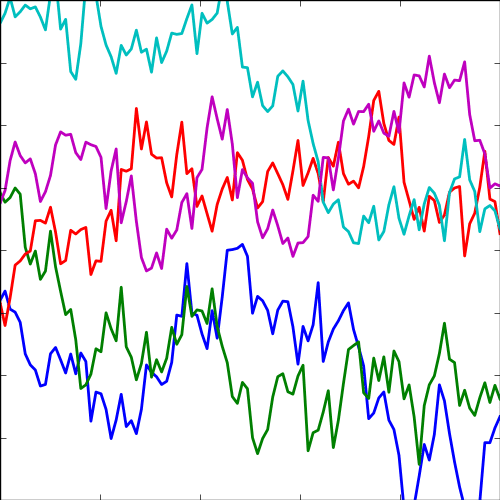
Basis Function Covariance

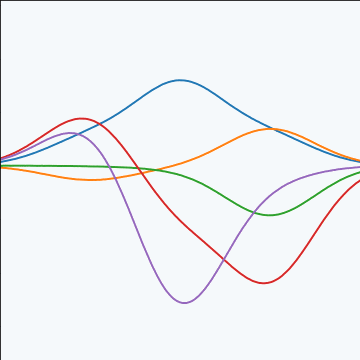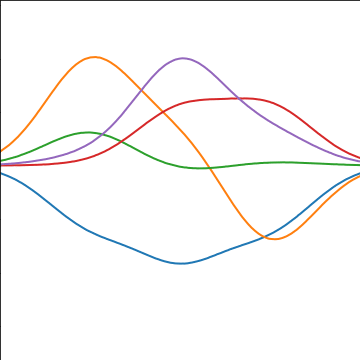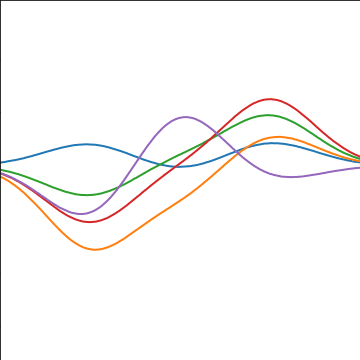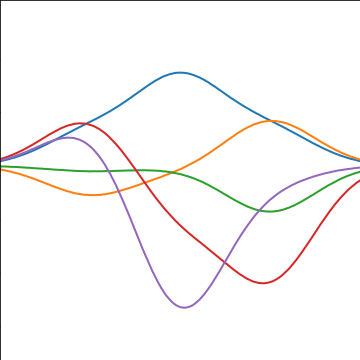
Degenerate Covariance Functions

RBF Basis Functions

$$\phi_k(x) = \exp\left(-\frac{\left\Vert x-\mu_k \right\Vert_2^{2}}{\ell^{2}}\right).$$

$$\boldsymbol{ \mu}= \begin{bmatrix} -1 \\ 0 \\ 1\end{bmatrix},$$

$$k\left(\mathbf{ x},\mathbf{ x}^{\prime}\right)=\alpha\boldsymbol{ \phi}(\mathbf{ x})^\top \boldsymbol{ \phi}(\mathbf{ x}^\prime).$$

Bochners Theoerem

Given a positive finite Borel measure $\mu$ on the real line $\mathbb{R}$, the Fourier transform $Q$ of $\mu$ is the continuous function $$Q(t) = \int_{\mathbb{R}} e^{-itx} \text{d} \mu(x).$$ $Q$ is continuous since for a fixed $x$, the function $e^{-itx}$ is continuous and periodic. The function $Q$ is a positive definite function, i.e. the kernel $k(x, x^\prime)= Q(x^\prime - x)$ is positive definite.

Bochner’s theorem (Bochner, 1959) says the converse is true, i.e. every positive definite function $Q$ is the Fourier transform of a positive finite Borel measure. A proof can be sketched as follows (Stein, 1999)

$$f(\mathbf{ x}) = \sum_{i=1}^ny_i \delta(\mathbf{ x}-\mathbf{ x}_i),$$

$$F(\boldsymbol{\omega}) = \int_{-\infty}^\infty f(\mathbf{ x}) \exp\left(-i2\pi \boldsymbol{\omega}^\top \mathbf{ x}\right) \text{d} \mathbf{ x}$$

$$F(\boldsymbol{\omega}) = \sum_{i=1}^ny_i\exp\left(-i 2\pi \boldsymbol{\omega}^\top \mathbf{ x}_i\right)$$

$$F(\omega) = \int_{-\infty}^\infty f(t) \left[\cos(2\pi \omega t) - i \sin(2\pi \omega t) \right]\text{d} t$$

$$\exp(ix) = \cos x + i\sin x$$ we can re-express this form as $$F(\omega) = \int_{-\infty}^\infty f(t) \exp(-i 2\pi\omega)\text{d} t$$

$$f(t) = \int_{-\infty}^\infty F(\omega) \exp(2\pi\omega)\text{d} \omega.$$

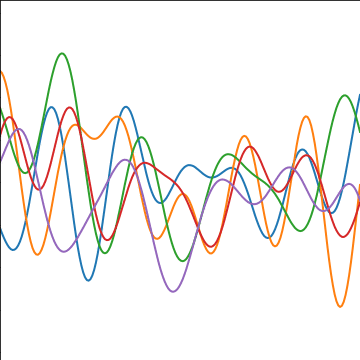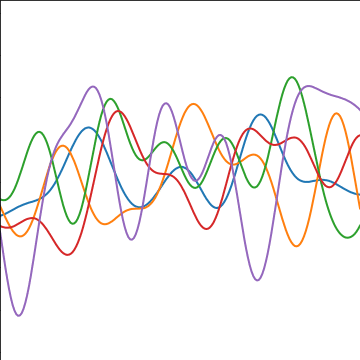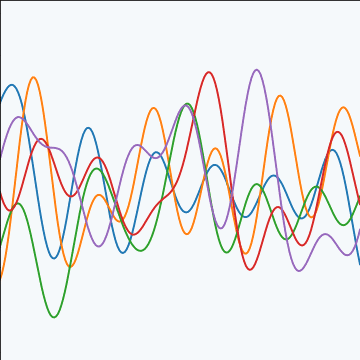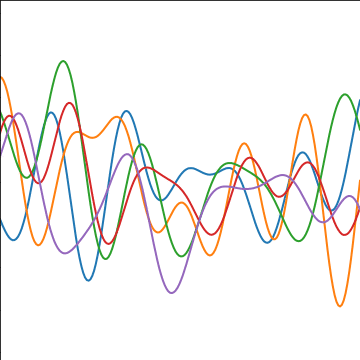
Sinc Covariance

Matérn 3/2 Covariance

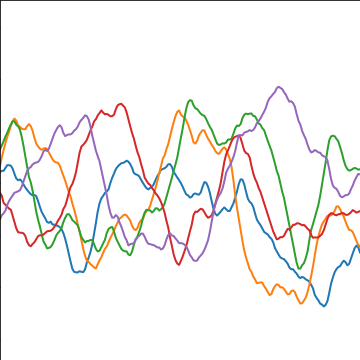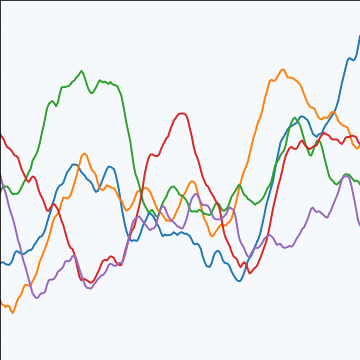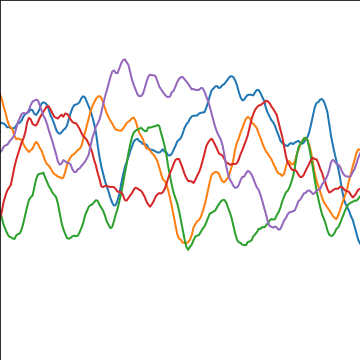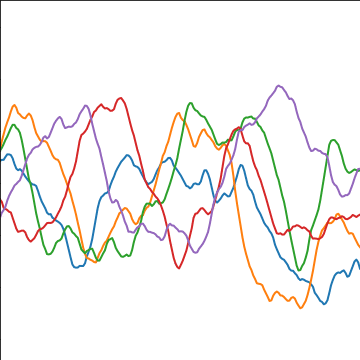
Matérn 5/2 Covariance

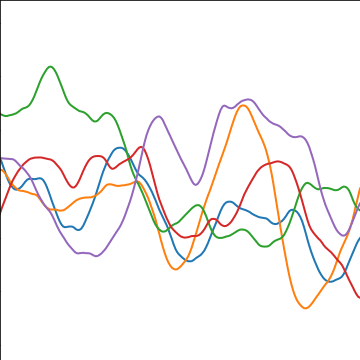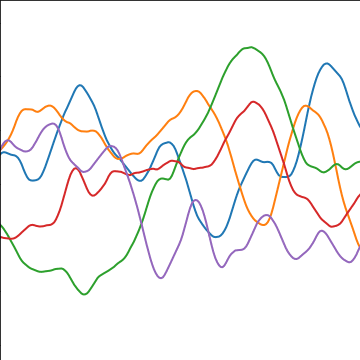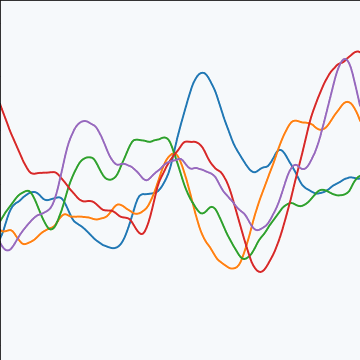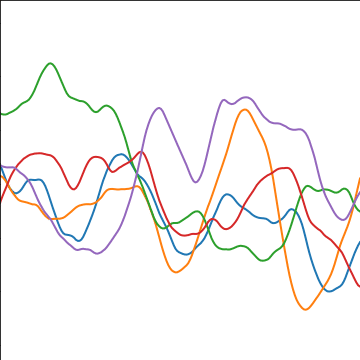
Rational Quadratic Covariance

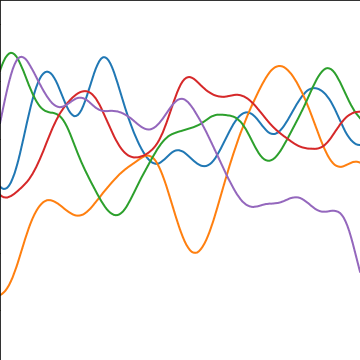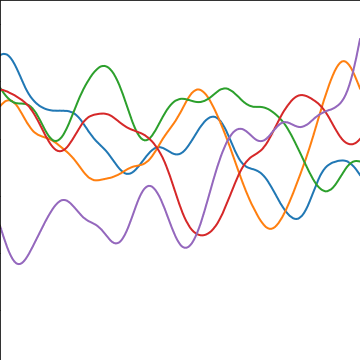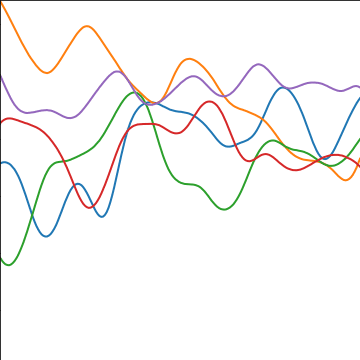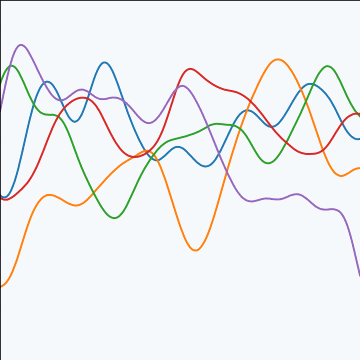
Polynomial Covariance

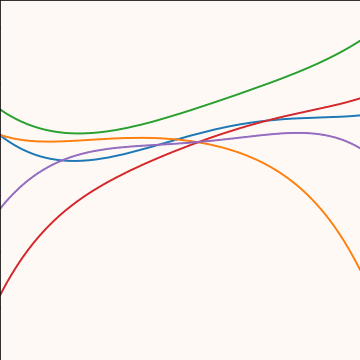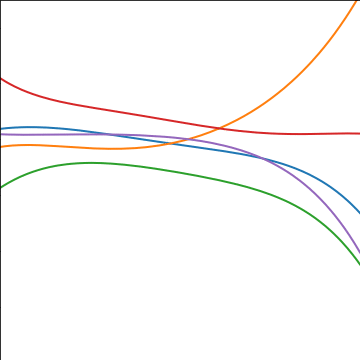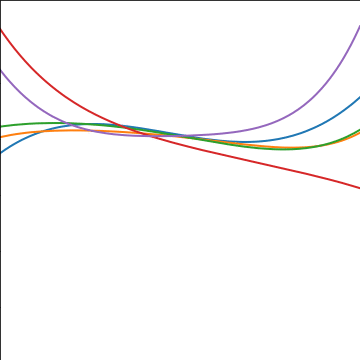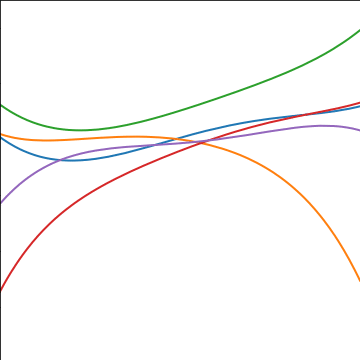
Periodic Covariance

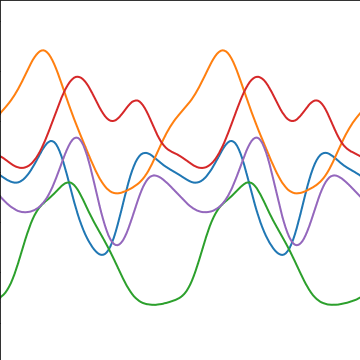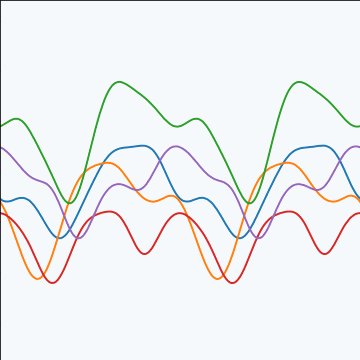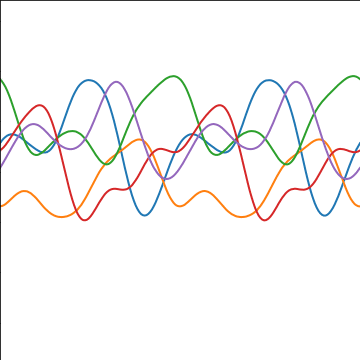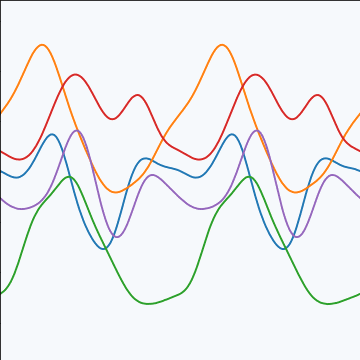
MLP Covariance

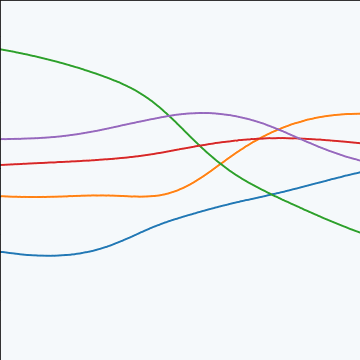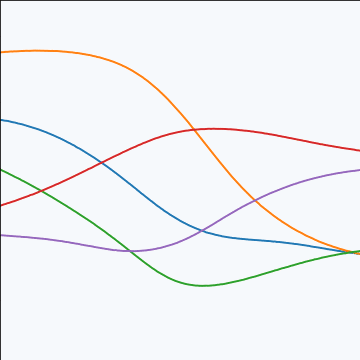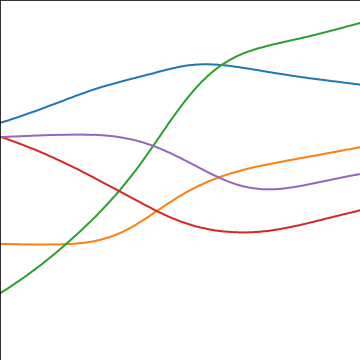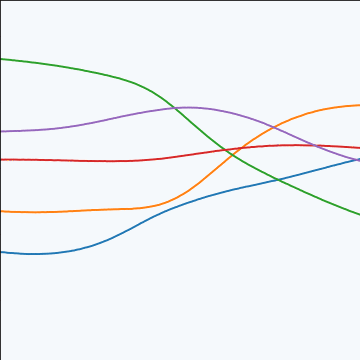
RELU Covariance

Additive Covariance

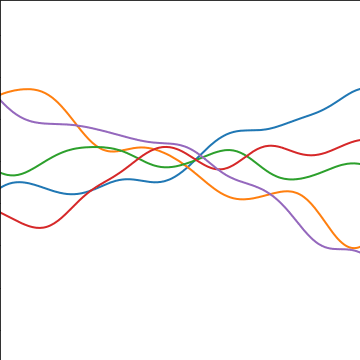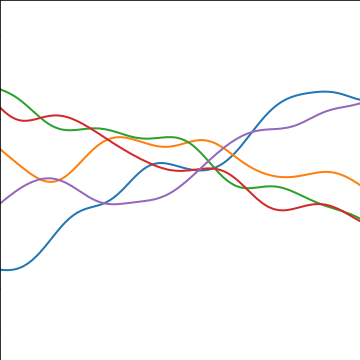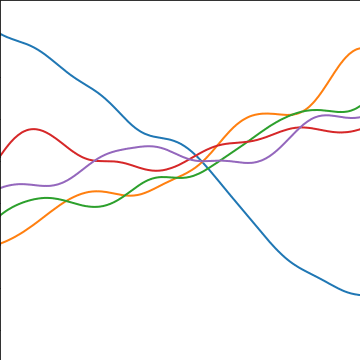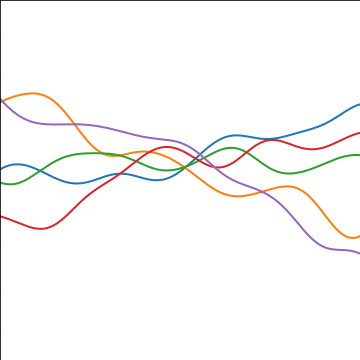
Product Covariance

Mauna Loa Data

Mauna Loa Data

Mauna Loa Test Data

Gaussian Process Fit

Mauna Loa Data GP

Box Jenkins Airline Passenger Data

Mauna Loa Data

Gaussian Process Fit

Box-Jenkins Airline PassengerData GP

Spectral Mixture Kernel

Box-Jenkins Airline Spectral Mixture

Mauna Loa Spectral Mixture